小学数学精讲教案4_2_5 平移、旋转、割补 教师版 11页

‎4-2-5.平移、旋转、割补 例题精讲 图形变换，是指不改变图形的大小、形状，只通过位置关系的改变（旋转、平移、折叠等），构成新的图形．‎ 【例 1】 右图是一块长方形草地，长方形的长是16，宽是10．中间有两条道路，一条是长方形，一条是平行四边形，它们的宽都是2，求草地部分的面积（阴影部分）有多大？‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】2星 【题型】解答 【解析】 如图所示，将道路平移后的。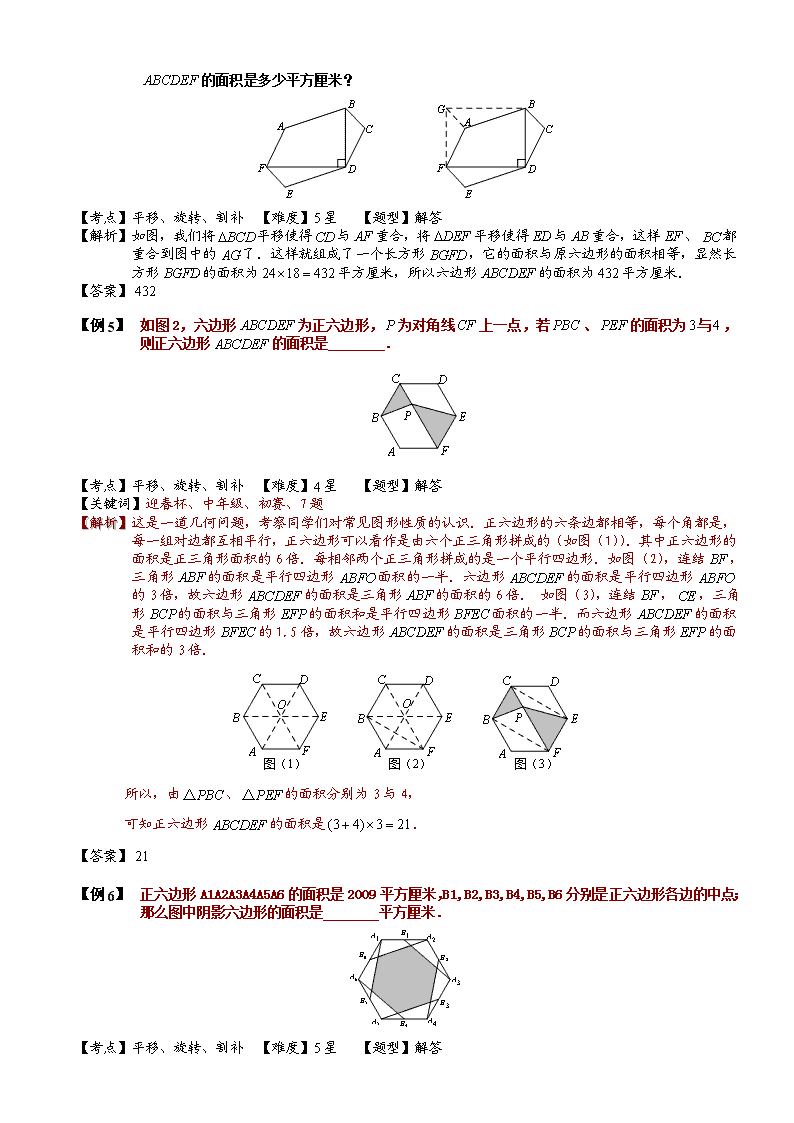‎ ‎【答案】‎ 【例 2】 如图所示，一个正十二边形的边长是‎1厘米，空白部分是等边三角形，一共有12个．请算出阴影部分的面积．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如图，将阴影部分分割成一个正六边形和12个小三角形，再把正六边形分割成6个正三角形，由于正十二边形的每个内角为，所以阴影小三角形的顶角等于，每个顶角的两边和与其相邻的正三角形的底边所成的角都是，所以通过如右上图所示的平移可以组成6个边长为‎1厘米的正方形，所以所求阴影部分面积为平方厘米．‎ ‎【答案】‎ 【例 3】 如图所示，梯形中，平行于，又，，．试求梯形 的面积．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如右图，将沿平移至,连接,在三角形中，有，，，有，所以三角形为直角三角形．‎ 由于，所以梯形的面积与三角形的面积相等，为．‎ ‎【答案】‎ 【例 4】 如下图，六边形中，，，，且有平行于，平行于，平行于，对角线垂直于，已知厘米，厘米，请问六边形 的面积是多少平方厘米？‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图，我们将平移使得与重合，将平移使得与重合，这样、都重合到图中的了．这样就组成了一个长方形，它的面积与原六边形的面积相等，显然长方形的面积为平方厘米，所以六边形的面积为平方厘米．‎ ‎【答案】‎ 【例 2】 如图2，六边形为正六边形，为对角线上一点，若、的面积为与，则正六边形的面积是　　　　．‎ ‎【考点】平移、旋转、割补 【难度】4星 【题型】解答 ‎【关键词】迎春杯、中年级、初赛、7题 【解析】 这是一道几何问题，考察同学们对常见图形性质的认识．正六边形的六条边都相等，每个角都是，每一组对边都互相平行，正六边形可以看作是由六个正三角形拼成的（如图（1））．其中正六边形的面积是正三角形面积的6倍．每相邻两个正三角形拼成的是一个平行四边形．如图（2），连结，三角形的面积是平行四边形面积的一半．六边形的面积是平行四边形的3倍，故六边形的面积是三角形的面积的6倍． 如图（3），连结，，三角形的面积与三角形的面积和是平行四边形面积的一半．而六边形的面积是平行四边形的1.5倍，故六边形的面积是三角形的面积与三角形的面积和的3倍．‎ 所以，由、的面积分别为3与4，‎ 可知正六边形的面积是．‎ ‎【答案】‎ 【例 3】 正六边形A‎1A2A3A4A5A6的面积是2009平方厘米，B1,B2,B3,B4,B5,B6分别是正六边形各边的中点；那么图中阴影六边形的面积是　　　　平方厘米．‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 ‎【关键词】迎春杯、六年级、初赛、14题 【解析】 如图，设与的交点为，则图中空白部分由个与一样大小的三角形组成，只要求出了的面积，就可以求出空白部分面积，进而求出阴影部分面积.‎ 连接、、 设的面积为“”，则面积为“”，面积为“”，那么面积为的倍，为“”，梯形的面积为，的面积为“”，的面积为 根据蝴蝶定理，，故，‎ 所以，即的面积为梯形面积的，故为六边形面积的，那么空白部分的面积为正六边形面积的，所以阴影部分面积为(平方厘米).‎ ‎【答案】‎ 【例 1】 按照图中的样子，在一平行四边形纸片上割去了甲、乙两个直角三角形．已知甲三角形两条直角边分别为和，乙三角形两条直角边分别为和，求图中阴影部分的面积．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如右图，我们将三角形甲与乙进行平移，就会发现平行四边形面积等于平移后两个长方形面积之和．所以阴影部分面积为：‎ ‎【答案】‎ 【例 2】 在一个等腰三角形中，两条与底边平行的线段将三角形的两条边等分成三段(见右图)，求图中阴影部分的面积占整个图形面积的几分之几.‎ ‎【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 阴影总值是一个梯形.我们用三种方法解答.‎ ‎⑴ 割补法 从顶点作底边上的高，得到两个相同的直角三角形.将这两个直角三角形拼成一个长方形(见下图).显然，阴影部分正好是长方形的，所以原题阴影部分占整个图形面积的.‎ ‎⑵ 拼补法 将两个这样的三角形拼成一个平行四边形(下页左上图).显然，图中阴影面积占平行四边形面积的.根据商不变性质，将阴影面积和平行四边形面积同时除以，商不变.所以原题阴影部分占整个图形面积的.‎ ‎⑶ 等分法 将原图等分成个小三角形(见右上图)，阴影部分占个小三角形，所以阴影部分占整个图形面积的.‎ 注意，后两种方法对任意三角形都适用.也就是说，将例题中的等腰三角形换成任意三角形，其它条件不变，结论仍然成立.‎ ‎【答案】‎ 【例 1】 如下左图，有两个大小相同的完全重叠在一起的正方形，现在以点为中心转动一个正方形．当厘米，厘米，厘米时(如下右图)，求右图中的两个正方形相重叠部分的面积(注意，图的尺寸不一定准确)．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 右图由左图旋转而得，则右图中的8个空白小三角形都是完全相同的，右图中重叠部分的面积等于正方形面积减去4个小三角形的面积，从右图中可以看出正方形的边长为厘米，所以重叠部分的面积为：(平方厘米)．‎ ‎【答案】‎ 【例 2】 如图，在直角三角形中有一个正方形，已知厘米，厘米，求阴影部分的面积．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 绕点逆时针旋转，使与重合，则点落在边上的点处，且．则阴影部分面积转化为直角三角形的面积，所以阴影部分的面积为平方厘米．‎ ‎【答案】‎ 【例 3】 四边形ABCD中,AB=30,AD=48,BC=14,CD=40.又已知∠ABD+∠BDC=900,求四边形ABCD的面积．‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图,以BD的垂直平分线为对称轴L,做△ABD关于L的对称图形△BD.连接C．‎ 因为∠ABD+∠BDC=9000而∠ABD=∠DB=900,所以有∠DB+∠BDC=900．‎ 那么CD为直角三角形,由勾股定理知=2500,所以.‎ 而在△BC中,有B=AD=48,有482+142=2500,即B2+BC2=C2,即△BC为直角三角形．‎ 有.‎ 而|.‎ 评注:Ⅰ.本题以∠ABC+∠BDC=900突破口,通过对称变换构造出与原图形相关的角三角形 Ⅱ.对于这道题我们还可以将△BCD作L的对称图形.如下：‎ ‎【答案】‎ 【例 1】 如图,在三角形ABD中,当AB和CD的长度相等时,请求出“?”所示的角是多少度,给出过程．‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为AB=CD,于是可以将三角形ABC的边BA边与CD对齐,如下图． 在下图中有∠BCA=110°,所以∠ACD=70°于是∠=∠+∠=∠+∠=70°+40°=110°；‎ 即∠=110°=∠；又因为只是移动的变化,所以=；则是一等腰梯形．于是,∠=180°110°=70°；又∠=30°,所以∠=70°30°=40°.‎ ‎【答案】°‎ 【例 1】 如图所示的四边形的面积等于多少？‎ ‎【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 题目中要求的四边形既不是正方形也不是长方形，难以运用公式直接求面积.‎ 我们可以利用旋转的方法对图形实施变换：‎ 把三角形绕顶点逆时针旋转，使长为的两条边重合，此时三角形将旋转到三角形 的位置.这样，通过旋转后所得到的新图形是一个边长为的正方形，且这个正方形的面积就是原来四边形的面积.‎ 因此，原来四边形的面积为.(也可以用勾股定理)‎ ‎【答案】‎ 【例 2】 如图，三角形是等腰直角三角形，是三角形外的一点，其中，，求四边形的面积．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为和都是直角，和为，所以和的和也为，可以旋转三角形，使和重合，则四边形的面积转化为等腰直角三角形，面积为平方厘米．‎ ‎【答案】‎ 【例 3】 如图所示，中，，，，以为一边向外作正方形，中心为，求的面积．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 ‎【关键词】武汉明心奥数 【解析】 如图，将沿着点顺时针旋转，到达的位置．‎ 由于，，所以．而，‎ 所以，那么、、三点在一条直线上．‎ 由于，，所以是等腰直角三角形，且斜边为，所以它的面积为．根据面积比例模型，的面积为．‎ ‎【答案】‎ 【例 4】 如图，直角梯形中，，，，，将腰以为中心逆时针旋转至 ‎，连接、，则的面积是 ．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 ‎【关键词】武汉明心奥数 【解析】 如图所示，将以为中心顺时针旋转，到的位置．延长与交于．‎ 由于是直角梯形，与垂直，则四边形是长方形，则．‎ 由于与面积相等，而的底边，高，所以的面积为，那么的面积也为1．‎ ‎【答案】‎ 【例 2】 如图，正方形和有一个公共点，试比较三角形和三角形的面积．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为和是直角，所以和是互补角，将三角形顺时针旋转到达的位置，则、、在同一条直线上，且，即是的中点，所以三角形和三角形面积相等，则三角形和三角形面积相等．‎ ‎【答案】相等 【例 3】 如图，以正方形的边为斜边在正方形内作直角三角形，，、交于．已知、的长分别为、，求三角形的面积．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 ‎【关键词】资优杯 【解析】 如图，连接，以点为中心，将顺时针旋转到的位置．‎ 那么，而也是，所以四边形是直角梯形，且，‎ 所以梯形的面积为：‎ ‎()．‎ 又因为是直角三角形，根据勾股定理，，所以()．‎ 那么()，‎ 所以()．‎ ‎【答案】‎ 【例 1】 如图，已知，，，，则 ‎ ．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 ‎【关键词】迎春杯、高年级、复赛、10题 【解析】 将三角形绕点和点分别顺时针和逆时针旋转，构成三角形和，再连接，显然，，，所以是正方形．三角形和三角形关于正方形的中心中心对称，在中心对称图形中有如下等量关系：‎ ‎；；．‎ 所以．‎ ‎【答案】‎ 【例 2】 如图所示的四边形中，，，厘米，连接对角线，．求四边形的面积．‎ ‎【考点】平移、旋转、割补 【难度】4星 【题型】解答 ‎【关键词】第八届、华杯总决赛 【解析】 由，，可得，．‎ 将剪下来，翻转，再贴在边上，即将点粘在点上，点粘在点上，如右上图所示．则点在点的位置．由于，所以、、三点在同一条直线上．由于，所以，即是等腰直角三角形，它的面积就等于四边形的面积，所以四边形的面积为平方厘米．‎ ‎【答案】‎ 【例 3】 如图，在中，，求“？”的度数．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图，由于，可以将移动到，由于，，所以，又，而，所以四边形是等腰梯形，有，．‎ 点评：通过构造全等三角形来转化．‎ ‎【答案】°‎ 【例 1】 下图三角形是等腰三角形，，．三角形是正三角形，点在 边上，．当三角形的面积是时，三角形的面积是多少？‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 以点为中心，由三个三角形可拼成右图：连结、、，则是一个正六边形．连结、、，显然是一个等边三角形，并且它的面积是正六边形面积的一半，所以是三角形的面积的3倍．‎ 由于，根据“鸟头定理”，，‎ 所以，则．‎ ‎【答案】‎ 【例 2】 如图，正方形有三个顶点分别在的三条边上，．求正方形的面积．‎ ‎【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图，我们设的面积为1，有，‎ 所以，， 所以．‎ ‎ ‎ 如下图左，将三角形和三角形分别以、为中心按箭头方向旋转，形成由两个直角三角形连在一起的一个四边形，如下图右，、、被虚线分成两个直角三角形，它们的面积之和为：，所以．‎ ‎ ‎ ‎【答案】‎ 【例 3】 如下图,△ABC是边长为1的等边三角形,△BCD是等腰三角形BD=CD，顶角∠BDC=1200,∠MDN=600,求△AMN的周长.‎ ‎【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 如下图, 延长AC至P,使CP=MB,连接DP.‎ 则有∠MBD=600+∠PCD；CP=BM；BD=CD,‎ 所以有△MBD≌△PCD.于是∠MDC=∠PDC；‎ 又因为∠MDB+∠NDC=600,所以∠PDC+∠NDC=∠NDP=600；‎ MD=PD,在△MDN、△PND中,∠NDM=∠NDP,ND=ND,MD=PD,‎ 于是△MND≌△PND.有MN=PN.因为NP=NP=NC+CP,而AM=AB-MB=AB-CP,‎ 所以AM+AN+MN=(AB-CP)+AN+(NC+CP)=AB+AN+NC=2.即△AMN的周长为2.‎ ‎【答案】‎ 【例 1】 若干个大小相同的正五边形如右图排成环状，下图中所示的只是3个五边形．那么要完成这一圈共需 ‎　 个正五边形．‎ ‎ ‎ ‎【考点】平移、旋转、割补 【难度】4星 【题型】解答 ‎【关键词】迎春杯、六年级、初赛、5题 【解析】 如图，设为圆心，、、、为五边形的顶点，连接、、.‎ 从图中可以看出，和是完全相同的，所以，又五边形内角和为，所以正五边形的每个内角都为，即， 那么，则， 又，所以 所以要用个正五边形才能围成一圈.‎ ‎【答案】‎ 【例 1】 如图，ABCD是矩形，BC=‎6cm, AB=‎10cm,AC和BD是对角线，图中的阴影部分以C为轴旋转一周，则阴影部分扫过的立体的体积是多少立方厘米？（π取3.14）‎ ‎【考点】平移、旋转、割补 【难度】3星 【题型】解答 ‎【关键词】华杯赛、决赛、第11题 【解析】 ‎①设三角形BCO以CD为轴旋转一周所得到的立体的体积是s，S等于高为‎10厘米，底面半径是‎6厘米的圆锥的体积减去2个高为‎5厘米，底面半径是‎3厘米的圆锥的体积。 ②即：，2S＝180π＝565.2（立方厘米）‎ 体积是565.2立方厘米。‎ ‎【答案】‎ 【例 2】 一个半径为‎1厘米的圆盘沿着一个半径为‎4厘米的圆盘外侧做无滑动的滚动，当小圆盘的中心围绕大圆盘中心转动90度后（如图2），小圆盘运动过程中扫出的面积是（　）平方厘米。（=3.14）‎ ‎【考点】平移、旋转、割补 【难度】3星 【题型】解答 ‎【关键词】华杯赛、决赛、第4题、10分 【解析】 ‎18.84‎ ‎【答案】18.84‎