2018届八年级数学下册第十九章一次函数-函数的图象第2课时函数的表示方法同步练习 4页

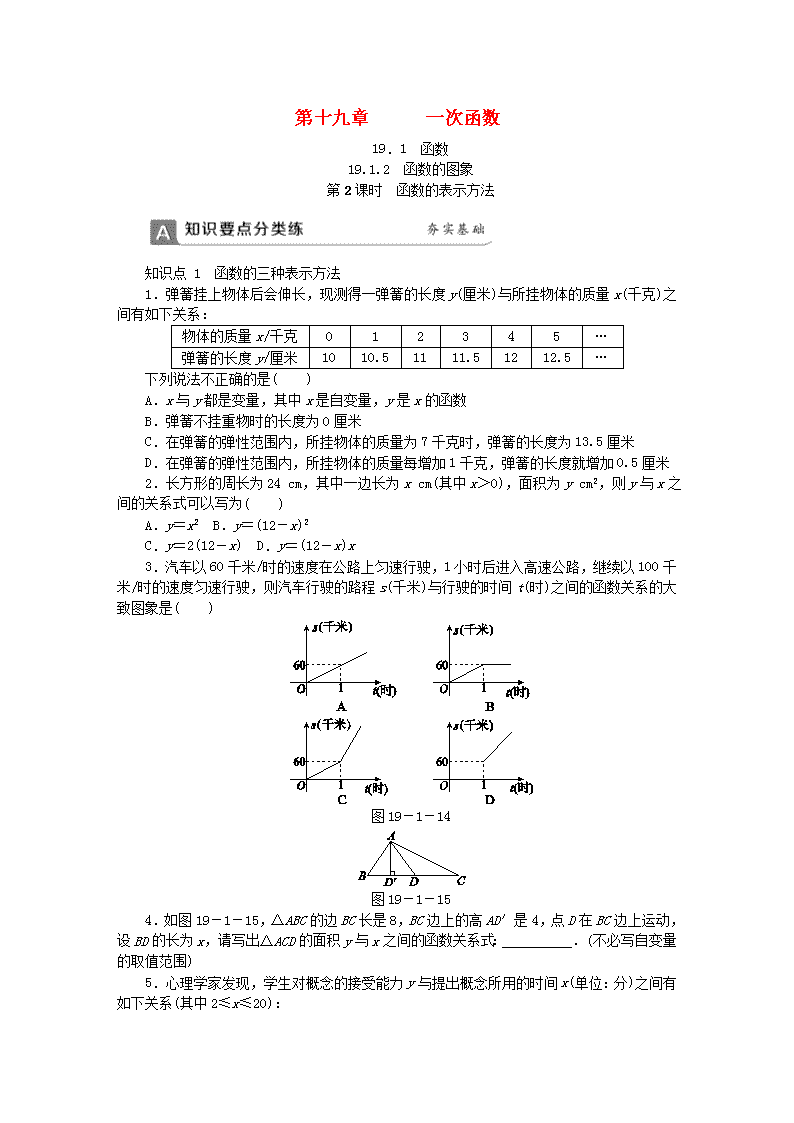
第十九章　一次函数19．1　函数19.1.2　函数的图象第2课时　函数的表示方法知识点1　函数的三种表示方法1．弹簧挂上物体后会伸长，现测得一弹簧的长度y(厘米)与所挂物体的质量x(千克)之间有如下关系：物体的质量x/千克012345…弹簧的长度y/厘米1010.51111.51212.5…下列说法不正确的是(　　)A．x与y都是变量，其中x是自变量，y是x的函数B．弹簧不挂重物时的长度为0厘米C．在弹簧的弹性范围内，所挂物体的质量为7千克时，弹簧的长度为13.5厘米D．在弹簧的弹性范围内，所挂物体的质量每增加1千克，弹簧的长度就增加0.5厘米2．长方形的周长为24cm，其中一边长为xcm(其中x＞0)，面积为ycm2，则y与x之间的关系式可以写为(　　)A．y＝x2B．y＝(12－x)2C．y＝2(12－x)D．y＝(12－x)x3．汽车以60千米/时的速度在公路上匀速行驶，1小时后进入高速公路，继续以100千米/时的速度匀速行驶，则汽车行驶的路程s(千米)与行驶的时间t(时)之间的函数关系的大致图象是(　　)图19－1－14图19－1－154．如图19－1－15，△ABC的边BC长是8，BC边上的高AD′是4，点D在BC边上运动，设BD的长为x，请写出△ACD的面积y与x之间的函数关系式：__________．(不必写自变量的取值范围)5．心理学家发现，学生对概念的接受能力y与提出概念所用的时间x(单位：分)之间有如下关系(其中2≤x≤20)：n提出概念所用时间(x)257101213141720对概念的接受能力(y)47.853.556.35959.859.959.858.355(1)上表中反映了哪两个变量之间的关系？(2)当提出概念所用时间是10分钟时，学生的接受能力是多少？(3)根据表格中的数据，你认为提出概念几分钟时，学生对概念的接受能力最强；(4)从表中可知，当时间x在什么范围内时，学生的接受能力逐步增强？当时间x在什么范围内时，学生的接受能力逐步降低？知识点2　函数三种表示方法的综合应用6．下表是一项试验的统计数据，表示皮球下落时的开始高度d与弹跳高度b的关系．d(cm)5080100150b(cm)25405075则弹跳高度b与开始高度d的函数解析式是(　　)A．b＝d2B．b＝2dC．b＝D．b＝d＋257．声音在空气中传播的速度(简称“声速”)和气温有下表中的关系：气温(℃)05101520声速(m/s)331334337340343(1)上表反映了________之间的关系，其中______是自变量，________是________的函数；(2)若用T(℃)表示气温，v(m/s)表示声速，则随着T的增大，v将发生怎样的变化？(3)根据表中数据的变化，你发现了什么规律？写出v与T之间的函数解析式(不需要写自变量的取值范围)；(4)根据你发现的规律，回答下列问题：在30℃发生闪电的夏夜，小明在看到闪电6s后听到雷声，那么发生打雷的地方距小明大约有多远？8．八(1)班同学在探究弹簧的长度与砝码质量的关系时，通过试验得到的相应数据如下表所示：n砝码质量x/克050100150200250300400500弹簧长度y/厘米2345677.57.57.5则y关于x的函数图象是图19－1－16中的(　　)图19－1－169．甲、乙两车分别从A，B两地同时相向匀速行驶，当乙车到达A地后，继续保持原速向远离B的方向行驶，而甲车到达B地后立即掉头，并保持原速与乙车同向行驶，经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计)．设两车行驶的时间为x(时)，两车之间的距离为y(千米)，y与x之间的函数关系如图19－1－17所示，则当甲车到达B地时，乙车距A地________千米．图19－1－17　　图19－1－1810．一个装有进水管和出水管的容器，从某一时刻起只打开进水管进水，经过一段时间，再打开出水管放水，至12分钟时，关闭进水管．在打开进水管到关闭进水管这段时间内，容器内的水量y(单位：升)与时间x(单位：分)之间的函数关系如图19－1－18所示，关闭进水管后，经过________分钟，容器中的水恰好放完．11．一辆汽车由A地驶向相距240千米的B地，它的平均速度为30千米/时，求汽车距B地的路程s(千米)与行驶时间t(时)之间的函数解析式，并画出这个函数图象．12．某城市居民用水实行阶梯收费，每户每月用水量如果未超过20吨，按每吨2.5元收费，如果超过20吨，未超过的部分按每吨2.5元收费，超过的部分按每吨3.3元收费．设某户每月用水量为x吨，应缴水费为y元．n(1)分别写出每月用水量未超过20吨和超过20吨时，y与x之间的函数解析式；(2)若该城市某户4月份的水费平均每吨2.8元，求该户4月份用水多少吨．