贵阳专版2019届中考数学总复习阶段测评4图形的性质 5页

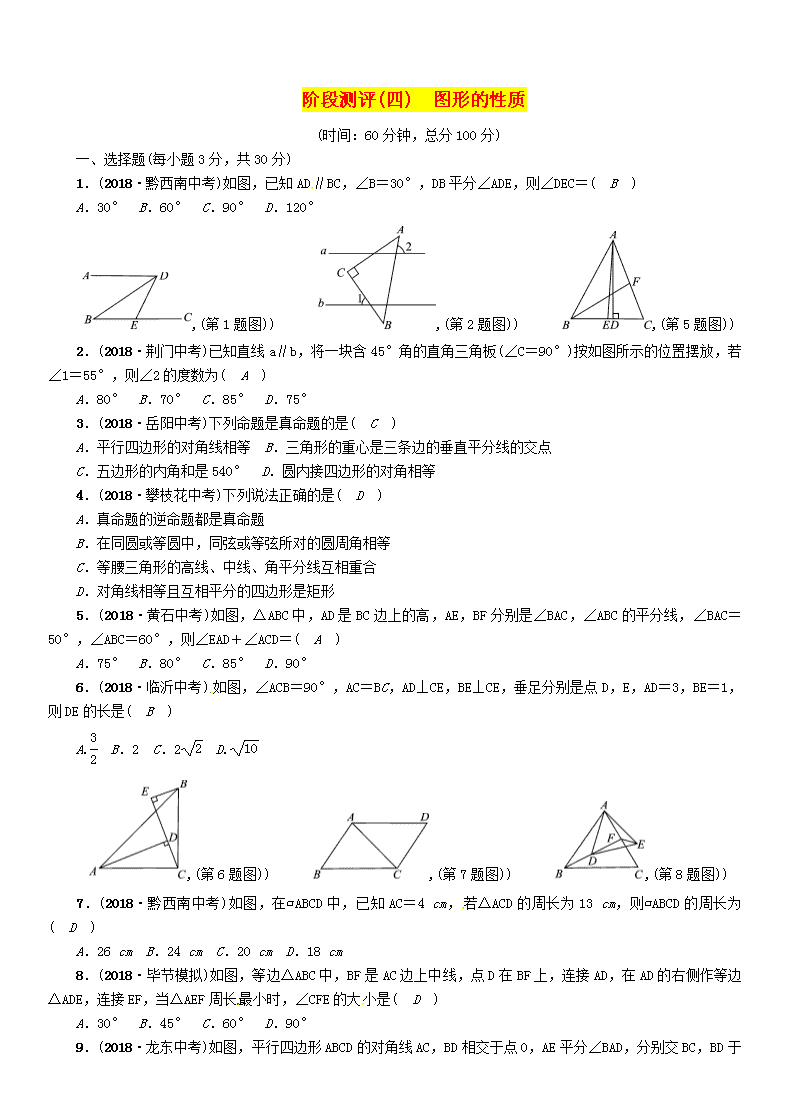
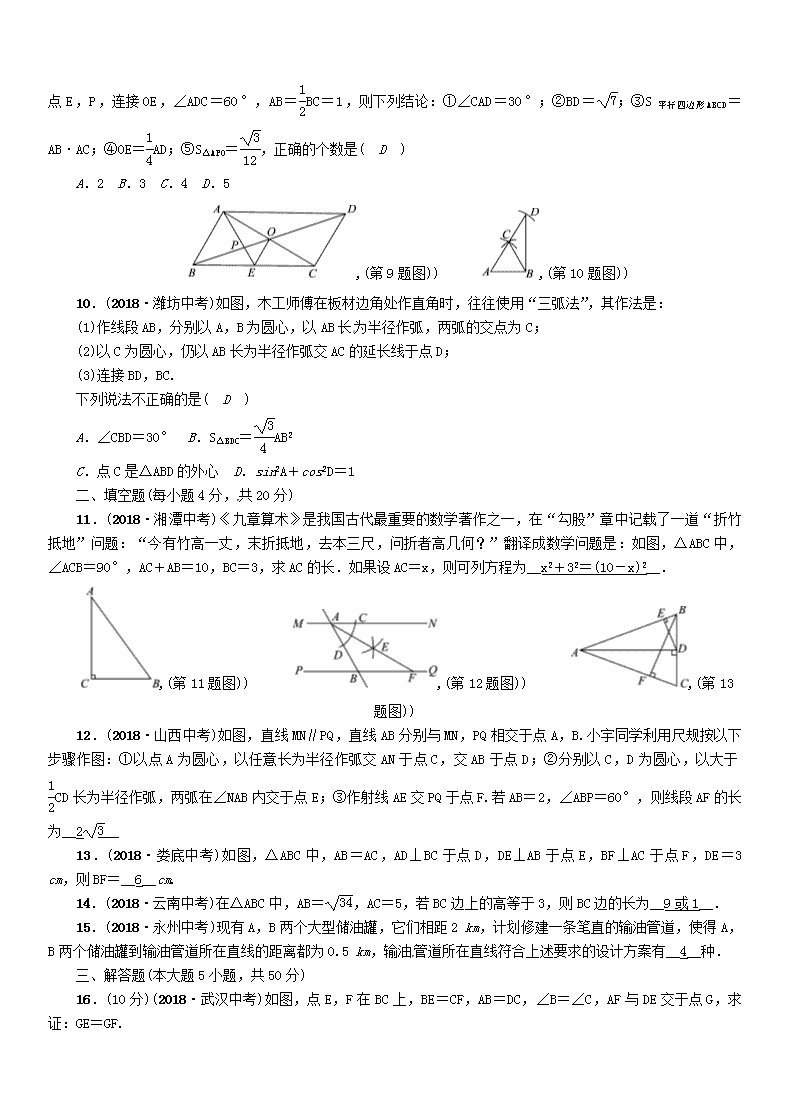
阶段测评(四)　图形的性质(时间：60分钟，总分100分)一、选择题(每小题3分，共30分)1．(2018·黔西南中考)如图，已知AD∥BC，∠B＝30°，DB平分∠ADE，则∠DEC＝(　B　)A．30°B．60°C．90°D．120°,(第1题图))　　　,(第2题图))　　　,(第5题图))2．(2018·荆门中考)已知直线a∥b，将一块含45°角的直角三角板(∠C＝90°)按如图所示的位置摆放，若∠1＝55°，则∠2的度数为(　A　)A．80°B．70°C．85°D．75°3．(2018·岳阳中考)下列命题是真命题的是(　C　)A．平行四边形的对角线相等B．三角形的重心是三条边的垂直平分线的交点C．五边形的内角和是540°D．圆内接四边形的对角相等4．(2018·攀枝花中考)下列说法正确的是(　D　)A．真命题的逆命题都是真命题B．在同圆或等圆中，同弦或等弦所对的圆周角相等C．等腰三角形的高线、中线、角平分线互相重合D．对角线相等且互相平分的四边形是矩形5．(2018·黄石中考)如图，△ABC中，AD是BC边上的高，AE，BF分别是∠BAC，∠ABC的平分线，∠BAC＝50°，∠ABC＝60°，则∠EAD＋∠ACD＝(　A　)A．75°B．80°C．85°D．90°6．(2018·临沂中考)如图，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别是点D，E，AD＝3，BE＝1，则DE的长是(　B　)A.B．2C．2D.,(第6题图))　　　,(第7题图))　　　,(第8题图))7．(2018·黔西南中考)如图，在▱ABCD中，已知AC＝4cm，若△ACD的周长为13cm，则▱ABCD的周长为(　D　)A．26cmB．24cmC．20cmD．18cm8．(2018·毕节模拟)如图，等边△ABC中，BF是AC边上中线，点D在BF上，连接AD，在AD的右侧作等边△ADE，连接EF，当△AEF周长最小时，∠CFE的大小是(　D　)A．30°B．45°C．60°D．90°9．(2018·龙东中考)如图，平行四边形ABCD的对角线AC，BD相交于点O，AE平分∠BAD，分别交BC，BD于n点E，P，连接OE，∠ADC＝60°，AB＝BC＝1，则下列结论：①∠CAD＝30°；②BD＝；③S平行四边形ABCD＝AB·AC；④OE＝AD；⑤S△APO＝，正确的个数是(　D　)A．2B．3C．4D．5,(第9题图))　　　,(第10题图))10．(2018·潍坊中考)如图，木工师傅在板材边角处作直角时，往往使用“三弧法”，其作法是：(1)作线段AB，分别以A，B为圆心，以AB长为半径作弧，两弧的交点为C；(2)以C为圆心，仍以AB长为半径作弧交AC的延长线于点D；(3)连接BD，BC.下列说法不正确的是(　D　)A．∠CBD＝30°B．S△BDC＝AB2C．点C是△ABD的外心D．sin2A＋cos2D＝1二、填空题(每小题4分，共20分)11．(2018·湘潭中考)《九章算术》是我国古代最重要的数学著作之一，在“勾股”章中记载了一道“折竹抵地”问题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何？”翻译成数学问题是：如图，△ABC中，∠ACB＝90°，AC＋AB＝10，BC＝3，求AC的长．如果设AC＝x，则可列方程为__x2＋32＝(10－x)2__．,(第11题图))　　　,(第12题图))　　　,(第13题图))12．(2018·山西中考)如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B.小宇同学利用尺规按以下步骤作图：①以点A为圆心，以任意长为半径作弧交AN于点C，交AB于点D；②分别以C，D为圆心，以大于CD长为半径作弧，两弧在∠NAB内交于点E；③作射线AE交PQ于点F.若AB＝2，∠ABP＝60°，则线段AF的长为__2__13．(2018·娄底中考)如图，△ABC中，AB＝AC，AD⊥BC于点D，DE⊥AB于点E，BF⊥AC于点F，DE＝3cm，则BF＝__6__cm.14．(2018·云南中考)在△ABC中，AB＝，AC＝5，若BC边上的高等于3，则BC边的长为__9或1__．15．(2018·永州中考)现有A，B两个大型储油罐，它们相距2km，计划修建一条笔直的输油管道，使得A，B两个储油罐到输油管道所在直线的距离都为0.5km，输油管道所在直线符合上述要求的设计方案有__4__种．三、解答题(本大题5小题，共50分)16．(10分)(2018·武汉中考)如图，点E，F在BC上，BE＝CF，AB＝DC，∠B＝∠C，AF与DE交于点G，求证：GE＝GF.n证明：∵BE＝CF，∴BE＋EF＝CF＋EF，∴BF＝CE.在△ABF和△DCE中，∴△ABF≌△DCE(SAS)，∴∠AFB＝∠DEC，即∠GFE＝∠GEF，∴GE＝GF.17．(8分)(2018·岳阳中考)如图，在平行四边形ABCD中，AE＝CF，求证：四边形BFDE是平行四边形．证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD.又∵AE＝CF，∴BE＝DF.又∵BE∥DF，∴四边形BFDE是平行四边形．18．(10分)(2018·安顺中考)如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF.(1)求证：AF＝DC；(2)若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．(1)证明：∵E是AD的中点，∴AE＝ED.∵AF∥BC，∴∠AFE＝∠DBE，∠FAE＝∠BDE.∴△AFE≌△DBE.∴AF＝DB.∵AD是BC边上的中线，∴DB＝DC.n∴AF＝DC；(2)解：四边形ADCF是菱形．证明如下：由(1)知AF＝DC，AF∥CD，∴四边形ADCF是平行四边形．∵AB⊥AC，∴△ABC是直角三角形．∵AD是斜边BC上的中线，∴AD＝BC＝DC.∴平行四边形ADCF是菱形．19.(10分)(2018·绍兴中考)数学课上，张老师举了下面的例题：例1　等腰三角形ABC中，∠A＝110°，求∠B的度数．(答案：35°)例2　等腰三角形ABC中，∠A＝40°，求∠B的度数．(答案：40°或70°或100°)张老师启发同学们进行变式，小敏编了如下一题：变式　等腰三角形ABC中，∠A＝80°，求∠B的度数．(1)请你解答以上的变式题；(2)解(1)后，小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同．如果在等腰三角形ABC中，设∠A＝x°，当∠B有三个不同的度数时，请你探索x的取值范围．解：(1)当∠A为顶角时，∠B＝50°；当∠A为底角时，顶角∠B＝20°，底角∠B＝80°.故∠B＝50°或20°或80°；(2)分两种情况：①当90≤x<180时，∠A只能为顶角，∴∠B的度数只有一个．②当0