2018届八年级数学下册第十七章勾股定理第1课时勾股定理的验证同步练习 6页

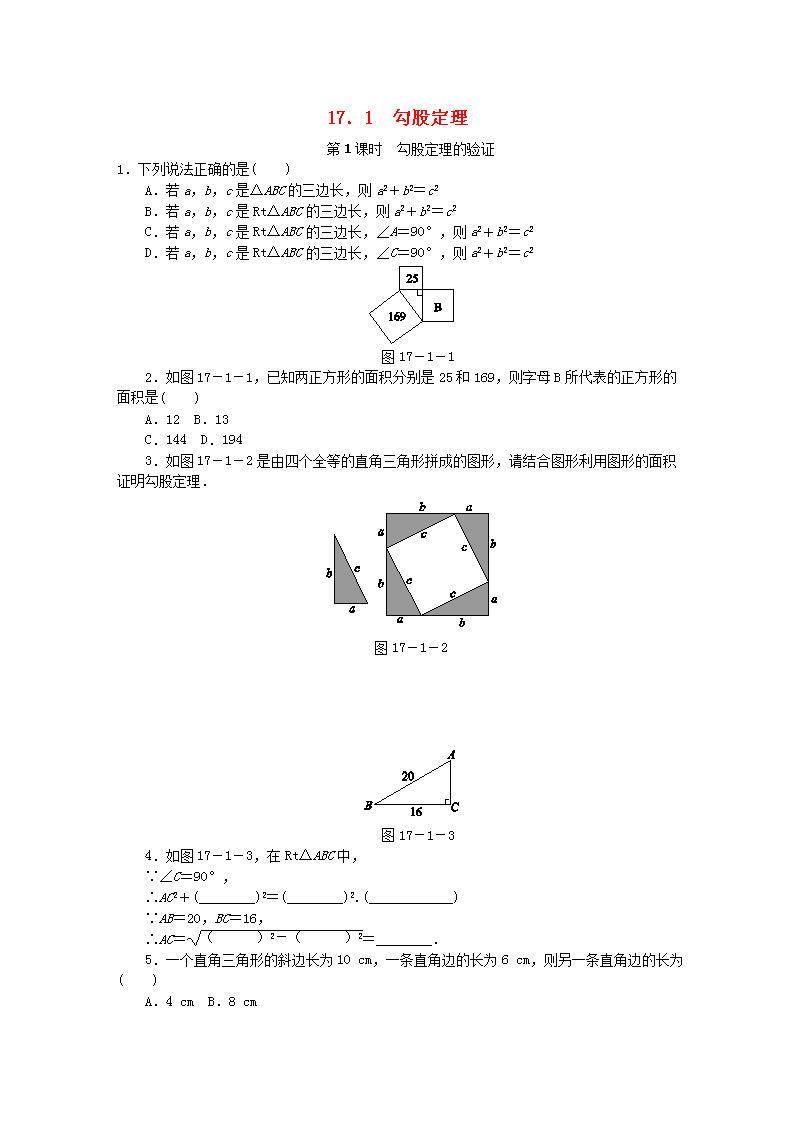
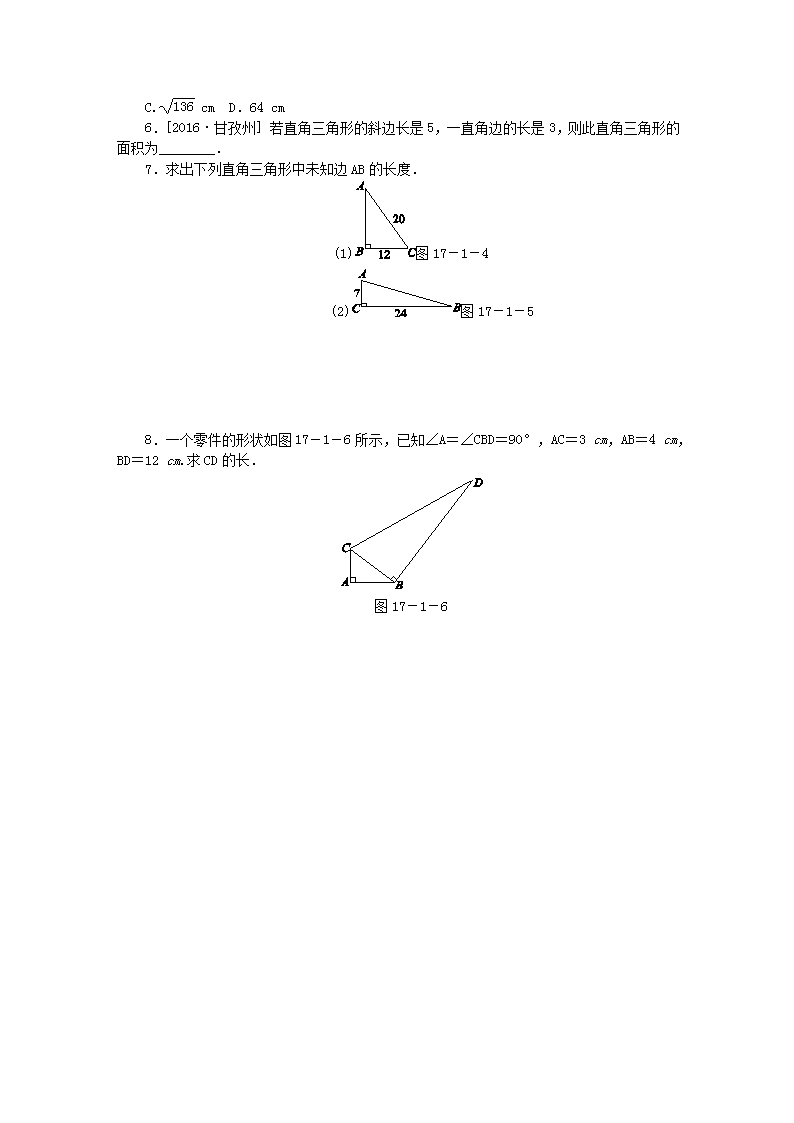
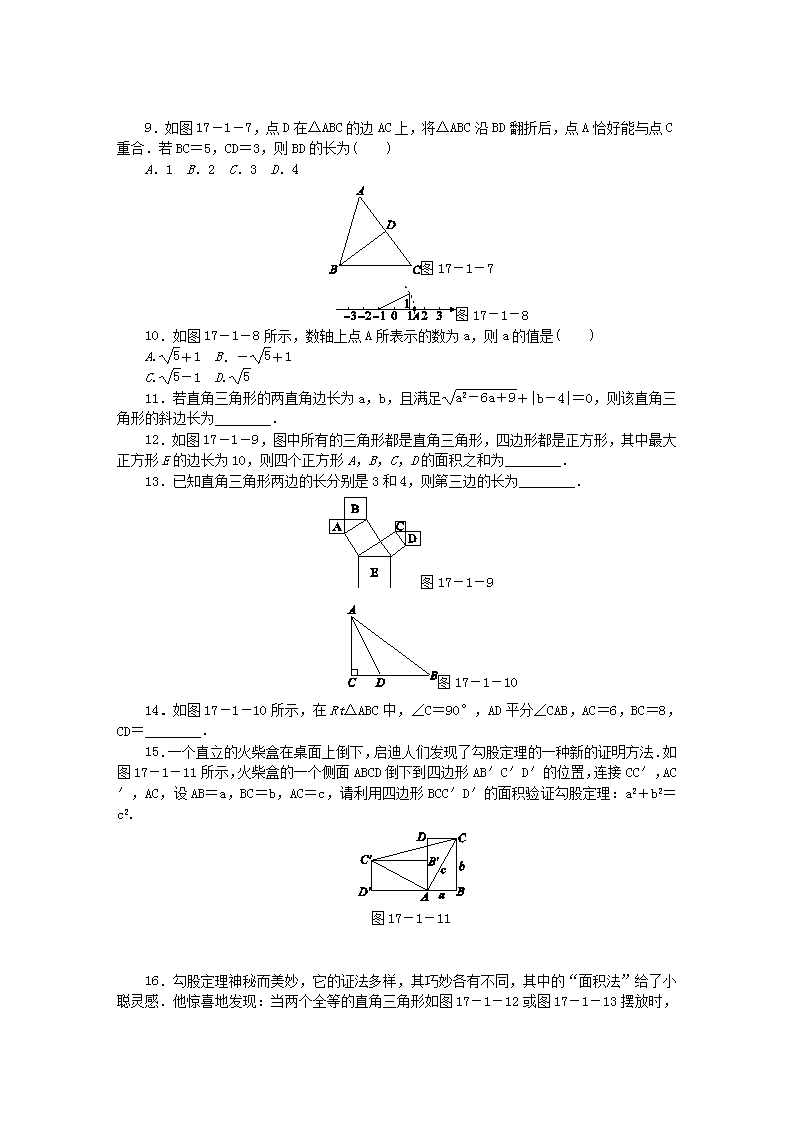
17．1　勾股定理第1课时　勾股定理的验证1．下列说法正确的是(　　)A．若a，b，c是△ABC的三边长，则a2＋b2＝c2B．若a，b，c是Rt△ABC的三边长，则a2＋b2＝c2C．若a，b，c是Rt△ABC的三边长，∠A＝90°，则a2＋b2＝c2D．若a，b，c是Rt△ABC的三边长，∠C＝90°，则a2＋b2＝c2　图17－1－12．如图17－1－1，已知两正方形的面积分别是25和169，则字母B所代表的正方形的面积是(　　)A．12B．13C．144D．1943．如图17－1－2是由四个全等的直角三角形拼成的图形，请结合图形利用图形的面积证明勾股定理．图17－1－2　图17－1－34．如图17－1－3，在Rt△ABC中，∵∠C＝90°，∴AC2＋(________)2＝(________)2.(____________)∵AB＝20，BC＝16，∴AC＝＝________．5．一个直角三角形的斜边长为10cm，一条直角边的长为6cm，则另一条直角边的长为(　　)A．4cmB．8cmnC.cmD．64cm6．[2016·甘孜州]若直角三角形的斜边长是5，一直角边的长是3，则此直角三角形的面积为________．7．求出下列直角三角形中未知边AB的长度．(1)图17－1－4　　　(2)图17－1－58．一个零件的形状如图17－1－6所示，已知∠A＝∠CBD＝90°，AC＝3cm，AB＝4cm，BD＝12cm.求CD的长．图17－1－6n9．如图17－1－7，点D在△ABC的边AC上，将△ABC沿BD翻折后，点A恰好能与点C重合．若BC＝5，CD＝3，则BD的长为(　　)A．1B．2C．3D．4图17－1－7　　　图17－1－810．如图17－1－8所示，数轴上点A所表示的数为a，则a的值是(　　)A.＋1B．－＋1C.－1D.11．若直角三角形的两直角边长为a，b，且满足＋|b－4|＝0，则该直角三角形的斜边长为________．12．如图17－1－9，图中所有的三角形都是直角三角形，四边形都是正方形，其中最大正方形E的边长为10，则四个正方形A，B，C，D的面积之和为________．13．已知直角三角形两边的长分别是3和4，则第三边的长为________．图17－1－9　　　图17－1－1014．如图17－1－10所示，在Rt△ABC中，∠C＝90°，AD平分∠CAB，AC＝6，BC＝8，CD＝________．15．一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法．如图17－1－11所示，火柴盒的一个侧面ABCD倒下到四边形AB′C′D′的位置，连接CC′，AC′，AC，设AB＝a，BC＝b，AC＝c，请利用四边形BCC′D′的面积验证勾股定理：a2＋b2＝c2.图17－1－1116．勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪灵感．他惊喜地发现：当两个全等的直角三角形如图17－1－12或图17－1－13摆放时，n都可以用“面积法”来证明．下面是小聪利用图17－1－12证明勾股定理的过程：将两个全等的直角三角形按图17－1－12所示的方式摆放，其中∠DAB＝90°，求证：a2＋b2＝c2.图17－1－12证明：连接DB，DC，过点D作BC边上的高DF，则DF＝EC＝b－a.∵S四边形ADCB＝S△ACD＋S△ABC＝b2＋ab，S四边形ADCB＝S△ADB＋S△DCB＝c2＋a(b－a)，∴b2＋ab＝c2＋a(b－a)，∴a2＋b2＝c2.请参照上述证法，利用图17－1－13完成下面的证明．将两个全等的直角三角形按图17－1－13所示的方式摆放，其中∠DAB＝90°.求证：a2＋b2＝c2.图17－1－13证明：连接____________________________．∵S五边形ACBED＝________________________，又∵S五边形ACBED＝______________________，∴____________________________________．∴a2＋b2＝c2.n详解详析1．D　[解析]对于选项A，因为只有在直角三角形的前提条件下才能使用勾股定理，所以A项不正确．对于选项B，因为不知道哪一条边是斜边，所以B项不正确．对于选项C，因为∠A＝90°，所以a是斜边长，故应有b2＋c2＝a2，所以C项不正确．只有选项D符合勾股定理的内容．故选D.2．C3．证明：大正方形的面积可表示为(a＋b)2或4×ab＋c2，所以(a＋b)2＝4×ab＋c2，即a2＋2ab＋b2＝2ab＋c2，故a2＋b2＝c2.4．BC　AB　勾股定理　20　16　125．B6．6　[解析]∵直角三角形的斜边长是5，一直角边的长是3，∴另一直角边长为＝4.该直角三角形的面积S＝×3×4＝6.7．解：(1)AB2＝AC2－BC2＝202－122＝400－144＝256，又因为AB>0，所以AB＝16.(2)AB2＝BC2＋AC2＝242＋72＝576＋49＝625，又因为AB>0，所以AB＝25.8．解：在Rt△ABC中，根据勾股定理，得BC2＝AB2＋AC2＝32＋42＝25.在Rt△CBD中，根据勾股定理，得CD2＝BC2＋BD2＝25＋122＝169，所以CD＝13(负值已舍去)．即CD的长为13cm.9．D　[解析]由翻折可得∠BDC＝90°，根据勾股定理可得BD＝＝＝4.10．C　[解析]图中的直角三角形的两直角边长为1和2，∴斜边长为＝，∴表示－1的点到点A的距离是，那么点A所表示的数为－1.11．[5　[解析]∵＋|b－4|＝0，∴a2－6a＋9＝0，b－4＝0，解得a＝3，b＝4.∵直角三角形的两直角边长为a，b，∴该直角三角形的斜边长＝＝5.1210013．5或　[解析]当3，4为两直角边长时，第三边是斜边，其长为5；当长为4的边是斜边时，第三边是直角边，其长为.故第三边长为5或.14．3　[解析]如图，过点D作DE⊥AB于点E.∵∠C＝90°，AC＝6，BC＝8，∴AB＝＝＝10.∵AD平分∠CAB，∴CD＝DE，∴S△ABC＝AC·CD＋AB·DE＝AC·BC，n即×6·CD＋×10·CD＝×6×8，解得CD＝3.15．证明：根据题意得四边形BCC′D′是直角梯形，所以S梯形BCC′D′＝(a＋b)(a＋b)＝a2＋ab＋b2＝ab＋(a2＋b2)．根据题意知△ABC≌△AB′C′，所以∠BAC＝∠B′AC′，所以∠CAC′＝∠DAC＋∠B′AC′＝∠DAC＋∠BAC＝90°，所以S四边形BCC′D′＝S△AD′C′＋S△ABC＋S△AC′C＝ab＋ab＋c2＝ab＋c2，即ab＋(a2＋b2)＝ab＋c2，所以a2＋b2＝c2.16．解：证明：连接DB，过点B作DE边上的高BF，则BF＝b－a.∵S五边形ACBED＝S梯形ACBE＋S△AED＝(a＋b)b＋ab，又∵S五边形ACBED＝S△ACB＋S△ADB＋S△BED＝ab＋c2＋a(b－a)，∴(a＋b)b＋ab＝ab＋c2＋a(b－a)，∴a2＋b2＝c2.