2020版高中数学第二章统计章末复习学案（含解析）新人教b版 14页

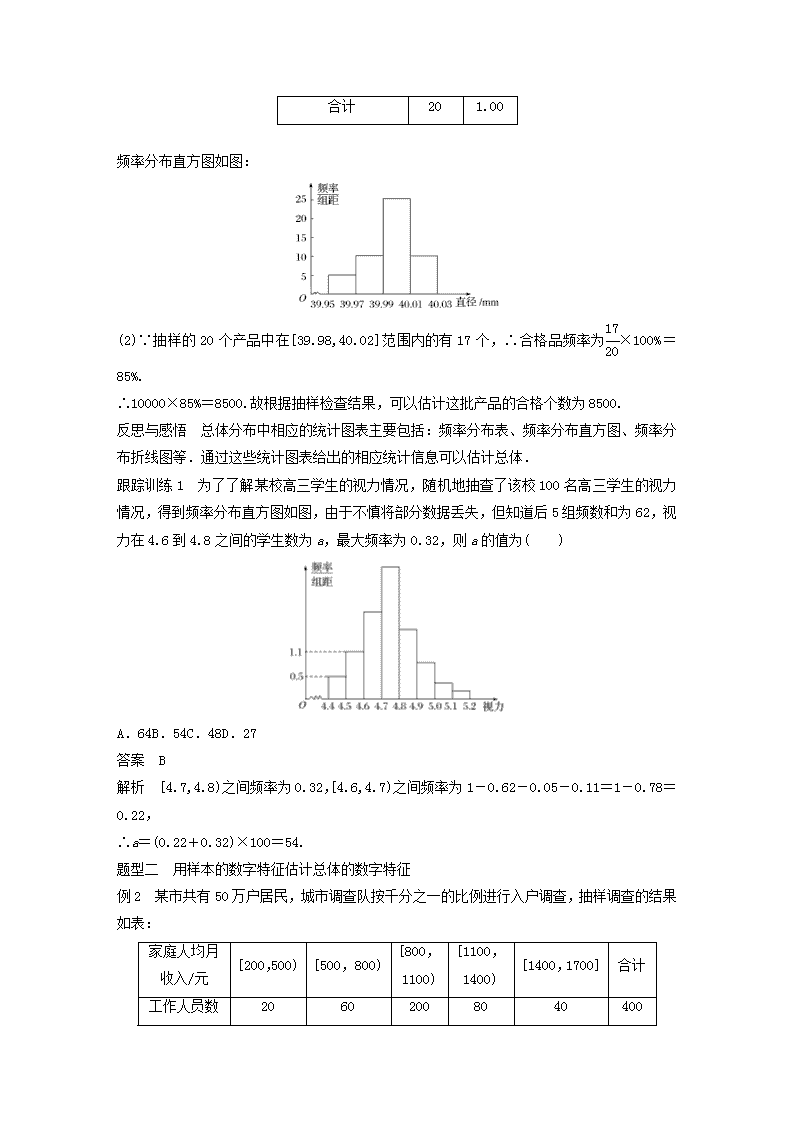
第二章统计章末复习学习目标　1.会根据不同的特点选择适当的抽样方法获得样本数据.2.能利用图、表对样本数据进行整理分析，用样本和样本的数字特征估计总体.3.能利用散点图对两个变量是否相关进行初步判断，能用回归直线方程进行预测．1．抽样方法(1)用随机数表法抽样时，对个体所编号码位数要相同，当问题所给位数不同时，以位数较多的为准，在位数较少的数前面添“0”，凑齐位数．(2)用系统抽样法时，如果总体容量N能被样本容量n整除，抽样间隔为k＝；如果总体容量N不能被样本容量n整除，先用简单随机抽样剔除多余个体，抽样间隔为k＝(其中K＝N－多余个体数)．(3)三种抽样方法的异同点类别共同点各自特点相互联系适用范围简单随机抽样抽样过程中每个个体被抽到的可能性相同从总体中逐个抽取总体中的个体数较少系统抽样将总体平均分成几部分，按事先确定的规则分别在各部分中抽取在起始部分抽样时，采用简单随机抽样总体中的个体数较多分层抽样将总体分成几层，按各层个体数之比抽取在各层抽样时采用简单随机抽样或系统抽样总体由差异明显的几部分组成2.用样本估计总体(1)用样本估计总体用样本频率分布估计总体频率分布时，通常要对给定的一组数据作频率分布表与频率分布直方图．当样本只有两组数据且样本容量比较小时，用茎叶图刻画数据比较方便．(2)样本的数字特征样本的数字特征可分为两大类：一类是反映样本数据集中趋势的，包括众数、中位数和平均数；另一类是反映样本波动大小的，包括方差及标准差．n3．变量间的相关关系(1)两个变量之间的相关关系的研究，通常先作变量的散点图，根据散点图判断这两个变量最接近于哪种确定性关系(函数关系)．(2)求回归直线方程的步骤：①先把数据制成表，从表中计算出，，x，xiyi；②计算回归系数，.公式为③写出回归直线方程＝x＋.题型一　用样本的频率分布估计总体例1　某制造商生产一批直径为40mm的乒乓球，现随机抽样检查20个，测得每个球的直径(单位：mm，保留两位小数)如下：40．03　40.00　39.98　40.00　39.99　40.00　39.9840．01　39.98　39.99　40.00　39.99　39.95　40.0140．02　39.98　40.00　39.99　40.00　39.96(1)完成下面的频率分布表，并画出频率分布直方图；分组频数频率[39.95,39.97)[39.97,39.99)[39.99,40.01)[40.01,40.03]合计(2)假定乒乓球的直径误差不超过0.02mm为合格品．若这批乒乓球的总数为10000，试根据抽样检查结果估计这批产品的合格个数．解　(1)频率分布表如下：分组频数频率[39.95,39.97)20.10[39.97,39.99)40.20[39.99,40.01)100.50[40.01,40.03]40.20n合计201.00频率分布直方图如图：(2)∵抽样的20个产品中在[39.98,40.02]范围内的有17个，∴合格品频率为×100%＝85%.∴10000×85%＝8500.故根据抽样检查结果，可以估计这批产品的合格个数为8500.反思与感悟　总体分布中相应的统计图表主要包括：频率分布表、频率分布直方图、频率分布折线图等．通过这些统计图表给出的相应统计信息可以估计总体．跟踪训练1　为了了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图如图，由于不慎将部分数据丢失，但知道后5组频数和为62，视力在4.6到4.8之间的学生数为a，最大频率为0.32，则a的值为(　　)A．64B．54C．48D．27答案　B解析　[4.7,4.8)之间频率为0.32，[4.6,4.7)之间频率为1－0.62－0.05－0.11＝1－0.78＝0.22，∴a＝(0.22＋0.32)×100＝54.题型二　用样本的数字特征估计总体的数字特征例2　某市共有50万户居民，城市调查队按千分之一的比例进行入户调查，抽样调查的结果如表：家庭人均月收入/元[200，500)[500，800)[800，1100)[1100，1400)[1400，1700]合计工作人员数20602008040400n管理人员数510502015100求：(1)工作人员家庭人均月收入的估计值1及方差的估计值s；(2)管理人员家庭人均月收入的估计值2及方差的估计值s；(3)总体人均月收入的估计值及总体方差的估计值s2.解　(1)1＝×(20×350＋60×650＋200×950＋80×1250＋40×1550)＝995，s＝×[20×(350－995)2＋60×(650－995)2＋200×(950－995)2＋80×(1250－995)2＋40×(1550－995)2]＝83475.(2)2＝×(5×350＋10×650＋50×950＋20×1250＋15×1550)＝1040，s＝×[5×(350－1040)2＋10×(650－1040)2＋50×(950－1040)2＋20×(1250－1040)2＋15×(1550－1040)2]＝90900.(3)＝×(25×350＋70×650＋250×950＋100×1250＋55×1550)＝1004，s2＝×[25×(350－1004)2＋70×(650－1004)2＋250×(950－1004)2＋100×(1250－1004)2＋55×(1550－1004)2]＝85284.反思与感悟　样本的数字特征分为两大类：一类是反映样本数据集中趋势的特征数，例如平均数；另一类是反映样本数据波动大小的特征数，例如方差和标准差．通常我们用样本的平均数和方差(标准差)来近似代替总体的平均数和方差(标准差)，从而实现对总体的估计．跟踪训练2　对甲、乙的学习成绩进行抽样分析，各抽5门功课，得到的观测数据如下：甲6080709070乙8060708075问：甲、乙谁的平均成绩好？谁的各门功课发展较平衡？解　甲的平均成绩为甲＝74，乙的平均成绩为乙＝73.所以甲的平均成绩好．甲的方差是s＝[(－14)2＋62＋(－4)2＋162＋(－4)2]＝104，乙的方差是s＝×[72＋(－13)2＋(－3)2＋72＋22]＝56.因为s>s，所以乙的各门功课发展较平衡．题型三　用回归直线方程对总体进行估计例3　某车间为了制定工时定额，需要确定加工零件所花费的时间，为此做了四次试验，得到的数据如下：n零件的个数x(个)2345加工的时间y(小时)2.5344.5(注：＝，＝－)(1)在给定的坐标系中画出表中数据的散点图；(2)求出y关于x的回归直线方程＝x＋，并在坐标系中画出回归直线；(3)试预测加工10个零件需要多少小时？解　(1)散点图如图．(2)由表中数据得：iyi＝52.5，＝3.5，＝3.5，＝54，∴＝0.7，∴＝1.05，∴＝0.7x＋1.05，回归直线如图所示．(3)将x＝10代入回归直线方程，n得＝0.7×10＋1.05＝8.05，故预测加工10个零件约需要8.05小时．反思与感悟　对两个变量进行研究，通常是先作出两个变量之间的散点图，根据散点图直观判断两个变量是否具有线性相关关系，如果具有，就可以应用最小二乘法求回归直线方程．由于样本可以反映总体，所以可以利用所求的回归直线方程，对这两个变量所确定的总体进行估计，即根据一个变量的取值，预测另一个变量的取值．跟踪训练3　理论预测某城市2020到2024年人口总数与年份的关系如下表所示：年份202x(年)01234人口数y(十万)5781119(1)请画出上表数据的散点图；(2)指出x与y是否线性相关；(3)若x与y线性相关，请根据上表提供的数据，用最小二乘法求出y关于x的回归直线方程＝x＋；(4)据此估计2025年该城市人口总数．(参数数据：0×5＋1×7＋2×8＋3×11＋4×19＝132,02＋12＋22＋32＋42＝30)解　(1)数据的散点图如图：(2)由散点图可知，样本点基本上分布在一条直线附近，故x与y呈线性相关．(3)由表知＝×(0＋1＋2＋3＋4)＝2，＝×(5＋7＋8＋11＋19)＝10.∴＝＝3.2，＝－＝3.6，∴回归直线方程为＝3.2x＋3.6.(4)当x＝5时，＝19.6(十万)＝196万．n故2025年该城市人口总数约为196万．1．10个小球分别编有号码1,2,3,4，其中1号球4个，2号球2个，3号球3个，4号球1个，则数0.4是指1号球占总体分布的(　　)A．频数B．频率C．D．以上都不对答案　B2．现有10个数，其平均数是4，且这10个数的平方和是200，那么这组数的标准差是(　　)A．1B．2C．3D．4答案　B解析　设这10个数为a1，a2，…，a10，则有a＋a＋…＋a＝200，且a1＋a2＋…＋a10＝40，所以＝＝＝4，∴标准差为＝2.3．某班50名学生的一次数学质量测验成绩的频率分布直方图如图所示，则成绩不低于70分的学生人数是____________________________________________________．答案　35解析　低于70分的频率为(0.012＋0.018)×10＝0.3，所以不低于70分的频率为0.7，故不低于70分的人数为50×0.7＝35.n4．某农田施肥量x(单位：kg)与小麦产量y(单位：kg)之间的回归直线方程是＝4x＋250，则当施肥量为50kg时，可以预测小麦的产量为________kg.答案　450解析　直接将x＝50代入回归直线方程中，可得＝4×50＋250＝450.5．从某学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组；第一组[155,160)，第二组[160,165)，…，第八组[190,195]．如图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组的人数相同，第六组的人数为4.(1)求第七组的频率；(2)估计该校的800名男生的身高的中位数以及身高在180cm以上(含180cm)的人数．解　(1)第六组的频率为＝0.08，所以第七组的频率为1－0.08－5×(0.008×2＋0.016＋0.04×2＋0.06)＝0.06.(2)身高在第一组[155,160)的频率为0.008×5＝0.04，身高在第二组[160,165)的频率为0.016×5＝0.08，身高在第三组[165,170)的频率为0.04×5＝0.2，身高在第四组[170,175)的频率为0.04×5＝0.2，由于0.04＋0.08＋0.2＝0.32＜0.5,0.04＋0.08＋0.2＋0.2＝0.52＞0.5，估计这所学校的800名男生的身高的中位数为m，则170＜m＜175，由0.04＋0.08＋0.2＋(m－170)×0.04＝0.5，得m＝174.5，所以可估计这所学校的800名男生的身高的中位数为174.5，由直方图得后三组频率之和为0.06＋0.08＋0.008×5＝0.18，所以身高在180cm以上(含180cm)的人数为0.18×800＝144.n1.用频率分布直方图解决相关问题时，应正确理解图中各个量的意义，识图掌握信息是解决该类问题的关键.频率分布直方图有以下几个特点：(1)纵轴表示频率/组距；(2)频率分布直方图中各小长方形高的比就是相应各组的频率之比；(3)直方图中各小长方形的面积是相应各组的频率，所有的小长方形的面积之和等于1，即频率之和为1.2.平均数、中位数、众数与方差、标准差都是重要的数字特征，利用它们可对总体进行一种简明的描述，它们所反映的情况有着重要的实际意义，平均数、中位数、众数可描述总体的集中趋势，方差和标准差可描述波动大小.一、选择题1．在某次商品促销活动中，某人可得到4件不同的奖品，这些奖品要从40件不同的奖品中随机抽取决定．用系统抽样的方法确定这个人所得到的4件奖品的编号，有可能的是(　　)A．3,9,15,11B．3,12,21,40C．8,20,32,40D．2,12,22,32答案　D解析　由系统抽样的方法可知，这个人所得到的4件奖品的编号的间隔相等，且平均分布在1～10,11～20,21～30,31～40中，故A，B，C均不正确，D正确．2．某中学有高中生3500人，初中生1500人，为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为n的样本，已知从高中生中抽取70人，则n等于(　　)A．100B．150C．200D．250答案　A解析　∵＝，∴n＝100.3．为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分(十分制)如图所示，假设得分值的中位数为me，众数为mo，平均值为，则(　　)A．me＝mo＝B．me＝mo＜C．me＜mo＜D．mo＜me＜答案　Dn解析　30个数中第15个数是5，第16个数是6，所以中位数me＝＝5.5，众数mo＝5，平均值＝＝，∴mo