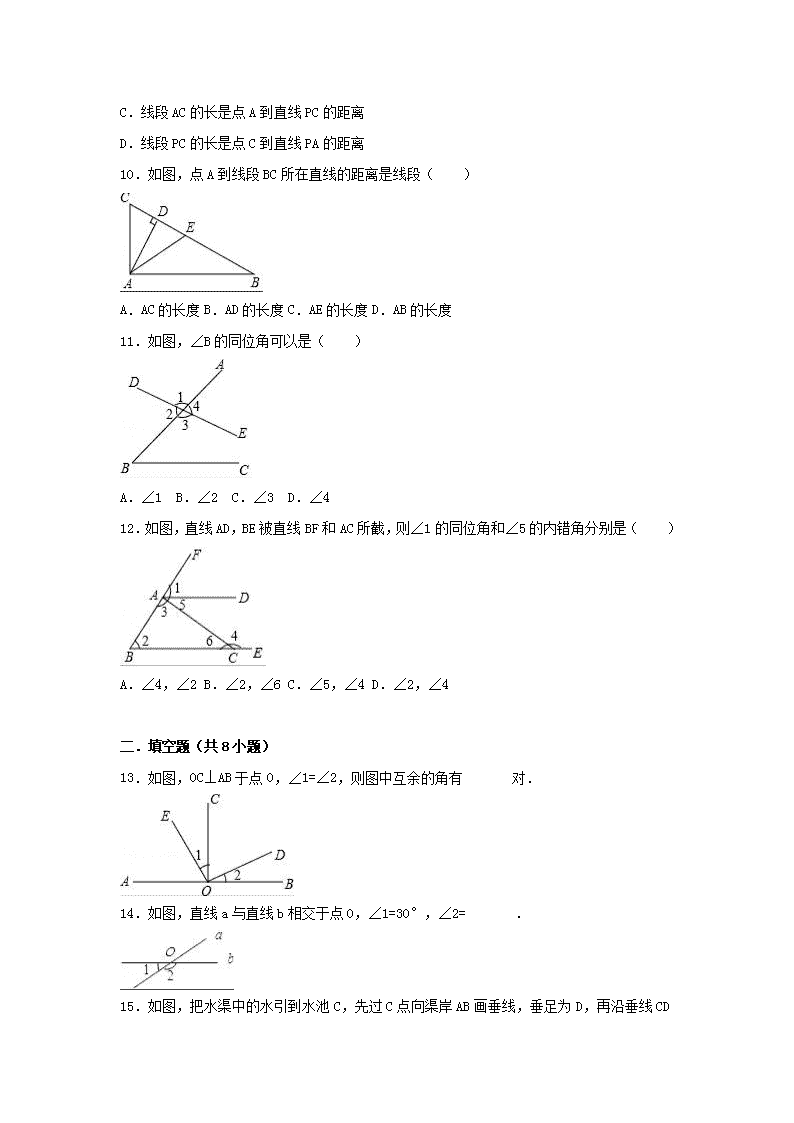- 112.59 KB
- 2022-04-12 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
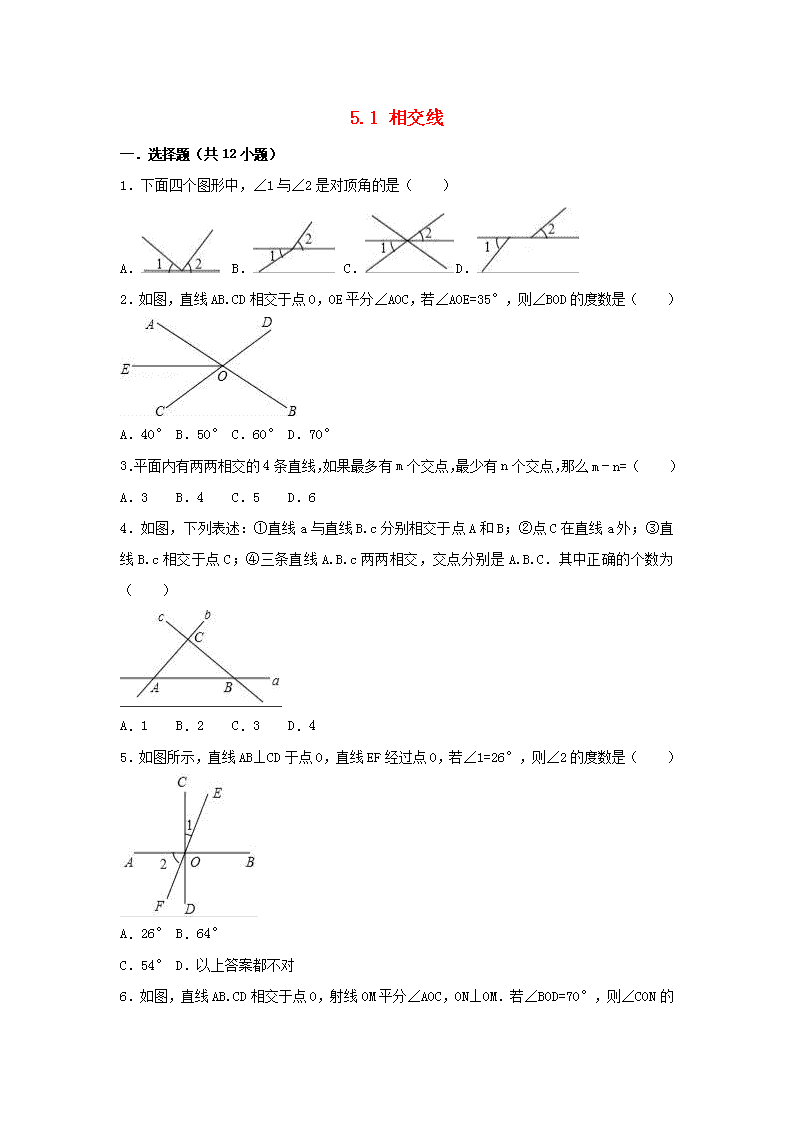
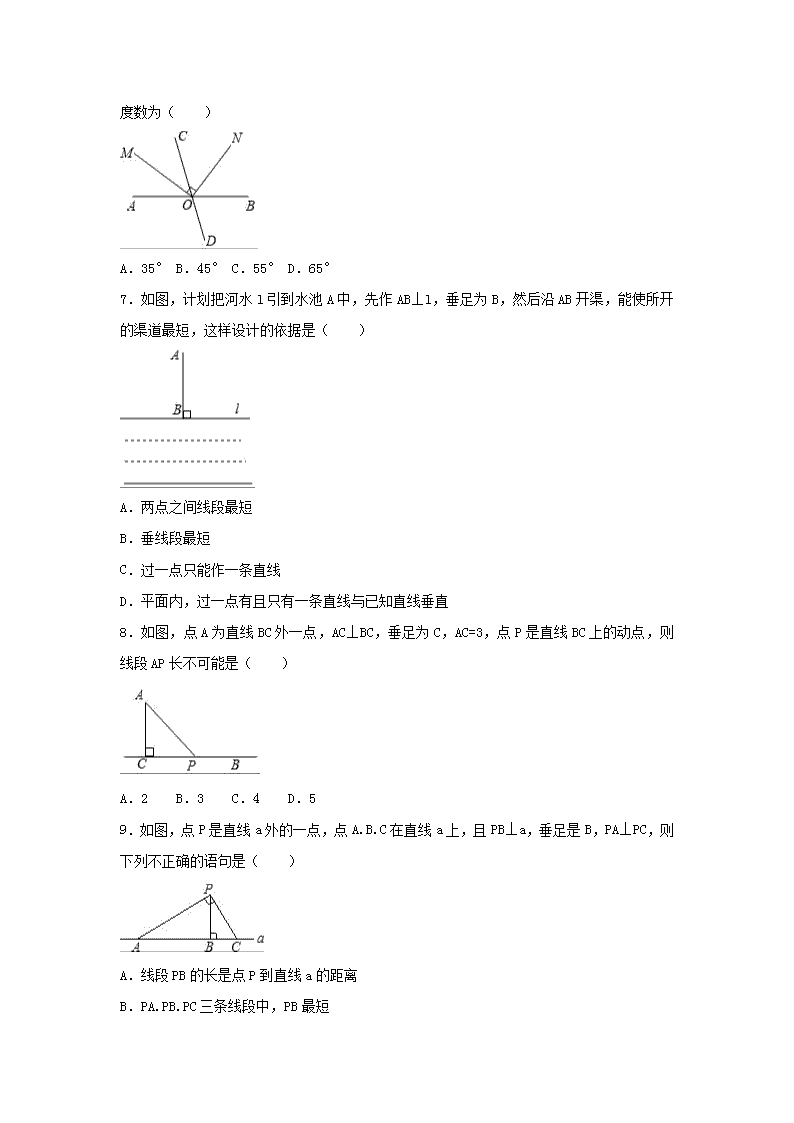
5.1相交线一.选择题(共12小题)1.下面四个图形中,∠1与∠2是对顶角的是( )A.B.C.D.2.如图,直线AB.CD相交于点O,OE平分∠AOC,若∠AOE=35°,则∠BOD的度数是( )A.40°B.50°C.60°D.70°3.平面内有两两相交的4条直线,如果最多有m个交点,最少有n个交点,那么m﹣n=( )A.3B.4C.5D.64.如图,下列表述:①直线a与直线B.c分别相交于点A和B;②点C在直线a外;③直线B.c相交于点C;④三条直线A.B.c两两相交,交点分别是A.B.C.其中正确的个数为( )A.1B.2C.3D.45.如图所示,直线AB⊥CD于点O,直线EF经过点O,若∠1=26°,则∠2的度数是( )A.26°B.64°C.54°D.以上答案都不对6.如图,直线AB.CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠BOD=70°,则∠nCON的度数为( )A.35°B.45°C.55°D.65°7.如图,计划把河水l引到水池A中,先作AB⊥l,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是( )A.两点之间线段最短B.垂线段最短C.过一点只能作一条直线D.平面内,过一点有且只有一条直线与已知直线垂直8.如图,点A为直线BC外一点,AC⊥BC,垂足为C,AC=3,点P是直线BC上的动点,则线段AP长不可能是( )A.2B.3C.4D.59.如图,点P是直线a外的一点,点A.B.C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是( )A.线段PB的长是点P到直线a的距离B.PA.PB.PC三条线段中,PB最短nC.线段AC的长是点A到直线PC的距离D.线段PC的长是点C到直线PA的距离10.如图,点A到线段BC所在直线的距离是线段( )A.AC的长度B.AD的长度C.AE的长度D.AB的长度11.如图,∠B的同位角可以是( )A.∠1B.∠2C.∠3D.∠412.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )A.∠4,∠2B.∠2,∠6C.∠5,∠4D.∠2,∠4 二.填空题(共8小题)13.如图,OC⊥AB于点O,∠1=∠2,则图中互余的角有 对.14.如图,直线a与直线b相交于点O,∠1=30°,∠2= .n15.如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为D,再沿垂线CD开沟才能使沟最短,其依据是 .16.如图,BC⊥AC,BC=8,AC=6,AB=10,则点C到线段AB的距离是 .17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC:∠COE=3:2,则∠AOD= .18.直线AB.CD.EF交于点O,则∠1+∠2+∠3= 度.19.如图,BO⊥AO,∠BOC与∠BOA的度数之比为1:5,那么∠COA= ,∠BOC的补角= .20.如图,当剪子口∠AOB增大15°时,∠COD增大 度.n 三.解答题(共3小题)21.如图,已知直线BC.DE交于O点,OA.OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°.求∠AOD的度数.22.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=80°,求∠BOD的度数;(2)若∠EOC=∠EOD,求∠BOD的度数.n23.如图,直线AB,CD相交于O点,OM平分∠AOB.(1)若∠1=∠2,求∠NOD的度数;(2)若∠BOC=4∠1,求∠AOC与∠MOD的度数. n参考答案一.选择题(共12小题)1.解:由对顶角的定义,得C是对顶角,故选:C. 2.解:∵直线AB.CD相交于点O,OE平分∠AOC,∠AOE=35°,∴∠EOC=∠AOE=35°,∴∠AOC=∠BOD=70°.故选:D. 3.解:如图所示:4条直线两两相交,有3种情况:4条直线经过同一点,有一个交点;3条直线经过同一点,被第4条直线所截,有4个交点;4条直线不经过同一点,有6个交点.故平面内两两相交的4条直线,最多有6个交点,最少有1个交点;即m=6,n=1,则m﹣n=5.故选:C. 4.解:由题意,得①直线a与直线B.c分别相交于点A和B;②点C在直线a外;③直线B.c相交于点C;④三条直线A.B.c两两相交,交点分别是A.B.C,n故选:D. 5.解:∵∠1=26°,∠DOF与∠1是对顶角,∴∠DOF=∠1=26°,又∵∠DOF与∠2互余,∴∠2=90°﹣∠DOF=90°﹣26°=64°.故选:B. 6.解:∵∠BOD=∠AOC=70°,射线OM平分∠AOC,∴∠AOM=∠MOC=35°,∵ON⊥OM,∴∠COM=90°﹣35°=55°.故选:C. 7.解:计划把河水l引到水池A中,先作AB⊥l,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是垂线段最短,故选:B. 8.解:∵AC⊥BC,∴AP≥AC,即AP≥3.故选:A. 9.n解:A.根据点到直线的距离的定义:即点到这一直线的垂线段的长度.故此选项正确;B.根据垂线段最短可知此选项正确;C.线段AP的长是点A到直线PC的距离,故选项错误;D.根据点到直线的距离即点到这一直线的垂线段的长度.故此选项正确.故选:C. 10.解:点A到线段BC所在直线的距离是线段AD的长度,故选:B. 11.解:∠B的同位角可以是:∠4.故选:D. 12.解:∠1的同位角是∠2,∠5的内错角是∠6,故选:B. 二.填空题(共8小题)13.解:∵OC⊥AB,∴∠1+∠AOE=90°,∠2+∠COD=90°,即∠1与∠AOE互为余角,∠2与∠COD互为余角,又∵∠1=∠2,则相互交换又多了两对互余角.即∠1与∠COD互为余角,∠2与∠AOE互为余角.所以共有4对.故答案为:4. 14.n解:∵∠1+∠2=180°,又∠1=30°,∴∠2=150°. 15.解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.故答案为:垂线段最短. 16.解:设点C到线段AB的距离是x,∵BC⊥AC,∴S△ABC=AB•x=AC•BC,即×10•x=×6×8,解得x=4.8,即点C到线段AB的距离是4.8.故答案为:4.8. 17.解:∵EO⊥AB,∴∠AOE=90°,∵∠AOC:∠COE=3:2,∴设∠AOC=3x,∠COE=2x,则3x+2x=90°,解得:x=18°,故∠AOC=54°,则∠AOD=180°﹣54°=126°.故答案为:126°. 18.n解:如图,∠BOD=∠1,∵∠2+∠3+∠BOD=180°,∴∠1+∠2+∠3=180°.故答案为:180 19.解:∵BO⊥AO,∠BOC与∠BOA的度数之比为1:5,∴∠COA=×90°=72°,则∠BOC=18°,故∠BOC的补角=180°﹣18°=162°.故答案为:72°,162°. 20.解:因为∠AOB与∠COD是对顶角,∠AOB与∠COD始终相等,所以随∠AOB变化,∠COD也发生同样变化.故当剪子口∠AOB增大15°时,∠COD也增大15°. 三.解答题(共3小题)21.解:∵OF平分∠COE,∴∠EOF=∠FOC=17°,∴∠EOC=34°,∴∠BOD=34°,∵OA⊥BC,∴∠AOB=90°,∴∠AOD=∠AOB+∠BOD=90°+34°=124°. 22.解:(1)∵OA平分∠EOC,n∴∠AOC=∠EOC=×80°=40°,∴∠BOD=∠AOC=40°;(2)设∠EOC=x,∠EOD=x,根据题意得x+x=180°,解得x=90°,∴∠EOC=x=90°,∴∠AOC=∠EOC=×90°=45°,∴∠BOD=∠AOC=45°. 23.解:(1)∵OM平分∠AOB,∴∠1+∠AOC=90°,∵∠1=∠2,∴∠2+∠AOC=90°,∴∠NOD=180°﹣90°=90°;(2)∵∠BOC=4∠1,∴90°+∠1=4∠1,∴∠1=30°,∴∠AOC=90°﹣30°=60°,∠MON=180°﹣30°=150°.