七年级数学下册第9章多边形9.1三角形9.1.1认识三角形同步练习（新版）华东师大版 4页

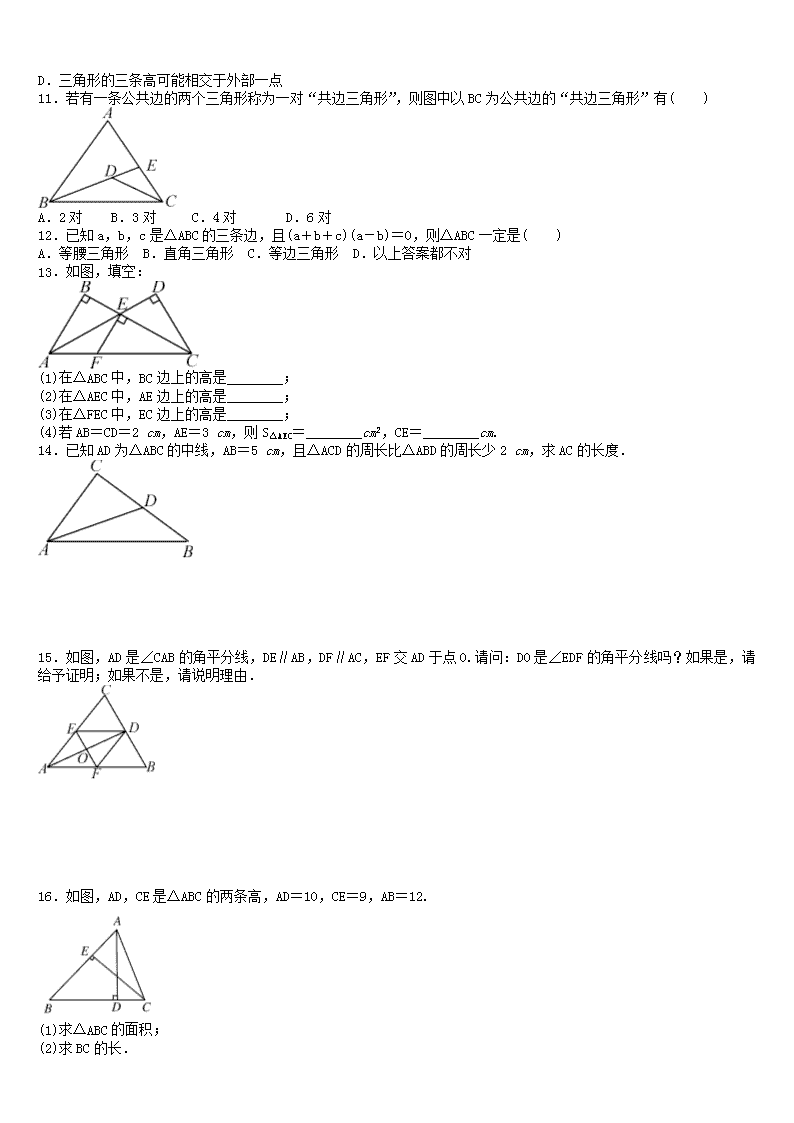
9．1.1　认识三角形1．如图所示，图中共有____个三角形，其中以BC为一边的三角形是_________________；以∠A为一个内角的三角形是______________．2．如图，△ABC有________个内角，________个外角，与∠ABC相邻的外角有________个，它们的关系是________，∠ABC的一个外角与∠ABC的关系是________；当AB＝AC＝BC时，△ABC是________三角形，也称________三角形．3．下列说法正确的有(　　)①等腰三角形是等边三角形；②三角形按边分类可分为等腰三角形、等边三角形和不等边三角形；③三角形的外角与和它相邻的内角互补；④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形．A．①②B．①③④C．③④D．①②④4．下列说法正确的是(　　)A．所有的等腰三角形都是锐角三角形B．等边三角形属于等腰三角形C．不存在既是钝角三角形又是等腰三角形的三角形D．一个三角形里有两个锐角，则一定是锐角三角形5．如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是(　　)6．三角形一边上的中线把原三角形一定分成两个(　　)A．形状相同的三角形B．面积相等的三角形C．直角三角形D．周长相等的三角形7．如图所示，AD是△ABC的角平角线，AE是△ABD的角平分线，若∠BAC＝80°，则∠EAD的度数是(　　)A．20°B．30°C．45°D．60°8．如图所示，D是BC的中点，E是AC的中点，若S△ADE＝1，则S△ABC＝________.9．如图，在△ABC中，∠BAC＝60°，∠ACE＝40°，AD，CE是△ABC的角平分线，则∠DAC＝________，∠BCE＝________，∠ACB＝________.10．下列说法错误的是(　　)A．三角形的三条高一定在三角形内部交于一点B．三角形的三条中线一定在三角形内部交于一点C．三角形的三条角平分线一定在三角形内部交于一点nD．三角形的三条高可能相交于外部一点11．若有一条公共边的两个三角形称为一对“共边三角形”，则图中以BC为公共边的“共边三角形”有(　　)A．2对B．3对C．4对D．6对12．已知a，b，c是△ABC的三条边，且(a＋b＋c)(a－b)＝0，则△ABC一定是(　　)A．等腰三角形B．直角三角形C．等边三角形D．以上答案都不对13．如图，填空：(1)在△ABC中，BC边上的高是________；(2)在△AEC中，AE边上的高是________；(3)在△FEC中，EC边上的高是________；(4)若AB＝CD＝2cm，AE＝3cm，则S△AEC＝________cm2，CE＝________cm.14．已知AD为△ABC的中线，AB＝5cm，且△ACD的周长比△ABD的周长少2cm，求AC的长度．15．如图，AD是∠CAB的角平分线，DE∥AB，DF∥AC，EF交AD于点O.请问：DO是∠EDF的角平分线吗？如果是，请给予证明；如果不是，请说明理由．16．如图，AD，CE是△ABC的两条高，AD＝10，CE＝9，AB＝12.(1)求△ABC的面积；(2)求BC的长．n17．如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC＝4cm2，求阴影部分的面积S阴影。答案：1.5△ABC，△DBC，△ECB，△ABC△EAB2.三六两相等互补等边正3.C4.B5.A6.B7.A8.49.30°40°80°10.A11.B12.A13.(1)AB(2)CD(3)FE(4)3314.∴AD为△ABC的中线，∴BD＝CD，∵△ACD的周长比△ABD的周长少2cm，∴(AB＋BD＋AD)－(AC＋AD＋CD)＝AB－AC＝2cm∴AC＝AB－2＝5－2＝3(cm)15.DO是∠EDF的角平分线，证明：∵AD是∠CAB的角平分线，∴∠EAD＝∠FAD，∵DE∥AB，DF∥AC，∴∠EDA＝∠FAD，∠FDA＝∠EAD，∴∠EDA＝∠FDA，∴DO是∠EDF的角平分线16.(1)S△ABC＝AB×CE＝×12×9＝54　(2)由S△ABC＝BC×AD＝54，n得×BC×10＝54，所以BC＝10.817.∵D是边BC的中点，∴S△ABD＝S△ACD＝S△ABC＝×4＝2cm2.∵E是AD的中点．∴S△BDE＝S△ABD＝1cm2.S△CDE＝S△ACD＝1cm2，S△BEC＝S△BDE＋S△CDE＝2cm2.又∵F是CE的中点，∴S阴影＝S△BEC＝1cm2