- 73.23 KB
- 2022-04-12 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
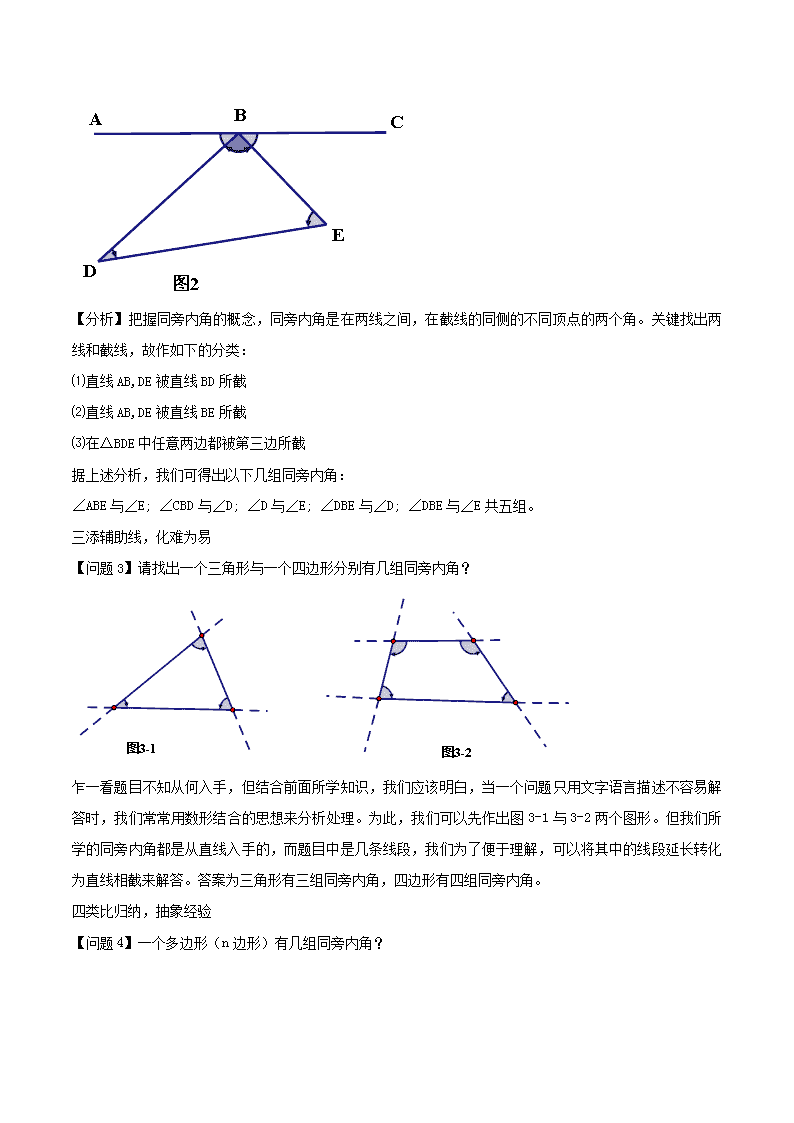
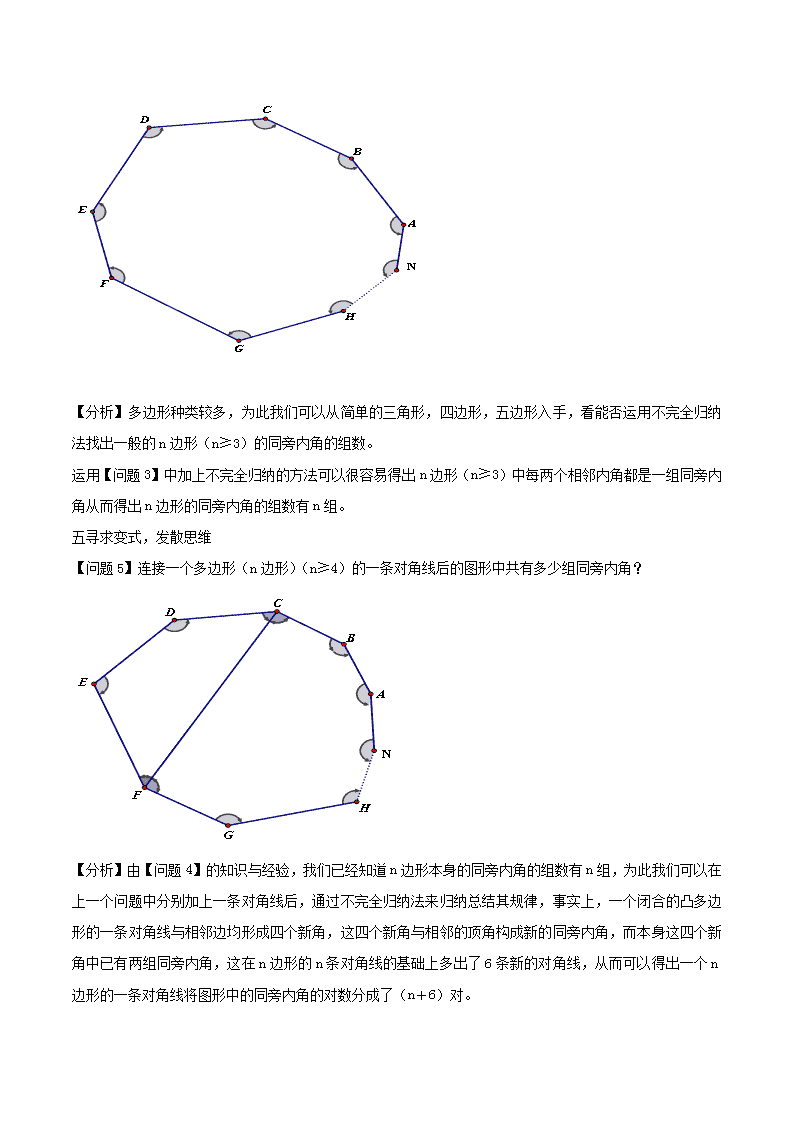
在寻找同旁内角中培养学生的发散思维摘要:七年级学生刚进入中学阶段对几何的学习还大都停留于具体形象阶段,教师在进行该阶段几何教学时要注意培养学生一些处理几何问题的方法,在这里我主要研究了一下在寻找同旁内角中培养学生的发散思维。在进行同旁内角这一节的教学时,我们首先要让同学学会寻找同旁内角,并在探索过程中培养学生的发散思维。关键词:同旁内角;数形结合;发散思维;不完全归纳法众所周知,寻找同旁内角是人教版七年级下数学科目的一个教学难点,鄙人认为在进行该知识教学时可以从概念入手,引导学生从一些规则的几何体中来发现并通过不完全归纳法来总结一些特殊图形的同旁内角的找法。尤其是总结一些特殊图形的同旁内角的组数与某些特定角的同旁内角的个数问题,我们可以从以下几点出发。一强化概念,明确特征【问题1】如图1,直线AB直线CD被直线EF所截,∠1与∠2;∠3与∠4分别有什么共同特点?特点有:⑴分别有两个顶点⑵分别在两直线之间⑶分别在第三条直线的同侧我们把同时满足以上三个条件形成一个“U”字形的图形中的两个角叫做同旁内角。二巧妙变化,丰富外延【问题2】如图2,请找出图2中共有几组同旁内角?n【分析】把握同旁内角的概念,同旁内角是在两线之间,在截线的同侧的不同顶点的两个角。关键找出两线和截线,故作如下的分类:⑴直线AB,DE被直线BD所截⑵直线AB,DE被直线BE所截⑶在△BDE中任意两边都被第三边所截据上述分析,我们可得出以下几组同旁内角:∠ABE与∠E;∠CBD与∠D;∠D与∠E;∠DBE与∠D;∠DBE与∠E共五组。三添辅助线,化难为易【问题3】请找出一个三角形与一个四边形分别有几组同旁内角?乍一看题目不知从何入手,但结合前面所学知识,我们应该明白,当一个问题只用文字语言描述不容易解答时,我们常常用数形结合的思想来分析处理。为此,我们可以先作出图3-1与3-2两个图形。但我们所学的同旁内角都是从直线入手的,而题目中是几条线段,我们为了便于理解,可以将其中的线段延长转化为直线相截来解答。答案为三角形有三组同旁内角,四边形有四组同旁内角。四类比归纳,抽象经验【问题4】一个多边形(n边形)有几组同旁内角?n【分析】多边形种类较多,为此我们可以从简单的三角形,四边形,五边形入手,看能否运用不完全归纳法找出一般的n边形(n≥3)的同旁内角的组数。运用【问题3】中加上不完全归纳的方法可以很容易得出n边形(n≥3)中每两个相邻内角都是一组同旁内角从而得出n边形的同旁内角的组数有n组。五寻求变式,发散思维【问题5】连接一个多边形(n边形)(n≥4)的一条对角线后的图形中共有多少组同旁内角?【分析】由【问题4】的知识与经验,我们已经知道n边形本身的同旁内角的组数有n组,为此我们可以在上一个问题中分别加上一条对角线后,通过不完全归纳法来归纳总结其规律,事实上,一个闭合的凸多边形的一条对角线与相邻边均形成四个新角,这四个新角与相邻的顶角构成新的同旁内角,而本身这四个新角中已有两组同旁内角,这在n边形的n条对角线的基础上多出了6条新的对角线,从而可以得出一个n边形的一条对角线将图形中的同旁内角的对数分成了(n+6)对。n【问题6】一个n边形从同一个顶点出发引2条,3条,…,m(m≤n(n-3)÷2)条对角线后图形中共有多少组同旁内角?【分析】由【问题5】的方法知,需要用数形结合的思想,从简单到复杂的认知规律来不完全归纳出其结果,其中要考虑m条对角线是否有无相邻顶点的连线。再看可以组成多少个简单的多边形图形。然后考虑每个多边形相加共有多少组同旁内角,再减去数重了的同旁内角就是我们要求得得结果。六举一反三,创新思维【问题7】n边形内一点连接到各顶点的图形又有几组同旁内角呢?n边形外一点情形又如何?(本问题比较复杂,这里不讨论n边形内或者外的一点与各顶点共线的情形。)【注】点I与点K分别是n边形ABCDEFGH…N内与外的一点。【分析】n边形内一点连接到各顶点的图形将n边形分成n个三角形,n个四边形,n个五边形,…,1个n边形,我们可以先计算出这些图形中的同旁内角的总个数,再减去数重了的同旁内角的个数就可以得出最n终的结果。总之,在处理同旁内角这个知识点时要把握住同旁内角的内含的主要属性,必要时可以延长相关线段或射线来简化问题,再就结合数形结合的思维方式,辅助以不完全归纳法,从而可以让学生依据从简单到复杂认知规律不断发展学生的数学思维。