九年级数学下册第二十七章圆27.1圆的认识圆周角与圆心角、弧的关系学案华东师大版 5页

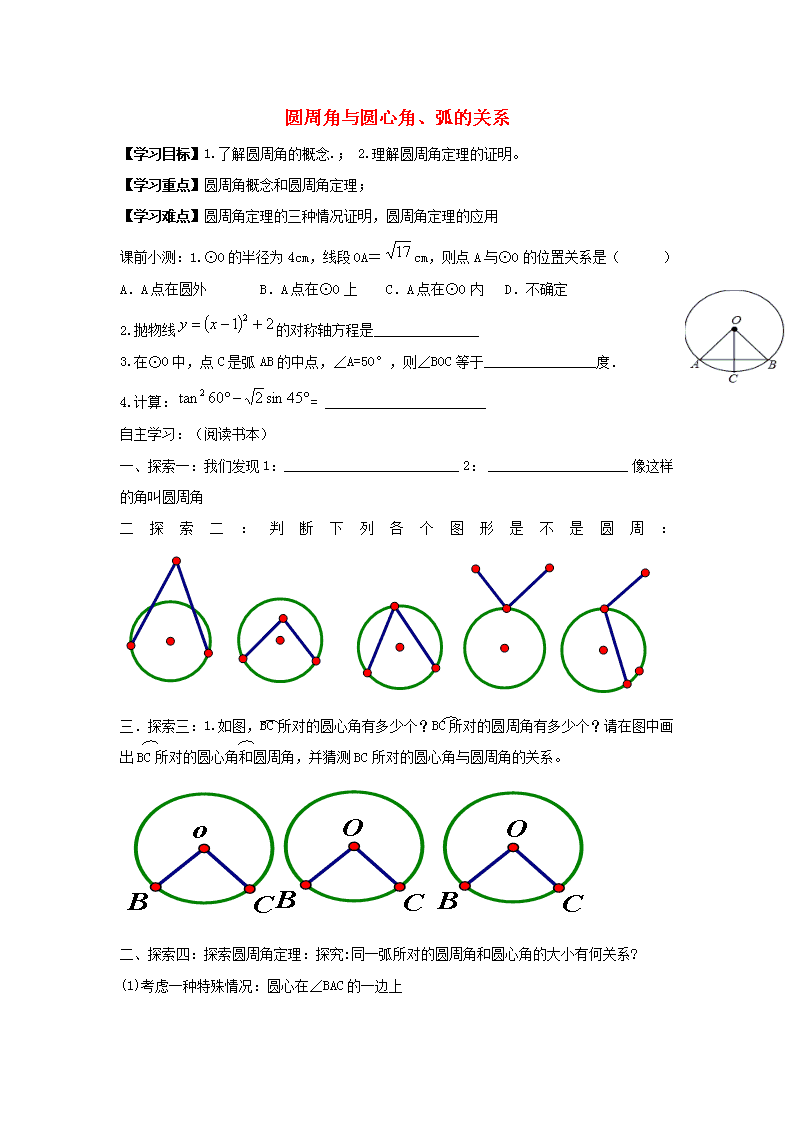
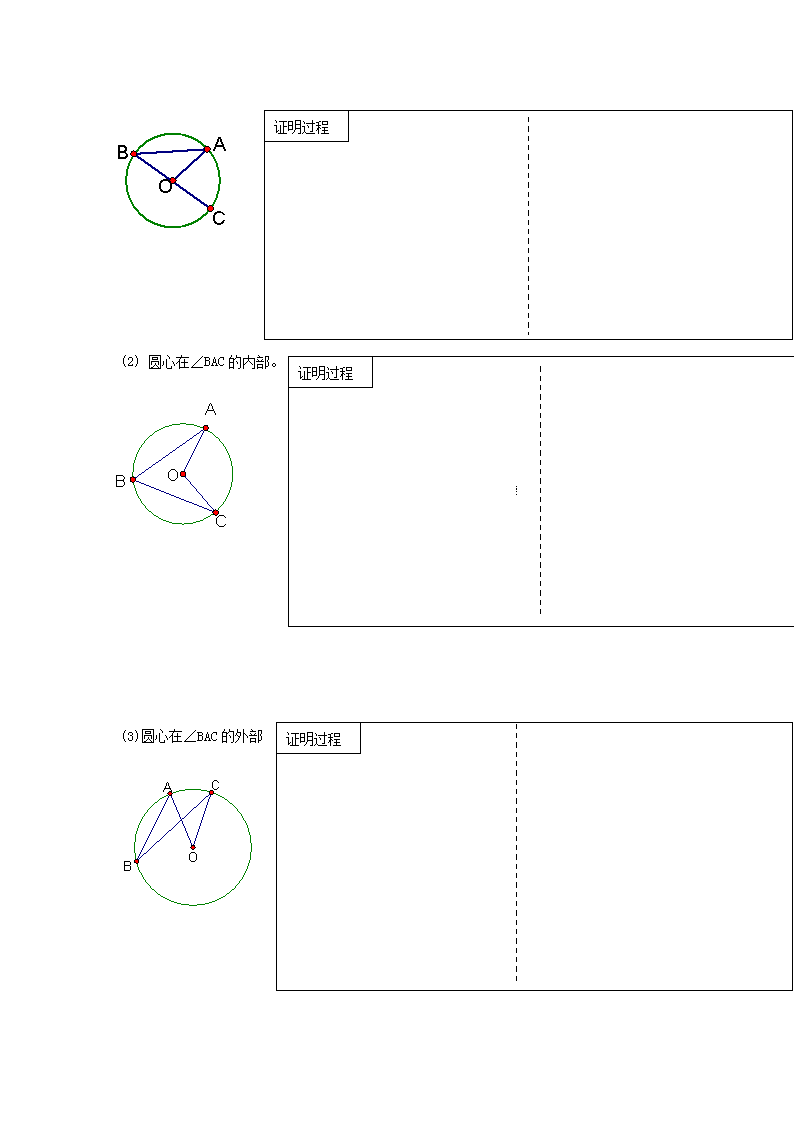
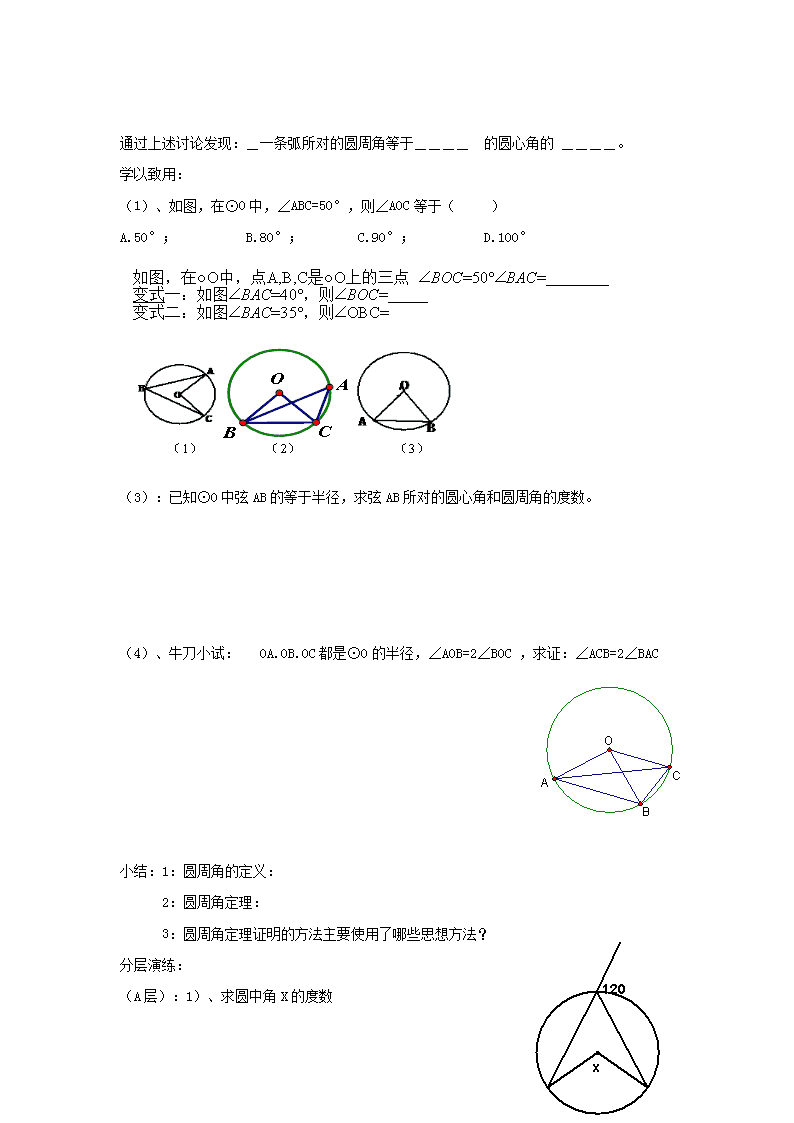
圆周角与圆心角、弧的关系【学习目标】1.了解圆周角的概念.；2.理解圆周角定理的证明。【学习重点】圆周角概念和圆周角定理；【学习难点】圆周角定理的三种情况证明，圆周角定理的应用课前小测：1.⊙O的半径为4cm，线段OA＝cm，则点A与⊙O的位置关系是（）A．A点在圆外B．A点在⊙O上C．A点在⊙O内D．不确定2.抛物线的对称轴方程是_______________3.在⊙O中，点C是弧AB的中点，∠A=50°，则∠BOC等于________________度．4.计算：=_______________________自主学习：（阅读书本）一、探索一：我们发现1：_________________________2：____________________像这样的角叫圆周角二探索二：判断下列各个图形是不是圆周：三．探索三：1.如图，BC所对的圆心角有多少个？BC所对的圆周角有多少个？请在图中画出BC所对的圆心角和圆周角，并猜测BC所对的圆心角与圆周角的关系。二、探索四：探索圆周角定理：探究:同一弧所对的圆周角和圆心角的大小有何关系?(1)考虑一种特殊情况：圆心在∠BAC的一边上n证明过程证明过程(2)圆心在∠BAC的内部。证明过程(3)圆心在∠BAC的外部n通过上述讨论发现：＿一条弧所对的圆周角等于＿＿＿＿的圆心角的＿＿＿＿。学以致用：（1）、如图，在⊙O中，∠ABC=50°，则∠AOC等于（）A.50°；B.80°；C.90°；D.100°（3）：已知⊙O中弦AB的等于半径，求弦AB所对的圆心角和圆周角的度数。（4）、牛刀小试：OA.OB.OC都是⊙O的半径，∠AOB=2∠BOC，求证：∠ACB=2∠BAC小结：1：圆周角的定义：2：圆周角定理：3：圆周角定理证明的方法主要使用了哪些思想方法？分层演练：（A层）：1）、求圆中角X的度数n______________________度______________________度理由______________________________理由_______________________________(ABC层)：如图，在△ABC中，顶点A.B.C都在⊙O上，⊙O的半径R=2，连结OA.OC，sinB=(3/4)求弦AC的长；(B,C层)、半径为R的圆中，有一弦AB分圆周成1：2两部分，则(1)弧AB所对的圆心角的度数是；(2)弧AB所对的圆周角的度数是；(3)弦AB所对的圆心角的度数是；(4)弦AB所对的圆周角的度数是课堂检测：（每题20分）如图，∠AOB=100°，则∠A+∠B等于____n2，如图所示，∠BCD=100°，求∠BOD和∠BAD的大小。3.如图，AB是⊙O的直径，C.D.E都是⊙O上的点，则∠1+∠2=_____.4，如图，在直径为AB的圆中，∠DAB=30°，∠COD=60°，求证：OD//AC5.如图，AB是半圆O的直径，AC=AD，OC=2，∠COB=60°，OE垂直于CD，求OE。