- 32.57 KB
- 2022-04-12 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
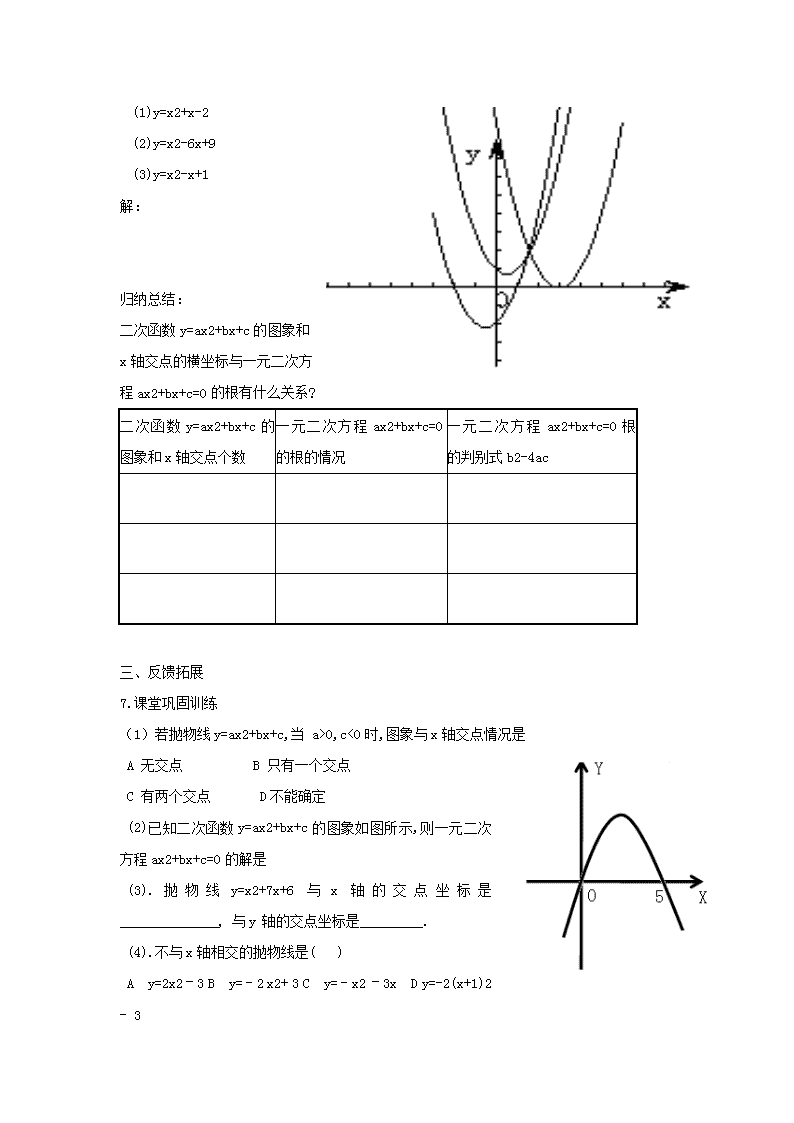
二次函数与一元二次方程学习目标1.巩固一元二次方程和二次函数的基础知识;2.总结出二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系,表述何时方程有两个不等的实根、两个相等的实数和没有实根.3.弄清二次函数与一元二次方程的关系,熟练运用它们之间的关系解决有关问题。教学重点:二次函数与一元二次方程的关系。教学难点:如何运用二次函数与一元二次方程的关系解决问题。【导学流程】一、自主预习:1.创设教学情境2.出示学习目标3.学生自主学习,完成预习题(1)一元二次方程的一般形式()一元二次方程根的情况与b²-4ac的关系:(2).解方程:t2—4t+3=0t2-4t+4.1=0t2-4t+4=04.组内交流质疑二、展示交流:5.小组汇报交流已知二次函数y=-X2+4x的值为3,求自变量x的值.就是求方程_________________的解;反之解方程X2-4x+3=0就是已知二次函数_______________的值为0,求_____________的值。已知函数y=x2-4x+3(1)画出函数的图像:(2)观察图像,当x取哪些值时,函数值为0?6.教师精讲点拨问题:下列二次函数的图象与x轴有公共点吗?如果有,公共点横坐标是多少?当x取公共点的横坐标时,函数的值是多少?由此,你得出相应的一元二次方程的解吗?n(1)y=x2+x-2(2)y=x2-6x+9(3)y=x2-x+1解:归纳总结:二次函数y=ax2+bx+c的图象和x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?二次函数y=ax2+bx+c的图象和x轴交点个数一元二次方程ax2+bx+c=0的根的情况一元二次方程ax2+bx+c=0根的判别式b2-4ac 三、反馈拓展7.课堂巩固训练(1)若抛物线y=ax2+bx+c,当a>0,c<0时,图象与x轴交点情况是A无交点B只有一个交点C有两个交点D不能确定(2)已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0的解是(3).抛物线y=x2+7x+6与x轴的交点坐标是______________,与y轴的交点坐标是_________.(4).不与x轴相交的抛物线是()Ay=2x2–3By=-2x2+3Cy=-x2–3xDy=-2(x+1)2-3n(5)如果关于x的一元二次方程x2-2x+m=0有两个相等的实数根,则m=____,此时抛物线y=x2-2x+m与x轴有____个交点.(6)已知抛物线y=x2–8x+c的顶点在x轴上,则c=____.(7)一元二次方程ax2+bx+c=0的两个根为x1,x2,则抛物线y=ax2+bx+c与x轴的交点坐标是8.教学小结提升:(1)二次函数的图像与一元二次方程的根情况?(2)二次函数的图像与x轴的位置关系?9.达标检测(1)、函数的的图像与x轴的公共点坐标(2)、二次函数的图像与x轴的公共点坐标是(-1,0)和(2,0),并且它经过点(-3,5)求这个函数的表达式。(3).会利用二次函数的图象求一元二次方程的近似解。