七年级数学下册第9章多边形9.1三角形9.1.2三角形的内角和与外角和同步检测（新版）华东师大版 7页

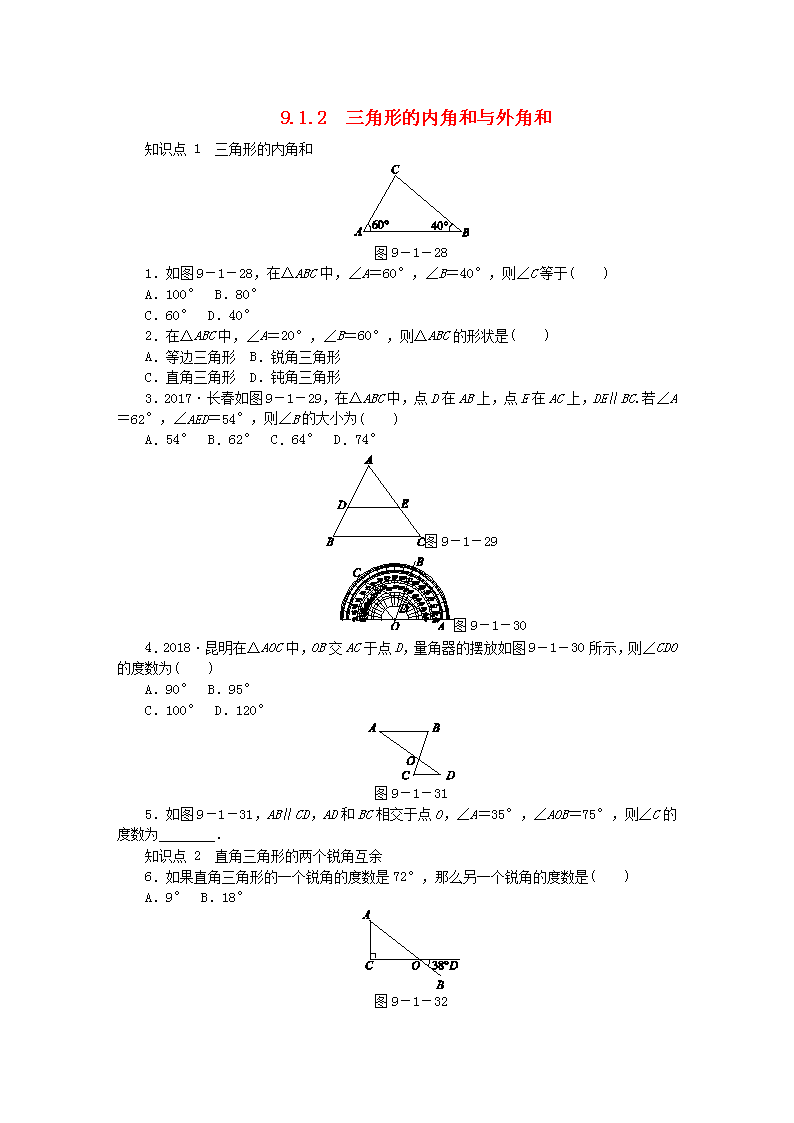
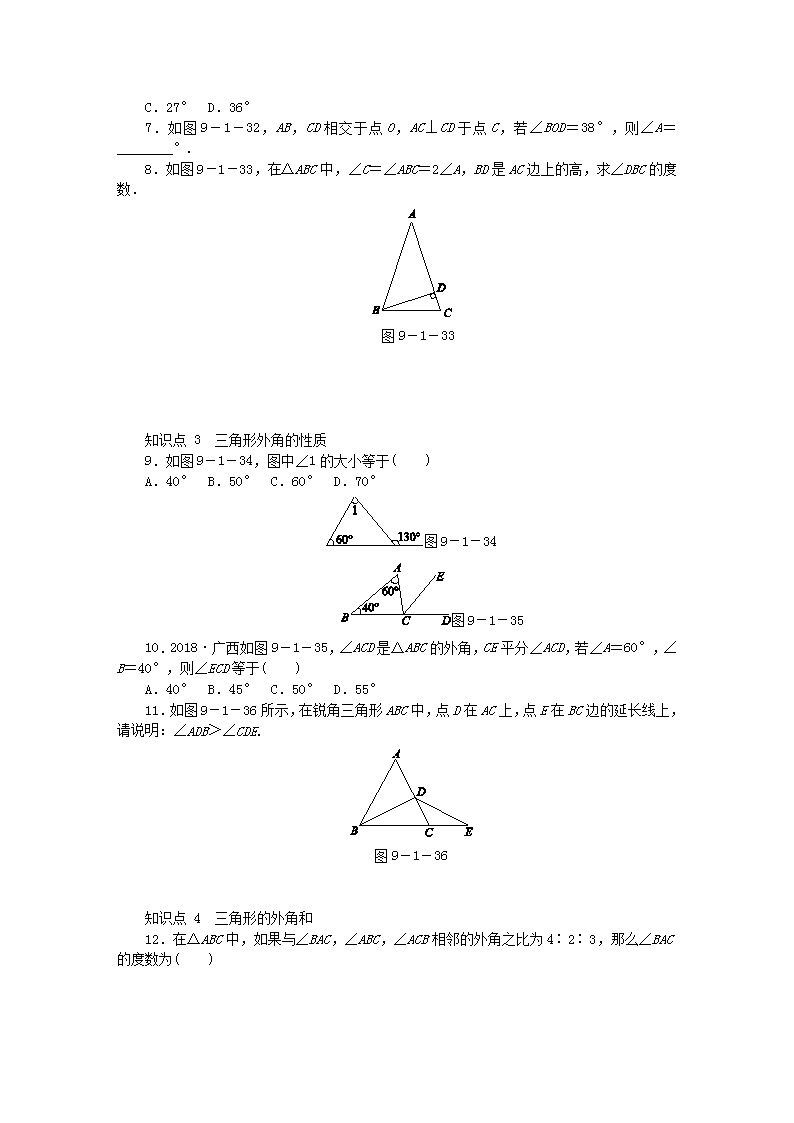
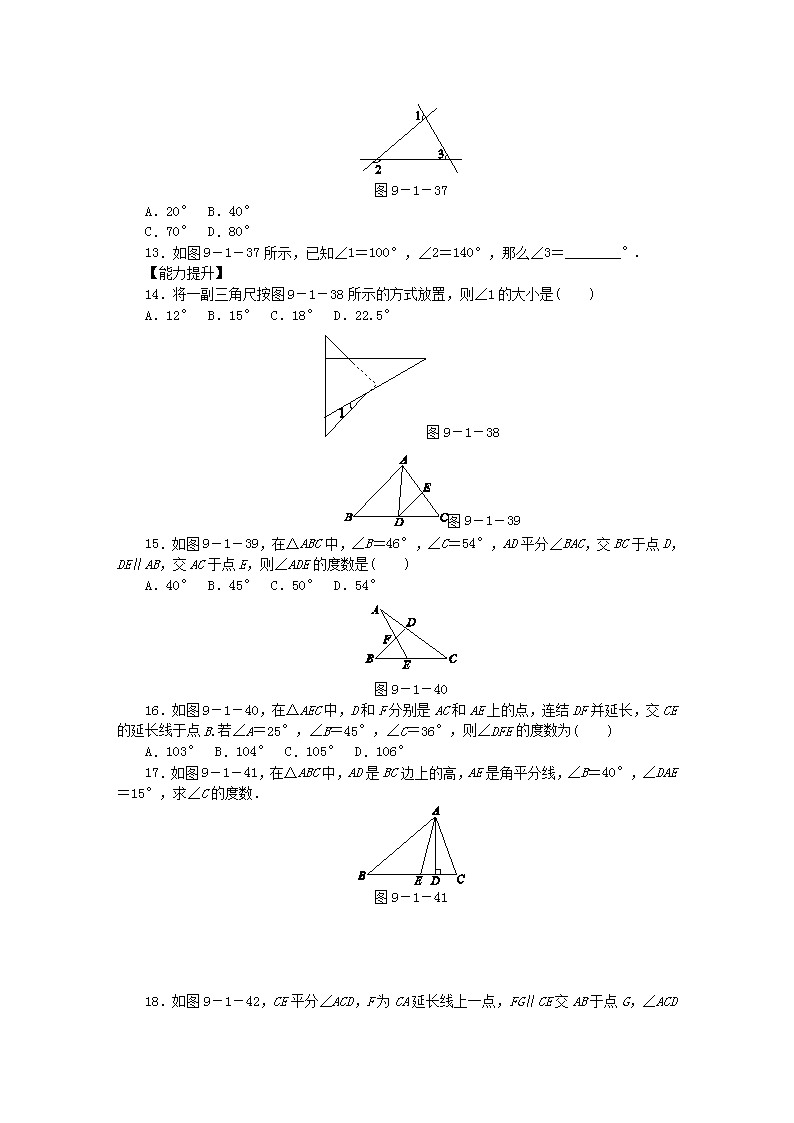
9.1.2　三角形的内角和与外角和知识点1　三角形的内角和图9－1－281．如图9－1－28，在△ABC中，∠A＝60°，∠B＝40°，则∠C等于(　　)A．100°B．80°C．60°D．40°2．在△ABC中，∠A＝20°，∠B＝60°，则△ABC的形状是(　　)A．等边三角形B．锐角三角形C．直角三角形D．钝角三角形3．2017·长春如图9－1－29，在△ABC中，点D在AB上，点E在AC上，DE∥BC.若∠A＝62°，∠AED＝54°，则∠B的大小为(　　)A．54°B．62°C．64°D．74°图9－1－29　　　图9－1－304．2018·昆明在△AOC中，OB交AC于点D，量角器的摆放如图9－1－30所示，则∠CDO的度数为(　　)A．90°B．95°C．100°D．120°图9－1－315．如图9－1－31，AB∥CD，AD和BC相交于点O，∠A＝35°，∠AOB＝75°，则∠C的度数为________．知识点2　直角三角形的两个锐角互余6．如果直角三角形的一个锐角的度数是72°，那么另一个锐角的度数是(　　)A．9°B．18°图9－1－32nC．27°D．36°7．如图9－1－32，AB，CD相交于点O，AC⊥CD于点C，若∠BOD＝38°，则∠A＝________°.8．如图9－1－33，在△ABC中，∠C＝∠ABC＝2∠A，BD是AC边上的高，求∠DBC的度数．　图9－1－33知识点3　三角形外角的性质9．如图9－1－34，图中∠1的大小等于(　　)A．40°B．50°C．60°D．70°图9－1－34　　　图9－1－3510．2018·广西如图9－1－35，∠ACD是△ABC的外角，CE平分∠ACD，若∠A＝60°，∠B＝40°，则∠ECD等于(　　)A．40°B．45°C．50°D．55°11．如图9－1－36所示，在锐角三角形ABC中，点D在AC上，点E在BC边的延长线上，请说明：∠ADB＞∠CDE.图9－1－36知识点4　三角形的外角和12．在△ABC中，如果与∠BAC，∠ABC，∠ACB相邻的外角之比为4∶2∶3，那么∠BAC的度数为(　　)n图9－1－37A．20°B．40°C．70°D．80°13．如图9－1－37所示，已知∠1＝100°，∠2＝140°，那么∠3＝________°.【能力提升】14．将一副三角尺按图9－1－38所示的方式放置，则∠1的大小是(　　)A．12°　B．15°　C．18°　D．22.5°图9－1－38　　　图9－1－3915．如图9－1－39，在△ABC中，∠B＝46°，∠C＝54°，AD平分∠BAC，交BC于点D，DE∥AB，交AC于点E，则∠ADE的度数是(　　)A．40°　B．45°　C．50°　D．54°图9－1－4016．如图9－1－40，在△AEC中，D和F分别是AC和AE上的点，连结DF并延长，交CE的延长线于点B.若∠A＝25°，∠B＝45°，∠C＝36°，则∠DFE的度数为(　　)A．103°B．104°C．105°D．106°17．如图9－1－41，在△ABC中，AD是BC边上的高，AE是角平分线，∠B＝40°，∠DAE＝15°，求∠C的度数．图9－1－4118．如图9－1－42，CE平分∠ACD，F为CA延长线上一点，FG∥CE交AB于点G，∠ACDn＝100°，∠AGF＝20°，求∠B的度数．图9－1－4219.下面是有关△ABC内外角平分线的探究，阅读后按要求作答：探究1：如图9－1－43①，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现：∠BOC＝90°＋∠A(不要求证明)．探究2：如图9－1－43②，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的数量关系，请说明理由．探究3：如图9－1－43③，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的数量关系？结论：______________．(只写结论，不需证明)图9－1－43n教师详解详析1．B　[解析]由三角形内角和定理得∠C＝180°－∠A－∠B＝80°，故选B.2．D　[解析]∵∠A＝20°，∠B＝60°，∴∠C＝180°－∠A－∠B＝180°－20°－60°＝100°，∴△ABC是钝角三角形．故选D.3．C　[解析]∵DE∥BC，∴∠C＝∠AED＝54°.∵∠A＝62°，∴∠B＝180°－∠A－∠C＝64°，故选C.4．B5．70°　[解析]∵∠A＝35°，∠AOB＝75°，∠A＋∠B＋∠AOB＝180°，∴∠B＝180°－35°－75°＝70°.又∵AB∥CD，∴∠C＝∠B＝70°.6．B7．52　[解析]观察图形知∠BOD与∠AOC是对顶角，∴∠AOC＝∠BOD＝38°.又在Rt△ACO中，两锐角互余，∴∠A＝90°－38°＝52°.8．解：∵∠C＝∠ABC＝2∠A，∴∠C＋∠ABC＋∠A＝5∠A＝180°，∴∠A＝36°，∴∠C＝2∠A＝72°.又∵BD是AC边上的高，∴∠DBC＝90°－∠C＝18°.9．D10．C11．解：∵∠ADB是△BCD的一个外角，∴∠ADB＞∠BCD.∵∠BCD是△CDE的一个外角，∴∠BCD＞∠CDE，∴∠ADB＞∠CDE.12．A　[解析]∵与∠BAC，∠ABC，∠ACB相邻的外角之比为4∶2∶3，∴可设与∠BAC，∠ABC，∠ACB相邻的外角分别为4x，2x，3x，则有4x＋2x＋3x＝360°，解得x＝40°，则4x＝160°，∴∠BAC＝180°－160°＝20°.故选A.13．60　[解析]根据三角形的外角和为360°，求出∠3的补角，进而求出∠3.14．B　15．A　[解析]∵∠B＝46°，∠C＝54°，∴∠BAC＝180°－∠B－∠C＝180°－46°－54°＝80°.∵AD平分∠BAC，∴∠BAD＝∠BAC＝×80°＝40°.∵DE∥AB，∴∠ADE＝∠BAD＝40°.16．D　[解析]∵∠FEB是△AEC的一个外角，∴∠FEB＝∠A＋∠C＝61°.∵∠DFE是△BFE的一个外角，∴∠DFE＝∠B＋∠FEB＝106°.故选D.17．解：∵AD是BC边上的高，∴∠ADE＝90°.n∵∠ADE＋∠AED＋∠DAE＝180°，∴∠AED＝180°－∠ADE－∠DAE＝180°－90°－15°＝75°.∵∠B＋∠BAE＝∠AED，∴∠BAE＝∠AED－∠B＝75°－40°＝35°.∵AE是△ABC的角平分线，∴∠BAC＝2∠BAE＝2×35°＝70°.∵∠B＋∠BAC＋∠C＝180°，∴∠C＝180°－∠B－∠BAC＝180°－40°－70°＝70°.18．解：∵CE平分∠ACD，∠ACD＝100°，∴∠ACE＝∠ACD＝×100°＝50°.∵FG∥CE，∴∠AFG＝∠ACE＝50°.在△AFG中，∠BAC＝∠AFG＋∠AGF＝50°＋20°＝70°.又∵∠ACB＝180°－∠ACD＝180°－100°＝80°，∴∠B＝180°－∠BAC－∠ACB＝180°－70°－80°＝30°.19.[解析]探究2：根据提供的信息，根据三角形的一个外角等于与它不相邻的两个内角的和，用∠A与∠1表示出∠2，再利用∠2与∠1表示出∠BOC，然后整理即可得到∠BOC与∠A的关系；探究3：根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB，然后根据三角形的内角和定理列式整理即可得解．解：探究2：∠BOC＝∠A.理由如下：如图．∵BO和CO分别是∠ABC和∠ACD的平分线，∴∠1＝∠ABC，∠2＝∠ACD.又∵∠ACD是△ABC的一个外角，∴∠ACD＝∠A＋∠ABC，∴∠2＝(∠A＋∠ABC)＝∠A＋∠1.∵∠2是△BOC的一个外角，∴∠BOC＝∠2－∠1＝∠A＋∠1－∠1＝∠A.探究3：∠BOC＝90°－∠A.理由如下：∵∠OBC＝(∠A＋∠ACB)，∠OCB＝(∠A＋∠ABC)，∴∠BOC＝180°－∠OBC－∠OCB＝180°－(∠A＋∠ACB)－(∠A＋∠ABC)＝180°－∠nA－(∠A＋∠ABC＋∠ACB)＝180°－∠A－×180°＝90°－∠A，故结论是∠BOC＝90°－∠A.