江西省新余市第四中学2019届高考数学全真模拟考试试题文 13页

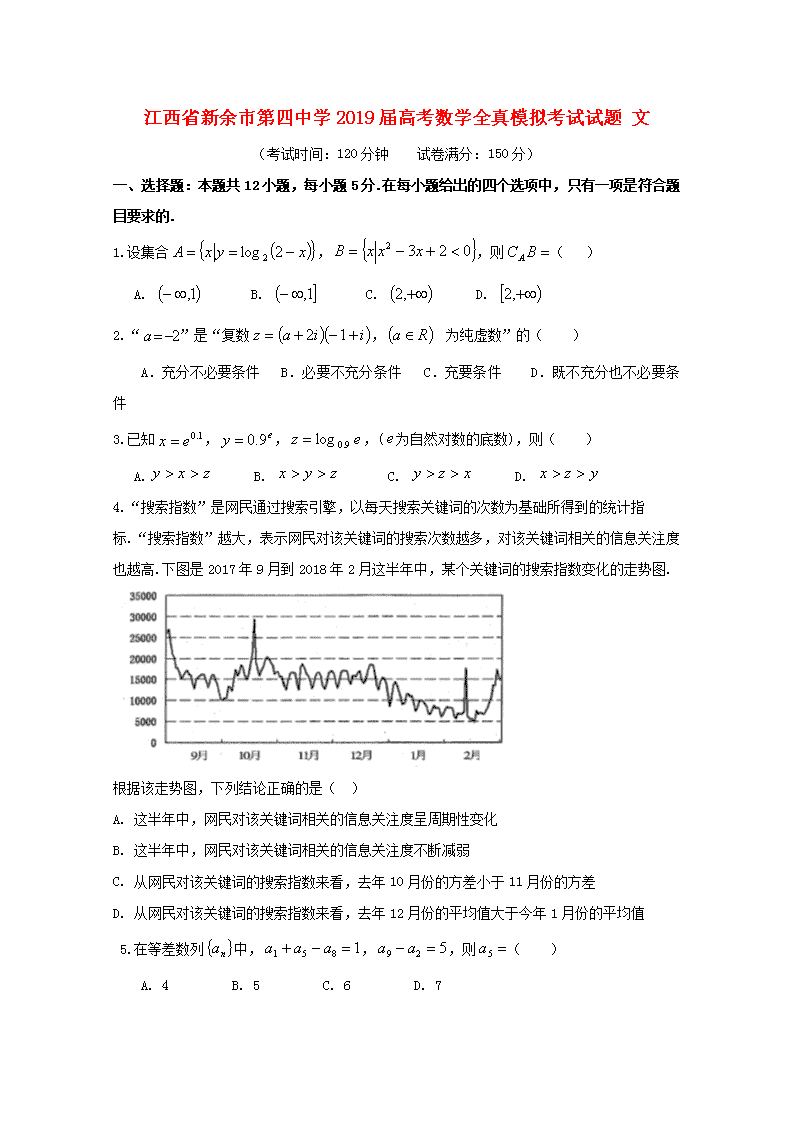
江西省新余市第四中学2019届高考数学全真模拟考试试题文（考试时间：120分钟试卷满分：150分）一、选择题：本题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合，，则（）A.B.C.D.2.“”是“复数，为纯虚数”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3.已知，，，(为自然对数的底数)，则（）A.B.C.D.4.“搜索指数”是网民通过搜索引擎，以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大，表示网民对该关键词的搜索次数越多，对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中，某个关键词的搜索指数变化的走势图.根据该走势图，下列结论正确的是（）A.这半年中，网民对该关键词相关的信息关注度呈周期性变化B.这半年中，网民对该关键词相关的信息关注度不断减弱C.从网民对该关键词的搜索指数来看，去年10月份的方差小于11月份的方差D.从网民对该关键词的搜索指数来看，去年12月份的平均值大于今年1月份的平均值5.在等差数列中，，，则（）A.4B.5C.6D.7n6．已知向量与的夹角为，，，则在方向上的投影为()A．B．C．D．7.执行如图所示的框图，如果输出，则的值为（）A.1B.2C.3D.48.已知,，且，则（）A.B.C.D.9.已知函数是定义在上的奇函数，且在上单调递增，则满足的的取值范围是（）A.B.C.D.10.过双曲线左焦点，作圆的切线，切点为，延长交双曲线右支于点，若，则双曲线的离心率为（）A.B.C.D.11．一个空间几何体的三视图如图所示，俯视图为正三角形，则它的外接球的表面积为(）A.B.C.D.12.已知函数，若且满足，则的取值范围是（）nA.B.C.D.二、填空题：本大题共4小题，每小题5分.把答案填在答题卡的相应位置.13.已知函数.14.若满足约束条件则的最大值为__________．15.中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹，用于装点生活或配合其他民俗活动的民间艺术，蕴涵了极致的数学美和丰富的传统文化信息。现有一幅剪纸的设计图，其中的个小圆均过正方形的中心，且内切于正方形的两邻边。若在正方形内随机取一点，则该点取自黑色部分的概率为__________．16.已知的内角的对边分别为且满足当时，的面积等于.三、解答题：解答应写出文字说明、证明过程或演算步骤．17.（12分）已知数列为等差数列，，且满足，数列满足，．（1）求数列的通项公式；（2）若，求数列的前n项和．18.（12分）改革开放以来，伴随着我国经济持续增长，户均家庭教育投入（户均家庭教育投入是指一个家庭对家庭成员教育投入的总和）也在不断提高，我国某地区2012年至2018年户均家庭教育投入（单位：千元）的数据如下表：年份2012201320142015201620172018年份代号1234567户均家庭教育投入3.43.84.14.95.35.76.4（1）求关于的线性回归方程；n（2）利用（1）中的回归方程，分析2012年至2018年该地区户均家庭教育投入的变化情况，并预测2019年该地区户均家庭教育投入是多少。附：回归直线的斜率和截距的最小二乘法估计公式分别为：19.（12分）斜三棱柱中，底面是边长为2的正三角形，，.（1）证明：平面平面；（2）求四棱锥的体积.20.（12分）已知斜率为1的直线交抛物线于两点，且弦中点的纵坐标为2.（1）求抛物线的标准方程；（2）记点，过点作两条直线分别交抛物线于不同于点）两点，且的平分线与轴垂直，求证：直线的斜率为定值。21．（12分）设函数．（1）当时，求的极值；（2）若的定义域为，判断是否存在极值．若存在，试求的取值范围；否则，请说明理由．请考生在第22、23题中任选一题作答.注意：只能做所选定的题目，如果多做，则按所做的第一个题目计分，作答时，请用2B铅笔在答题卡上，将所选题号对应的方框涂黑.22.在平面直角坐标系中，曲线的参数方程为（为参数），以原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为曲线的公共点为。n（Ⅰ）求直线的斜率；（Ⅱ）若点分别为曲线，上的动点，当取最大值时，求四边形的面积.23.设的最小值为.（Ⅰ）求的值；（Ⅱ）设,求的最小值.n新余四中2019届高考年级全真模拟数学（文科）答案一、选择题：1——5BCBDC6——10BCACC11——12BA二、填空题：13.-214.115.16.三、解答题：17.解：(1)由等差数列的性质可得：，解得．………………………2分数列满足，可得：数列是等比数列，公比为2．∵．∴，解得．………………………4分∴．………………………6分(2)若，∴数列的前n项和，，∴，………………………10分可得．………………………12分19（1），，由余弦定理：即或故取中点，连接，是边长为的正三角形，可得：，由得到又为中点，且n又，平面平面平面平面（2）由（1）20、21.解：（1）定义域为当时函数，，……………5分（2）令即令，则对称轴……………6分①当，即时恒成立在无极值点.……………7分②当，即，………9分当时，恒成立，无极值.………10分当时，有n存在，使得，存在，使得，当时，当时，，当时，，当时，，有极值综上所述，…………12分22.（Ⅰ）消去参数α得曲线C1的普通方程C1：x2+y2﹣2y=0．…（1）将曲线C2：ρ=4cosθ化为直角坐标方程得x2+y2﹣4x=0．…（2）由（1）﹣（2）化简得y=2x，即为直线AB的方程，故直线AB的斜率为2；（Ⅱ）由C1：x2+y2﹣2y=0知曲线C1是以C1（0，1）为圆心，半径为1的圆，由C2：x2+y2﹣4x=0知曲线C2：是以C2（2，0）为圆心，半径为2的圆．∵|CD|≤|CC1|+|C1C2|+|DC2|，∴当|CD|取最大值时，圆心C1，C2在直线CD上，∴直线CD（即直线C1C2）的方程为：2x+y=2．∵O到直线CD的距离为，即|AB|=又此时|CD|=|C1C2|+1+2=3+，∴四边形ACBD的面积．23.（Ⅰ）当时，当时，;当时，当时，取得最小值（Ⅱ）由题意知当且仅当时，即等号成立，的最小值为.n新余四中2019届高考年级全真模拟数学（文科）答案一、选择题：1——5BCBDC6——10BCACC11——12BA二、填空题：13．114.115.16.三、解答题：17.解：(1)由等差数列的性质可得：，解得．………………………2分数列满足，可得：数列是等比数列，公比为2．∵．∴，解得．………………………4分∴．………………………6分(2)若，∴数列的前n项和，，∴，………………………10分可得．………………………12分18.（1）由所给数据计算得：………1分………2分………3分……n……5分，…………6分所求回归方程为。…………8分（2）由（1）知,故2012年至2018年该地区户均家庭教育投入逐年增加，平均每年增加0.5千克。…………10分将2019年的年份代号代入（1）中的回归方程，得。故预测该地区2019年户均家庭教育投入为6.8千元。…………12分19．（1），，由余弦定理：即或故取中点，连接，是边长为的正三角形，可得：，由得到又为中点，且又，平面平面平面平面………6分（2）由（1）………12分20、解：(1)设，中点为，则有两式相减得，即得，由题意知，所以，抛物线方程为。………5分（2）设直线为：（由题意知直线斜率一定不为0）n联立得，由得。且。………6分由题意知，即（*），………8分将代入（*）并化简得由韦达定理得，………10分即。当时该等式恒成立，所以直线的斜率为，即为-1.………12分21.解：（1）定义域为当时函数，，……………5分（2）令即令，则对称轴……………6分①当，即时恒成立n在无极值点.……………7分①当，即，………9分当时，恒成立，无极值.………10分当时，有存在，使得，存在，使得，当时，当时，，当时，，当时，，有极值综上所述，…………12分22.（Ⅰ）消去参数α得曲线C1的普通方程C1：x2+y2﹣2y=0．…（1）将曲线C2：ρ=4cosθ化为直角坐标方程得x2+y2﹣4x=0．…（2）由（1）﹣（2）化简得y=2x，即为直线AB的方程，故直线AB的斜率为2；（Ⅱ）由C1：x2+y2﹣2y=0知曲线C1是以C1（0，1）为圆心，半径为1的圆，由C2：x2+y2﹣4x=0知曲线C2：是以C2（2，0）为圆心，半径为2的圆．∵|CD|≤|CC1|+|C1C2|+|DC2|，∴当|CD|取最大值时，圆心C1，C2在直线CD上，∴直线CD（即直线C1C2）的方程为：2x+y=2．∵O到直线CD的距离为，即|AB|=又此时|CD|=|C1C2|+1+2=3+，∴四边形ACBD的面积．23.（Ⅰ）当时，当时，;当时，当时，取得最小值（Ⅱ）由题意知n当且仅当时，即等号成立，的最小值为.