- 55.23 KB
- 2022-04-12 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
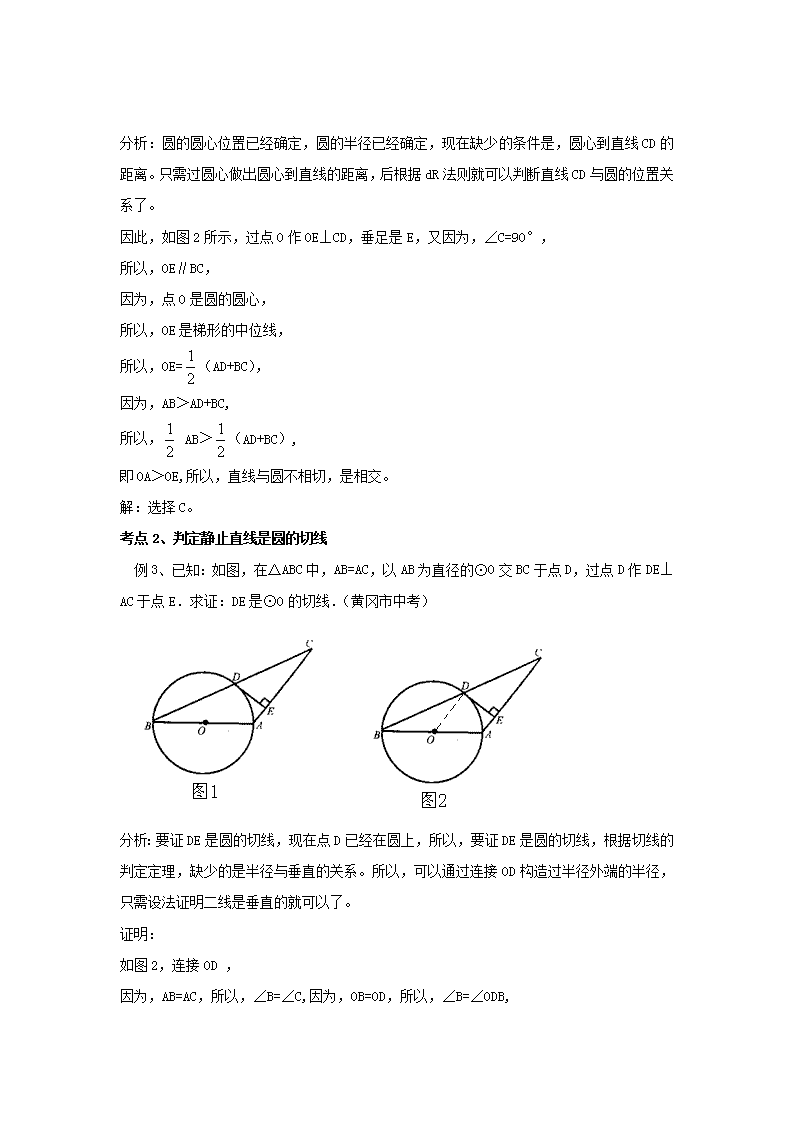
直线与圆相切一、知识解读:判定直线与圆相切的方法:1、定义法:直线和有且只有一个公共点,就说直线与圆相切。2、d、R法则:设圆心到直线的距离是d,圆的半径是R,则当d=R时,直线与圆相切。3、切线的判定定理:过半径的外端,并且垂直于这条半径的直线,是圆的切线。在应用判定定理时,关键有两个:一是直线要经过圆上的某点,而是直线与过该点的半径垂直。必要时,要构造半径作为解题的辅助线。二、考点例析:考点1、考d、R法则例1、在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定()A.与轴相离、与轴相切B.与轴、轴都相离C.与轴相切、与轴相离 D.与轴、轴都相切(南昌市中考)分析:根据坐标系的知识,知道,圆心到y轴的距离是dy=2,到x轴的距离是dx=3,由于圆的半径R=2,所以,dy=R,所以,y轴与圆相切,这样,我们就可以排除B和D;因为,dx=3>R=2,所以,x轴与圆相离,因此,选项A是正确的。解:选则A。例2、如图1所示,在直角梯形中,,,且,是⊙O的直径,则直线与⊙O的位置关系为()A.相离B.相切C.相交D.无法确定(内江市中考)n分析:圆的圆心位置已经确定,圆的半径已经确定,现在缺少的条件是,圆心到直线CD的距离。只需过圆心做出圆心到直线的距离,后根据dR法则就可以判断直线CD与圆的位置关系了。因此,如图2所示,过点O作OE⊥CD,垂足是E,又因为,∠C=90°,所以,OE∥BC,因为,点O是圆的圆心,所以,OE是梯形的中位线,所以,OE=(AD+BC),因为,AB>AD+BC,所以,AB>(AD+BC),即OA>OE,所以,直线与圆不相切,是相交。解:选择C。考点2、判定静止直线是圆的切线例3、已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.求证:DE是⊙O的切线.(黄冈市中考)分析:要证DE是圆的切线,现在点D已经在圆上,所以,要证DE是圆的切线,根据切线的判定定理,缺少的是半径与垂直的关系。所以,可以通过连接OD构造过半径外端的半径,只需设法证明二线是垂直的就可以了。证明:如图2,连接OD,因为,AB=AC,所以,∠B=∠C,因为,OB=OD,所以,∠B=∠ODB,n所以,∠C=∠ODB,所以,OD∥AC,因为,DE⊥AC,所以,DE⊥OD,所以,DE是圆的切线。例4、如图3所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.求证:DE为⊙O的切线;(恩施自治州中考改编)分析:连接OD,关键证明DE⊥OD。证明:如图4,连接OD,因为,OA=OB,DC=BD,所以,OD∥AC,因为,DE⊥AC,所以,DE⊥OD,所以,DE是圆的切线。考点3、判定运动直线是圆的切线例5、如图所示,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以cm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为▲s时,BP与⊙O相切.n分析:点P运动到两个位置时,直线BP是圆的切线,一个是OP⊥BP时,一个是OD⊥BP时,分别计算出点P行驶的弧长,除以速度就是所用的时间。解:如图6所示,连接OP、OD,因为,AB=OA=OP,所以,∠PBO=30°,所以,∠POB=60°,所以,PA弧的长为:=π(cm),根据圆的对称性,知道AD劣的长为π(cm),因为,圆的周长是6π(cm),所以,优弧AD的长为5π(cm),所以,点P运动的时间分别是:π÷π=1秒,或5π÷π=5秒。所以,点P运动1秒或者5秒时,直线BP是圆的切线。