- 450.76 KB
- 2022-04-12 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
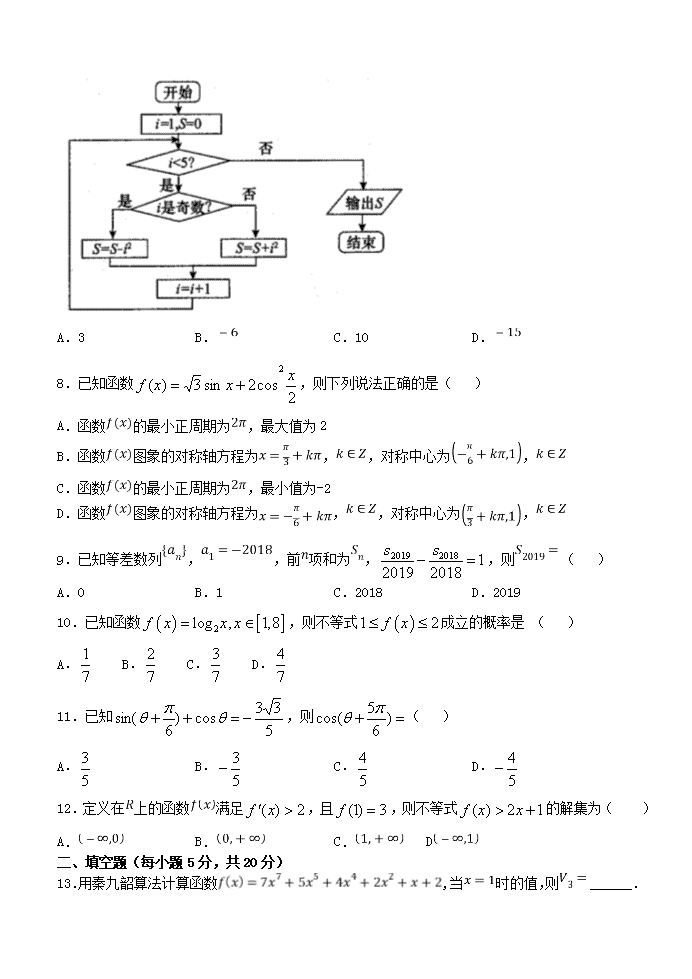
天水一中高二级2018-2019学年第二学期第二学段考试数学试题(文)一、单选题(每小题5分,共60分)1.已知集合,集合,则( )A.B.C.D.2.若为纯虚数,则实数的值为()A.-2B.2C.3D.-33.若,则a、b、c的大小关系是( )A.B.C.D.4.函数的图象大致是()A.B.C.D.5.已知向量满足,则与的夹角为()A.B.C.D.6.在等比数列中,若,且成等差数列,则其前项和为()A.B.C.D.7.执行如图所示的程序框图,输出的值为()nA.3B.C.10D.8.已知函数,则下列说法正确的是()A.函数的最小正周期为,最大值为2B.函数图象的对称轴方程为,,对称中心为,C.函数的最小正周期为,最小值为-2D.函数图象的对称轴方程为,,对称中心为,9.已知等差数列,,前项和为,,则()A.0B.1C.2018D.201910.已知函数,则不等式成立的概率是()A.B.C.D.11.已知,则()A.B.C.D.12.定义在上的函数满足,且,则不等式的解集为()A.B.C.D二、填空题(每小题5分,共20分)13.用秦九韶算法计算函数,当时的值,则______.n14.已知不等式的解集为或,则______.15.已知数列的前项和为,,且,则当取得最大值时,n=__________.16.的内角的对边分别为,若,,则的外接圆的面积为______.三、解答题(共70分.选做题10分,其余每题各12分,写出必要的解答过程)17.已知等比数列的各项均为正数,且.(1)求数列的通项公式;(2)设.求的前项和18.在中,角所对的边分别为,且.(Ⅰ)求角;(Ⅱ)若为的中点,,求的面积.19.为迎接年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了名学生,将他们的比赛成绩(满分为分)分为组:,,,,,,得到如图所示的频率分布直方图.(Ⅰ)求的值;(Ⅱ)记表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于分”,估计的概率;(Ⅲ)在抽取的名学生中,规定:比赛成绩不低于分为“优秀”,比赛成绩低于分为“非优秀”.请将下面的列联表补充完整,并判断是否有的把握认为“比赛成绩是否优秀与性别有关”?优秀非优秀合计男生女生合计参考公式及数据:,.n20.已知抛物线的顶点为原点,关于轴对称,且过点.(1)求抛物线的方程;(2)已知,若直线与抛物线交于,两点,记直线,的斜率分别为,,求证:为定值.21.已知函数.(1)若函数的一个极值点为,求函数的极值;(2)讨论的单调性.22.(10分)直角坐标系中,曲线的参数方程为;以为极点,以轴的非负半轴为极轴建立极坐标系,直线的极坐标方程为,曲线.(1)求曲线的普通方程和极坐标方程;(2)已知直线与曲线和曲线分别交于和两点(均异于点),求线段的长.23.(10分)已知函数.(1)解不等式;(2)设,若对任意,都有,使得成立,求实数的取值范围.n参考答案1.C2.D3.B4.D5.B6.B7.C8.B9.A10.B11.A12.C13.1614.315.716.17.(1);(2)(1)设数列的公比为,由,可得,则,数列各项均为正数,,即,由可得.解得,.(2)由(1)知,,.18.(1)(2)(Ⅰ)(Ⅱ)设解得:19.(Ⅰ)(Ⅱ)(Ⅲ)见解析n(Ⅰ)由题可得,解得.(Ⅱ)由(Ⅰ)知,则比赛成绩不低于分的频率为,故从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于分的概率约为.(Ⅲ)由(Ⅱ)知,在抽取的名学生中,比赛成绩优秀的有人,由此可得完整的列联表:优秀非优秀合计男生女生合计所以的观测值,所以没有的把握认为“比赛成绩是否优秀与性别有关”.20.(1)(2)见证明解:(1)设抛物线为,将代入得,则抛物线的方程为;(2)设,,由得,则,,,∴n,∴.所以为定值.21.(1)的极小值为,没有极大值(2)见解析解:(1),∵是函数的一个极值点,∴,∴∴∴时,;时,,∴的单调减区间为,单调增区间为,∴的极小值为,没有极大值,(2)(x>0),当时,对,是减函数,当,由,得,,显然,且当时,是减函数;时,,是增函数,综上,时,的单调减区间为,没有增区间,时,的单调减区间为,单调增区间为.22.(Ⅰ)因为曲线的参数方程为(为参数),所以的普通方程为①,在极坐标系中,将代入①得,化简得,的极坐标方程为:②.(Ⅱ)因为直线的极坐标方程为(),且直线与曲线和和曲线分别交于,,可设,,n将代入②得,将代入曲线得.所以.23.(I)或;(II)(I)不等式等价于,①当时,原不等式即为,解得,所以;②当时,原不等式即为,解得,所以;③当时,原不等式即为,解得,所以;所以不等式的解集为或.(II)对任意,都有,使得成立,则.因为,当且仅当时取等号,又,所以从而或,所以实数的取值范围.