- 231.93 KB
- 2022-04-12 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
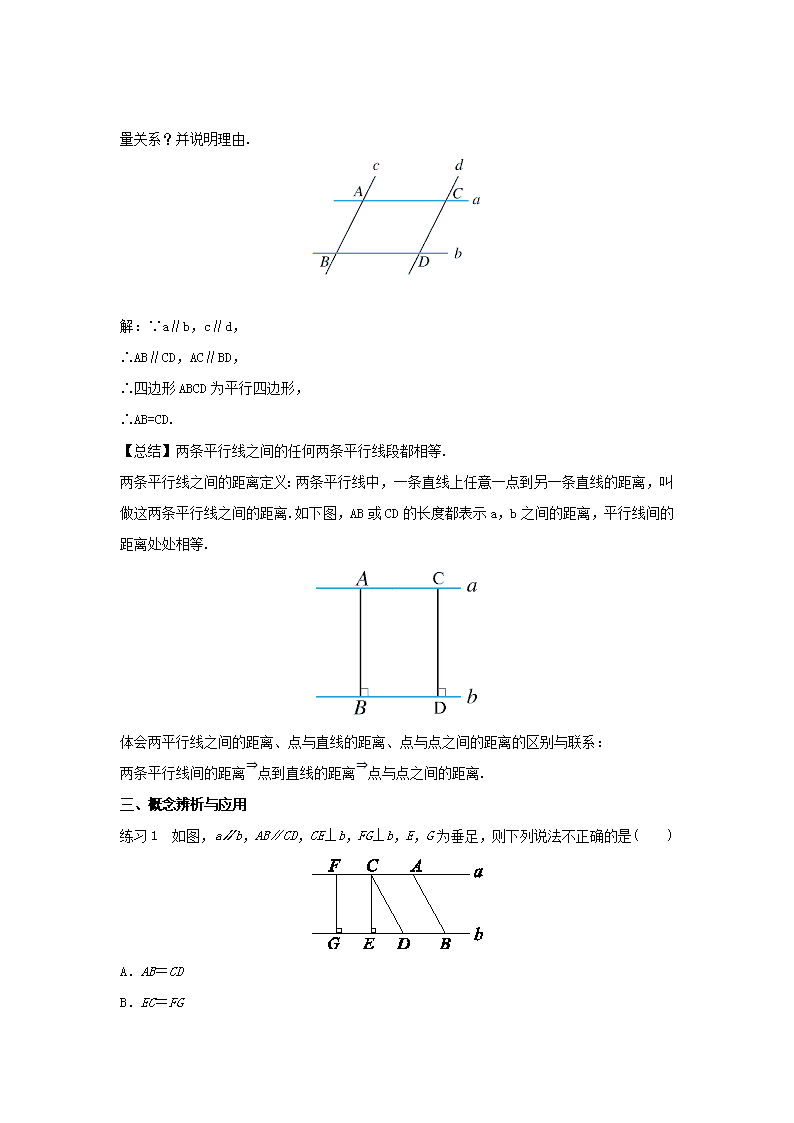
第十八章平行四边形18.1平行四边形平行四边形的性质(第2课时)◆教材分析本课学习平行线间的距离,进一步探索和证明对角线的性质.◆教学目标1.了解平行线间距离的概念;2.掌握平行四边形对角线互相平分的性质;3.经历对平行四边形性质的猜想与证明的过程,渗透转化思想,体会图形性质探究的一般思路.◆教学重难点◆平行四边形对角线性质的证明和应用.◆课前准备◆课件,多媒体素材.◆教学过程一、知识回顾在□ABCD中,ABCD,ADBC;∠A∠C,∠B∠D.二、观察抽象,形成概念如图,a∥b,c∥d,c,d与a,b分别相交于A,B,C,D四点,请探究AB与CD的数n量关系?并说明理由.解:∵a∥b,c∥d,∴AB∥CD,AC∥BD,∴四边形ABCD为平行四边形,∴AB=CD.【总结】两条平行线之间的任何两条平行线段都相等.两条平行线之间的距离定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.如下图,AB或CD的长度都表示a,b之间的距离,平行线间的距离处处相等.体会两平行线之间的距离、点与直线的距离、点与点之间的距离的区别与联系:两条平行线间的距离⇒点到直线的距离⇒点与点之间的距离.三、概念辨析与应用练习1如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E,G为垂足,则下列说法不正确的是()A.AB=CDB.EC=FGnC.A,B两点的距离就是线段AB的长度D.a与b的距离就是线段CD的长度练习2如图,已知直线a∥b,点C,D在直线a上,点A,B在直线b上,线段BC,AD相交于点E,写出图中面积相等的三角形:.四、情境导入一位饱经沧桑的老人经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地.由于年迈体弱,他决定把这块土地平分给他的四个孩子,他是这样分的:当四个孩子看到时,争论不休,都认为自己分的地少,同学们:老人这样分地合理吗?师:合理不合理关键看平行四边形的对角线有什么性质,这节课我们就来继续研究平行四边形的性质.设计意图:用实际问题(置疑)创设情境导入新课,既激发了学生学习新知识的积极性和主动性,又让学生感受到数学知识来源于生活,又服务于生活.五、概括证明,探究性质注:此图片是动画缩略图,拖动图形构造不同形状的平行四边形,观察其对角线的情况,如需使用此资源,请插入动画“【知识探究】探究平行四边形对角线的性质”.探究证明:平行四边形的对角线互相平分.已知:如图,□ABCD的两条对角线AC与BD相交于点O.n求证:OA=OC,OB=OD.证明:∵四边形ABCD是平行四边形,∴AB=CD(平行四边形的对边相等),AB∥CD(平行四边形的定义).∴∠BAO=∠DCO,∠ABO=∠CDO.∴△ABO≌△CDO(ASA).∴OA=OC,OB=OD.定理:平行四边形的对角线互相平分.六、应用知识,解决问题例1如图,□ABCD的对角线AC,BD交于点O,若AD=8,BD=12,AC=6,则△OBC的周长为.例2若□ABCD的周长为100cm,两条对角线相交于点O,△AOB的周长比△BOC的周长多10cm,则AB=________cm,BC=________cm.例3如图,在□ABCD中,AB=10,AD=8,AC⊥BC.求BC,CD,AC,OA的长,以及□ABCD的面积.解:∵四边形ABCD是平行四边形,∴BC=AD=8,CD=AB=10.n∵AC⊥BC,∴△ABC是直角三角形.根据勾股定理,AC===6.又∵OA=OC,∴OA=AC=3,S□ABCD=BC·AC=8×6=48.例4在□ABCD中,对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F.求证:OE=OF.证明:∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD,∴∠EAO=∠FCO,∠AEO=∠CFO.∴△AOE≌△COF(AAS).∴OE=OF.七、课堂小结1.平行四边形的边、角和对角线各有什么性质?Ø平行四边形的对边相等且平行;Ø平行四边形的对角相等;Ø平行四边形的对角线互相平分.2.研究平行四边形常用的方法是什么?研究平行四边形常常把它转化为三角形问题,体现了化归的数学思想.3.什么是两条平行线之间的距离?