小学数学-数阵图课件 23页

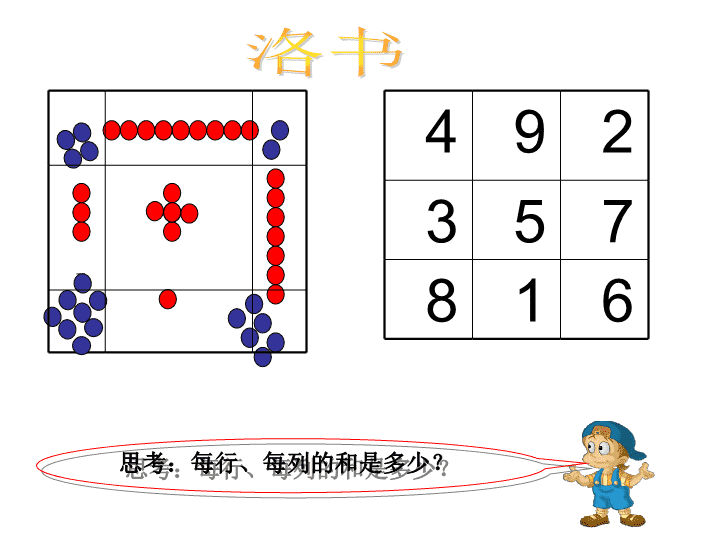
数阵图\n公元前2000多年，我国部分地区洪水泛滥，有个名叫禹的人负责治理水灾的事(历史上称他为夏禹)。传说一次在洛水里浮起一只大乌龟，背上有一幅奇特的图案。这就是著名的“洛书”。你发现了什么？神奇的书\n492357816思考：每行、每列的和是多少？洛书\n例1铺垫（辐射型数阵图）数字精灵1、3、5、7、9分别要站在圆圈中，并且每条线上的3个数的和都相等。数字精灵们分别应该站在哪个圆圈中？思考：你觉得先填哪个圆圈最重要？\n辐射图，有技巧。中间数，填中间，首尾成双面对面。你还有不同的填法吗？真棒！\n思考：想一想，要使每条线上3个数的和相等，你还有别的填法吗？请你试着填一填。辐射图，有技巧。首位数，填中间，剩余成双面对面。辐射图，有技巧。末位数，填中间，剩余成双面对面。\n这类是辐射型数阵图，解题关键是找准中间数。中间数通常是一组有序数列中的首项、中间项或末项，再把剩下的数按照“大小配”分成几组，分别填入。\n练习：将3—9填入下图中，使每行3个数的和相等，有几种填法？\n例1、用1——7填入下图,使每行三个数的和相等。三组数都用到了最中间的数，那么每组都减去中间的那个数剩下的两个数的和相等12345671+7=2+6=3+54173526127744553366121322+7=3+6=4+51+6=2+5=3+4\n123456712345671234567\n练习：1.P16综12.P17能13.P16基1\n例2(补充)：将1—7填入图中,使每行三个数的和都是14\n“公用数”的求法：①先求出几个已知数的和②再求出所有行总和：每行的和×行数③求差：“所有行的总和—已知数的和”④差÷（行数—1）=中间数\n练习：1、将1—9填入图中，使每行的和都等于122、将1—11填入图中，使每行的和都等于183、将1—7填入图中，使每行的和都等于12第一题图第二题图第三题图\n例题3（书例2）：将1-9九个数字分别填在下图圆圈内，使三角形每条边上四个数的和是17.1+2+3+……+9=45每条边上的和是17，共有3条边那么总和是17×3=51.每个角上的数都被用了两次也就是每个角上的数都加了一次。51-45=66=1+2+317—1—2=1414=5＋917—1—3=1313=6＋717—2—3=1212=4＋8171717\n求角上几个数之和的方法：①先求出题中几个已知数的和②再求出所有行总和：每行之和×行数③求差：“所有行的总和—已知数的和”\n练习：1、将1—6填入三角形数阵图中，使每条边上的三个数的和等于102、P16基23、P17综24、P17能2（选做）\n（书例3）请把1—7添入下图，使每行三个数的和相等，并且圆上三个数的和也等于每行的和。例4621753463457212543167\n练习：2、请把1—13添入下图，使每边三个数的和相等，并且圆上五个数的和相等。（P16基3）1、请把1—7添入图中，使图中每个圆和每条直线上的三个数之和都相等。（P17能3）3、（选做）把1--8这八个自然数分别填入图中，使每个正方形四个角及每个对角线上四个数的和均是18。（P17综3）\n（书例4）把１－－７七个数分别填入下图，使每条线上三个数之和等于12例5先看竖着的三条线，有一个公用数12x3=36,1+2+3+4+5+6+7+8=2836-28=8,公用数用了两次8÷2=4每条线上和为12，所以另外两个数凑8.（1,7）（2,6）（3,5）根据横向和12调整41236574123657调整横向和12\n2、把1--8这八个数分别填入图内，使小正方形四个顶点之和等于大正方形四个顶点之和（综4）3、请你把1--8八个数分别填到下图中，使每个圆周上的数相加的和等于21。（能4）1、将1--6填入下图中，要求四条直线上的数之和都等于10。（基4）练习：\n不论是辐射型数阵阵、封闭型数还是复合型数阵解题的要点都是先确定公共部分的数。小结：\n七嘴八舌说说你的收获！数阵是由幻方演化出来的另一种数字图。一般按数的组合形式，将其分为三类，即辐射型数阵、封闭型数阵、复合型数阵下节课再见！