(2)向量的加减法 11页

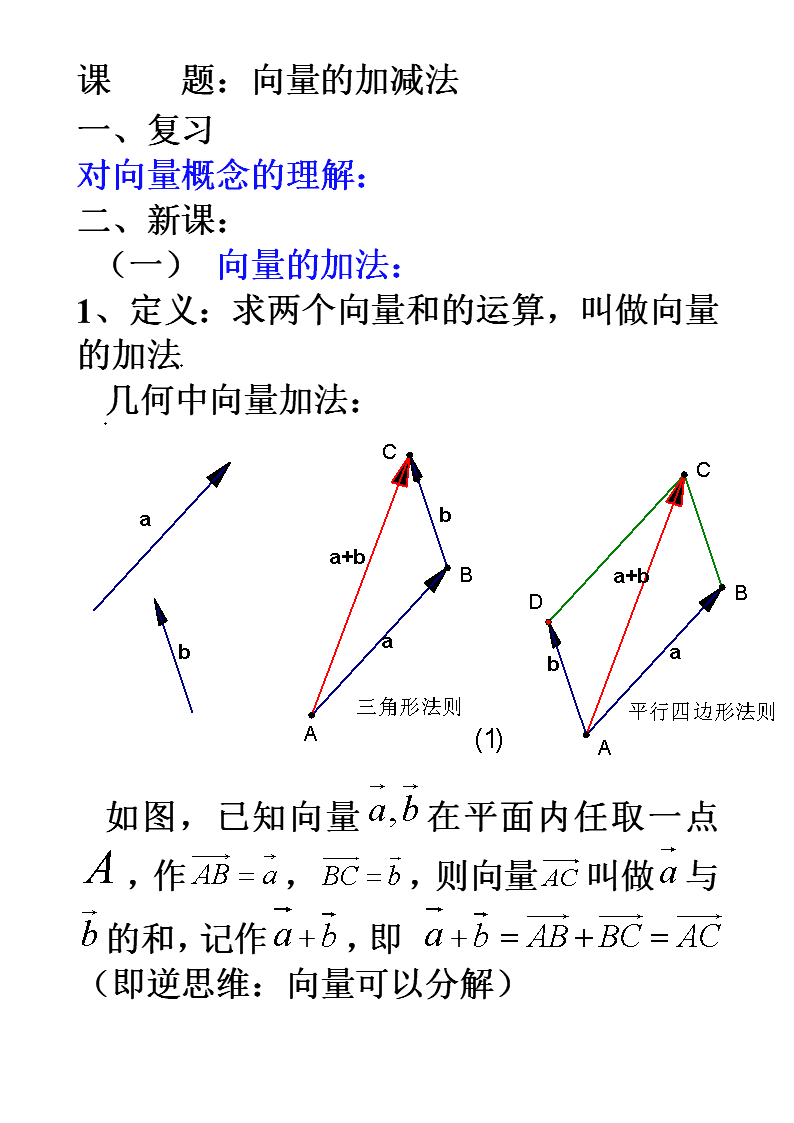
课题：向量的加减法一、复习对向量概念的理解：二、新课：（一）向量的加法：1、定义：求两个向量和的运算，叫做向量的加法几何中向量加法：如图，已知向量在平面内任取一点，作，，则向量叫做与的和，记作+，即+（即逆思维：向量可以分解）\n特殊情况：（1）（2）对于零向量与任一向量，有探究：（1）两向量的和仍是一个向量；（2）当向量与不共线时，+的方向不同向，且|+|||+||;（3）当与同向时，则+、、同向，且|+|||+||,\n当与反向时，若||>||,则+的方向与相同，且|+|=;若||<||,则+的方向与相同，且|+|=（4）“向量平移”（自由向量）：使前一个向量的终点为后一个向量的起点，可以推广到n个向量连加。封闭图形ABCDE中，一般有两种方法，（1）平行四边形法则（对于两个向量共线不适应）（2）三角形法则（“首尾相接，首尾连”）\n2．向量加法满足的运算律交换律：+=+结合律：(+)+=+(+)证：如图：使,,则(+)+=+(+)=∴(+)+=+(+)从而，多个向量的加法运算可以按照任意的次序、任意的组合来进行（二）向量的减法：1、定义：求两个向量差的运算叫做向量的减法减法的三角形法则作法：在平面内取一点\nO，作==,则=即可以表示为从向量的终点指向向量的终点的向量注意：1°表示强调：差向量“箭头”指向被减数2°加减统一，三、讲解范例：问题1：非零向量，应分别满足什么条件，下列等式（结论）成立①②③④\n⑤⑥⑦⑧之间的大小关系为；问题2：填空1、在正六边形ABCDEF中,,,则=.2、已知,,若||=12,||=5,且∠AOB=90°,则=.\n3、化简的结果是4、向量||=8,||=12,求|+|的最大值是，最小值是。5、已知与是非零向量,则时,应满足条件.6、在五边形ABCDE中,设,,,,用表示=.问题3：选择题1.下列等式:①②③④⑤\n正确的个数是(C)A.2B.3C.4D.52.下列等式中一定能成立的是(D)A.+=B.-=C.+=D.-=3.化简-++的结果等于(B) A.B.C.D.4、若O是内一点，且。则O是的（B）（A）垂心（B）重心（C）内心（D）外心五、小结1°向量加法的几何法则；2°交换律和结合律；\n3°向量减法的定义、作图法六、课后作业：1.在△ABC中,,,则等于()A.B.C.D.2.O为平行四边形ABCD平面上的点,设,，,,则AB.\nC.D.3.在下列各题中,正确的命题个数为()(1)若向量与方向相反,且,则与方向相同(2)若向量与方向相反,且,则与方向相同(3)若向量与方向相同,且,则与方向相反(4)若向量与方向相同,且,则与方向相反\nA.1B.2C.3D.44.如图，在四边形ABCD中,根据图示填空:，=,=,=,=.5.若与共线且成立,则与的关系为作业：练习册P85习题2A、B组