- 421.60 KB
- 2022-06-14 发布
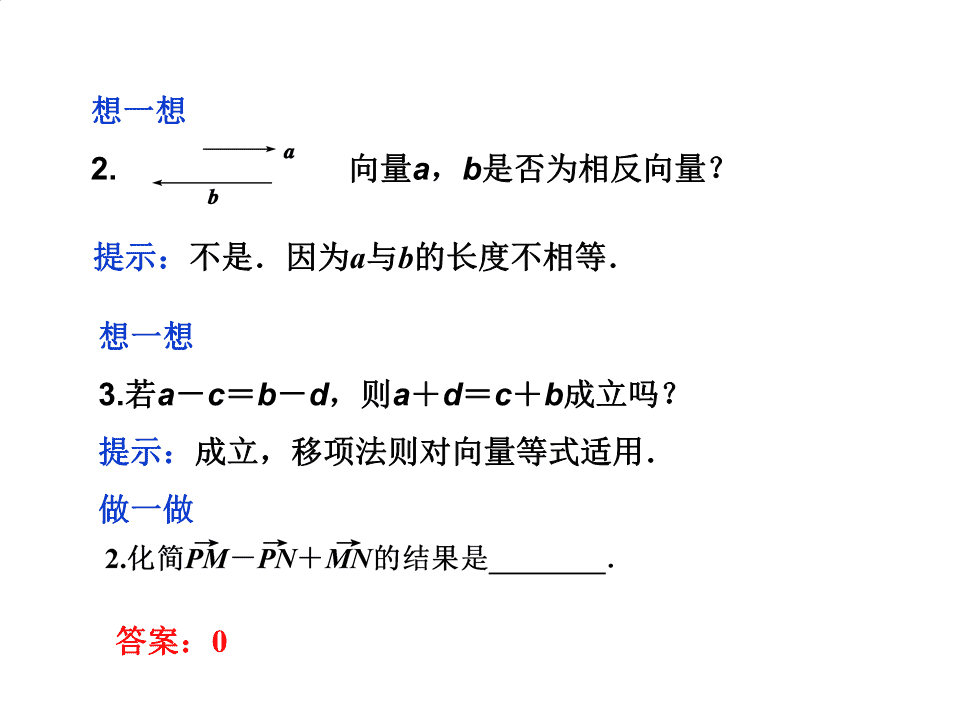
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第二章平面向量2.2平面向量的线性运算2.2.1向量加法运算及其几何意义2.2.2向量减法运算及其几何意义\n想一想1.两个向量相加就是两个向量的模相加吗?提示:不是.两个向量的和仍是一个向量,所以两个向量相加要注意两个方面,即和向量的方向和模.做一做\n想一想2.向量a,b是否为相反向量?提示:不是.因为a与b的长度不相等.想一想3.若a-c=b-d,则a+d=c+b成立吗?提示:成立,移项法则对向量等式适用.做一做答案:0\n题型一已知向量作和(差)向量例1如图所示,已知向量a,b,c,求作向量a+b-c.\n\n【点评】求两个向量的和向量时,要注意向量加法的三角形法则和平行四边形法则的应用.求两向量的差向量时,有以下两种思路:(1)可以转化为向量的加法来进行,如a-b,可以先作-b,然后用加法法则计算a+(-b)即可.(2)也可以直接用向量减法的三角形法则,即把两向量的起点重合,则差向量为连接两个向量的终点,指向被减向量的终点的向量.\n跟踪训练\n题型二向量的加减法运算例2\n【点评】进行向量的加减运算时,常用的变形如下:→→→→(1)运用AB=-BA或AB+BA=0化减为加.→→→(2)运用AB+BC=AC转化为“首尾顺次相接的形式相加”.→→→→→→(3)运用OA-OB=BA或AB=OB-OA转化为“同一点出发的两个\n跟踪训练\n题型三用已知向量表示其他向量例3\n\n【点评】解此类问题要根据图形的几何性质,运用向量的平行四边形法则和三角形法则解题.要特别注意向量的方向以及运算式中向量之间的关系.\n跟踪训练\n\no练习3:如图,已知向量ABa,ADb,DAB120,且|a||b|3,求|ab|和|ab|COD`B120obaA\n解:以AB、AD为邻边作平行四边形ABCD,由于|AD||AB|3,故此四边形为菱形由向量的加减法知CACab,DBabO故|AC||ab|,|DB||ab|D12`0oBbaOO因为DAB120,所以DAC60A所以ADC是正三角形,则|AC|3由于菱形对角线互相垂直平分,所以AOD是直角三角形,333o|OD||AD|sin60322所以|ab|3,|ab|33\n练习4.判断下列命题是否正确,若不正确,说明理由1、ABBA0()2、ABOAOB()3、相反向量就是方向相反的量()4、若ABBCCA0,则A、B、C三点是一个三角形的定点()5、0aa()6、两个向量是互为相反向量,则两个向量共线(√)\n练习5若AB8,AC5,则BC的取值范围是_____.解:BCACAB,ACABACABACAB3BC13