小学数学教案范文 8页

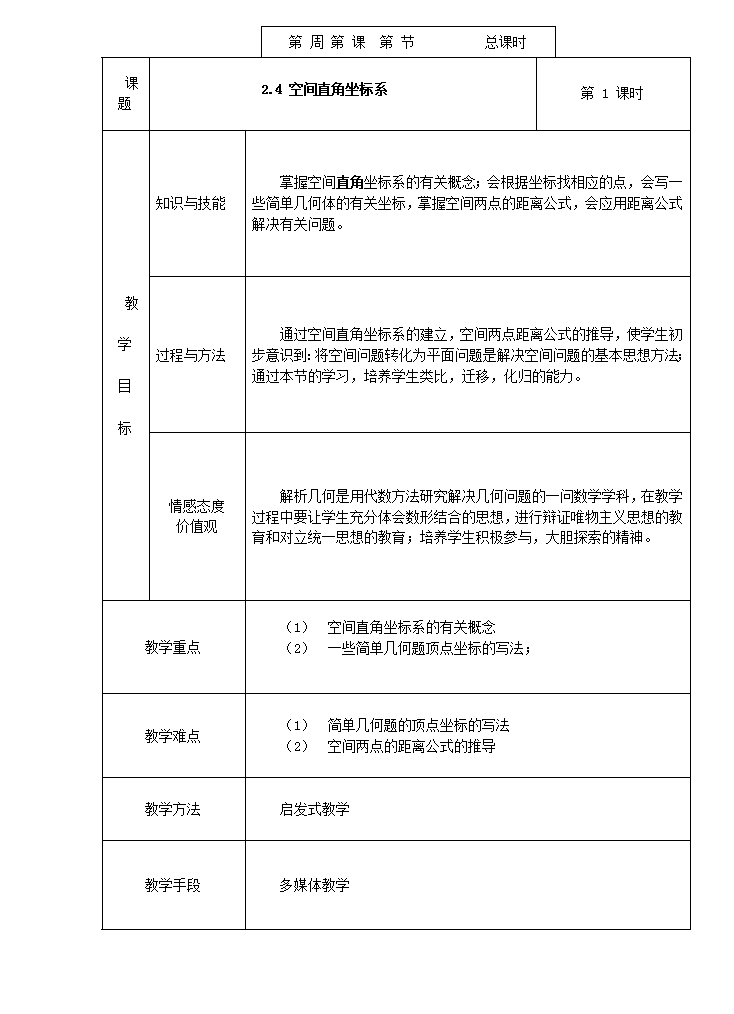
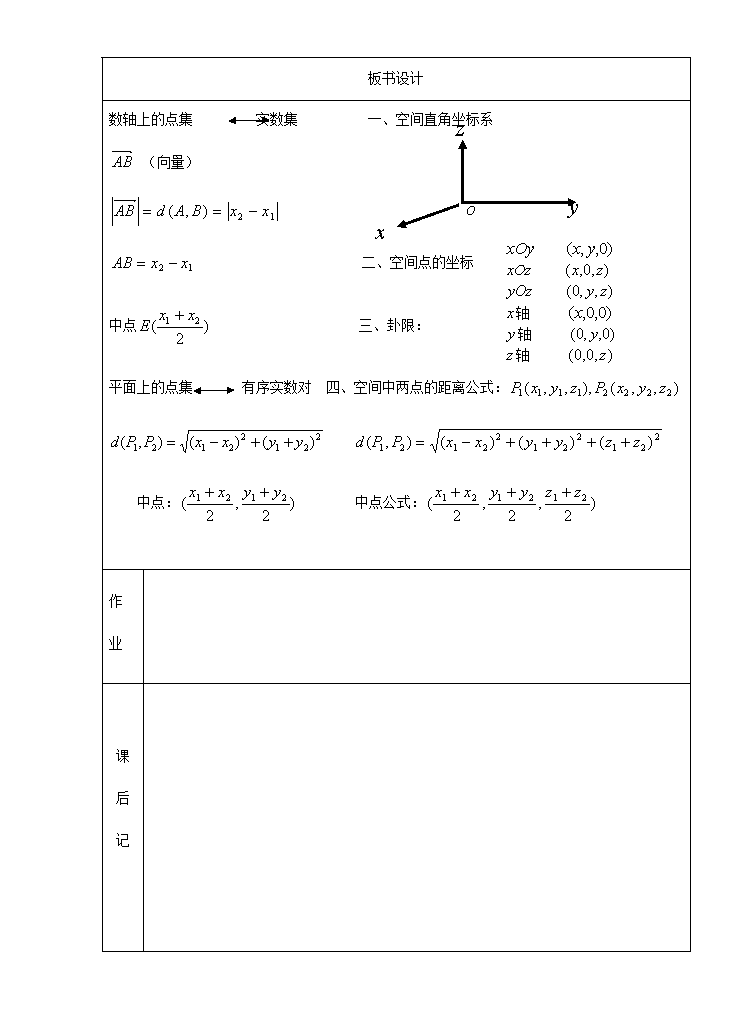
题课题第周第课第节总课时2.4空间直角坐标系第1课时教教学目标知识与技能掌握空间直角坐标系的有关概念；会根据坐标找相应的点，会写一些简单几何体的有关坐标，掌握空间两点的距离公式，会应用距离公式解决有关问题。过程与方法通过空间直角坐标系的建立，空间两点距离公式的推导，使学生初步意识到：将空间问题转化为平面问题是解决空间问题的基本思想方法；通过本节的学习，培养学生类比，迁移，化归的能力。情感态度价值观解析几何是用代数方法研究解决几何问题的一问数学学科，在教学过程中要让学生充分体会数形结合的思想，进行辩证唯物主义思想的教育和对立统一思想的教育；培养学生积极参与，大胆探索的精神。教学重点（1）空间直角坐标系的有关概念（2）一些简单几何题顶点坐标的写法；教学难点（1）简单几何题的顶点坐标的写法（2）空间两点的距离公式的推导教学方法启发式教学教学手段多媒体教学\n板书设计数轴上的点集实数集一、空间直角坐标系（向量）轴轴轴二、空间点的坐标中点三、卦限：平面上的点集有序实数对四、空间中两点的距离公式：中点：中点公式：作业课后记\n教学过程复习回顾：数轴：数轴上的点集实数集若数轴有两点：则：（向量）中点平面：平面上的点集有序实数对若点P与实数对对应，则叫做P点的坐标。其中，是如何确定的？平面内两点的距离公式：中点公式：则中点M的坐标为\n新课讲授：这节课我们研究空间直角坐标系。一、空间直角坐标系大家先来思考这样一个问题，天上的飞机，飞机的速度非常的快，即使民航飞机速度也非常快，有很多飞机时速都在1000km以上，而全世界又这么多，这些飞机在空中风驰电掣，速度是如此的快，岂不是很容易撞机吗？但事实上，飞机的失事率是极低的，比火车，汽车要低得多，原因是，飞机都是沿着国际统一划定的航线飞行，而在划定某条航线时，不仅要指出航线在地面上的经度和纬度，还要指出航线距离地面的高度。确定空间点的位置需要几个量？三个。为了确定空间点的位置，我们在直角坐标系中，通过原点，再作一条数轴，使它与轴，轴都垂直，这样它们中的任意两条互相垂直；轴的方向通常这样选择，从轴的正方向看，轴的正半轴沿逆时针方向转能与轴的正半轴重合，这时，我们说在空间建立了一个空间直角坐标系，叫做坐标原点。每两条坐标轴分别确定的平面，，，叫做坐标平面。二、空间点的坐标1、建立了空间直角坐标系后，空间内的任意一个点P也存在着一一对应关系，它和谁对应呢？平面内的点和两个实数构成的有序数对对应空间内的点和三个实数构成的有序数组对应若P与对应，则叫做P点的坐标。那是如何确定的呢？过P作一个平面平行于平面，（这样构成的平面同样垂直于轴），这个平面与\n轴交点记为，指的是轴上的坐标，这个数就叫做点P的坐标。过P作一个平面平行于平面，（这样构成的平面同样垂直于轴），这个平面与轴交点记为，指的是轴上的坐标，这个数就叫做点P的坐标。过P作一个平面平行于平面，（这样构成的平面同样垂直于轴），这个平面与轴交点记为，指的是轴上的坐标，这个数就叫做点P的坐标。这样我们对空间的一点，定义了由三个实数的有序数组作为它的坐标。那反过来，任意的三个实数的有序数组，是否能够确定空间的一个点P，与之对应呢？与刚刚的作图顺序恰好相反，在坐标轴上分别作出点，，，使它们在轴，轴，轴上的坐标分别是。再分别通过这些点这些平面平行于平面，，，这三个平面的交点，就是所求的点P.这样，在空间任意一点与三个实数的有序数组（点的坐标）之间，我们就建立起一一对应关系：P接下来，研究一下特殊点的坐标。平面（通过轴和轴的平面）是坐标形如的点构成的点集，其中，为任意的实数。平面（通过轴和轴的平面）是坐标形如的点构成的点集，其中，为任意的实数。平面（通过轴和轴的平面）是坐标形如的点构成的点集，其中，为任意的实数。\n轴是坐标形如的点构成的点集，其中为任意的实数。轴是坐标形如的点构成的点集，其中为任意的实数。轴是坐标形如的点构成的点集，其中为任意的实数。三、卦限：三个坐标平面把整个空间分成几部分呢？（8部分）每一部分称为一个卦限。①在坐标平面上方，分别对应坐标平面上四个象限的卦限，称为第Ⅰ、Ⅱ、Ⅲ、Ⅳ卦限，在下方的卦限称为第Ⅴ、Ⅵ、Ⅶ、Ⅷ卦限。分析：第Ⅰ、Ⅱ、Ⅲ、Ⅳ卦限分别对应坐标平面上方，且对应平面的第一、二、三、四象限，第Ⅴ卦限在第Ⅰ卦限的下方，依此类推。②点坐标各分量的符号第Ⅰ卦限：（+，+，+）等等。③注意：平面直角坐标系中，坐标轴上的点不在任何一个象限内，和它一样，空间直角坐标系中，坐标轴上的点和坐标平面上的点不属于任何卦限。④判断一个点位于第几卦限，可先判定落在平面的第几象限，再判断Z的符号，就可以判断点落的卦限。\nⅦ面面面ⅠⅡⅢⅣⅤⅥⅧ四、空间中两点的距离公式：特别的，当中点公式：则中点M的坐标为\n