- 499.81 KB
- 2022-06-17 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
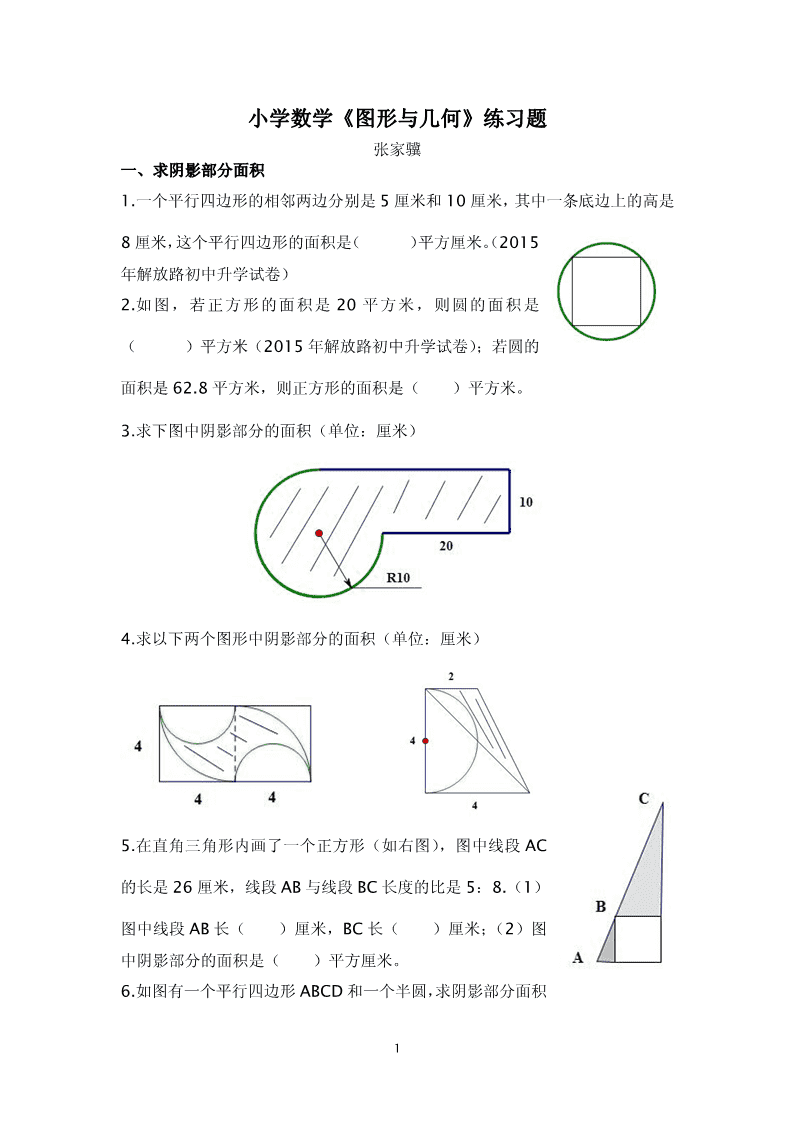
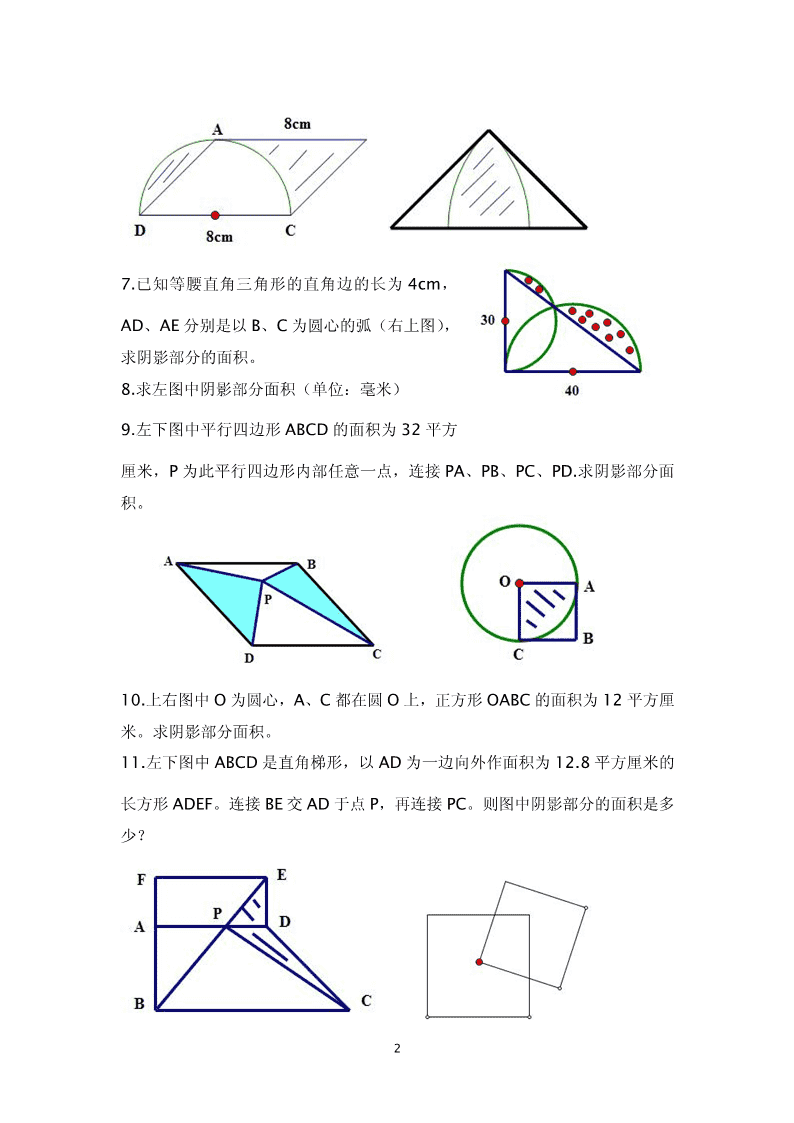
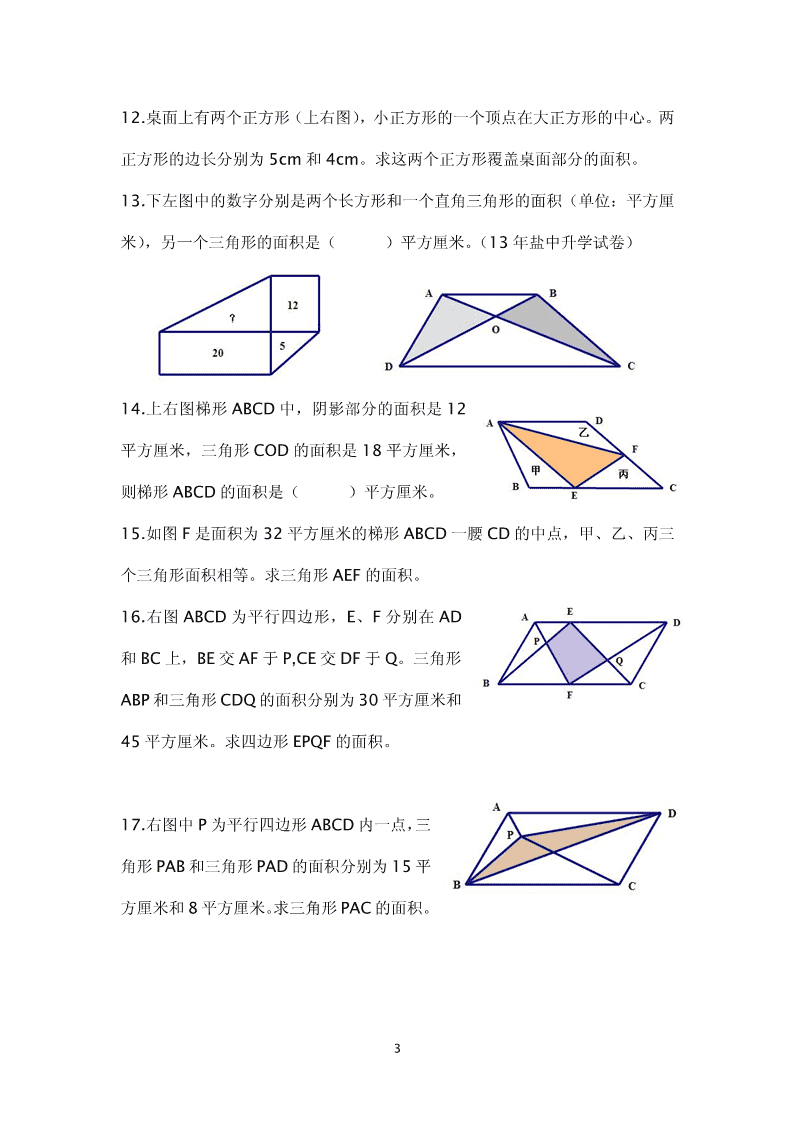
小学数学《图形与几何》练习题张家骥一、求阴影部分面积1.一个平行四边形的相邻两边分别是5厘米和10厘米,其中一条底边上的高是8厘米,这个平行四边形的面积是()平方厘米。(2015年解放路初中升学试卷)2.如图,若正方形的面积是20平方米,则圆的面积是()平方米(2015年解放路初中升学试卷);若圆的面积是62.8平方米,则正方形的面积是()平方米。3.求下图中阴影部分的面积(单位:厘米)4.求以下两个图形中阴影部分的面积(单位:厘米)5.在直角三角形内画了一个正方形(如右图),图中线段AC的长是26厘米,线段AB与线段BC长度的比是5:8.(1)图中线段AB长()厘米,BC长()厘米;(2)图中阴影部分的面积是()平方厘米。6.如图有一个平行四边形ABCD和一个半圆,求阴影部分面积。1\n7.已知等腰直角三角形的直角边的长为4cm,AD、AE分别是以B、C为圆心的弧(右上图),求阴影部分的面积。8.求左图中阴影部分面积(单位:毫米)9.左下图中平行四边形ABCD的面积为32平方厘米,P为此平行四边形内部任意一点,连接PA、PB、PC、PD.求阴影部分面积。10.上右图中O为圆心,A、C都在圆O上,正方形OABC的面积为12平方厘米。求阴影部分面积。11.左下图中ABCD是直角梯形,以AD为一边向外作面积为12.8平方厘米的长方形ADEF。连接BE交AD于点P,再连接PC。则图中阴影部分的面积是多少?2\n12.桌面上有两个正方形(上右图),小正方形的一个顶点在大正方形的中心。两正方形的边长分别为5cm和4cm。求这两个正方形覆盖桌面部分的面积。13.下左图中的数字分别是两个长方形和一个直角三角形的面积(单位:平方厘米),另一个三角形的面积是()平方厘米。(13年盐中升学试卷)14.上右图梯形ABCD中,阴影部分的面积是12平方厘米,三角形COD的面积是18平方厘米,则梯形ABCD的面积是()平方厘米。15.如图F是面积为32平方厘米的梯形ABCD一腰CD的中点,甲、乙、丙三个三角形面积相等。求三角形AEF的面积。16.右图ABCD为平行四边形,E、F分别在AD和BC上,BE交AF于P,CE交DF于Q。三角形ABP和三角形CDQ的面积分别为30平方厘米和45平方厘米。求四边形EPQF的面积。17.右图中P为平行四边形ABCD内一点,三角形PAB和三角形PAD的面积分别为15平方厘米和8平方厘米。求三角形PAC的面积。3\n求平面图形面积常用的几个方法1.直接求解。一般用于规则图形,直接用公式求解。2.分割法。将所求图形分割成几个图形逐个求解,再相加。3.求差或求补法。将所求图形看成几个图形的差。特别地,先求所求图形以外部分的面积,再用整个图形减去。4.移补法。将部分图形移补到另一人图形上,拼成一个简单图形求解。5.重叠法。将所求图形看成几个图形的重叠部分,然后用交集法求解。6.整体思维。将几个未知量或几个未知图形一起求解。7.等量替换。将某个图形换成另外一个与之面积相等的图形,然后再求。8.比例法。应用比和比例求未知量或未知图形。9.利用定式。利用典型图形和重要结论帮助分析求解。[练习]1.一个长方形,周长是32厘米,如果它的长和宽各增加3厘米,则面积将增加多少平方厘米?2.在长方形ABCD中,E是AB的中点,F是BC的中点。四边形ACFE的面积是24平方厘米。求长方形ABCD的面积。3.如图,平行四边形被分成分成甲、乙、丙三个三角形,甲的面积比乙的面积多4\n30平方厘米,乙的面积是丙的面积的1/3。这个平行四边形的面积是()平方厘米。(13年盐中分班试卷)4.如图两个正方形的边长分别为6cm和4cm,求阴影部分面积。求差求补5.求左下图中两个圆弧与边长为8cm的正方形的两个边长所围成的两个阴影部分的面积差。6.上右图中,在边长为6cm的正方形ABCD一边向外作一个正三角形ABE,连接ED交AB于F,连接AC,FC,求图中阴影部分面积。7.下左图中一个等腰直角三角形的直角边长为8cm,且正好等于一个半圆的直径,求阴影部分面积。8.上右图一个平行四边形的一条边为8cm,且正好等于半圆的直径,求阴影部5\n分面积。9.下左图有三段圆弧,中间是一个边长为6的正三角形,求阴影部分面积。10.上右图中有一个边长为1厘米的正方形和四个直径为1厘米的半圆。求阴影部分面积。11.上右图中三角形ABC的面积为36平方分米,AD=DC,AE=EF=FB。求阴影部分面积。12.有一块长20米,宽10米的长方形场地。如果在这块场地四周修筑2米宽的小路,中间植草皮。草地面积是多少平方米?小路的面积是多少平方米?13.下左图一个半径为4cm的四分之一圆内有两个半圆。求阴影部分面积。14.上右图是一个直角三角形,三边长分别为6cm,8cm,10cm。将最短边AB6\n折叠,使点B落在AC边上E点。求阴影部分面积。15.下左图将一个大长方形分成4个小长方形,其中三个长方形的面积分别为2,4,6(单位:平方厘米),求另一个长方形的面积。16.中上右图三角形ABC的边AB和AC上各取一点D和E,连接BE,CD交于F,三角形BCF和三角形CEF的面积分别等于8平方厘米和6平方厘米,F是CD的中点,求三角形ADE的面积。二、几何问题精选1.求下图中周长(单位:厘米)2.求下图立体图形的表面积7\n3.将一个注有水的瓶子先正放,后倒放(如下图)。求这只瓶子的容积。4.把一个直径为4厘米的圆柱体沿底面直径切开,分成若干等份,然后再拼成一个与它等底等高的近似长方体。这个长方体的表面积增加了40平方厘米。求这个长方体的体积。5.一个圆柱形玻璃杯内盛有水,水面高2.5厘米,玻璃杯内侧的底面积是72平方厘米。在这个杯中放进棱长是6厘米的正方体铁块后,水面没有淹没铁块。这时水面高多少厘米?6.把下面的正方体表面展开,得到的展开图是()7.近似于圆形的蚊香常用两盘合成,它的直径约是12厘米,使用时将它分开(如8\n图形态)。已知蚊香的宽度是0.6厘米,每小时燃烧15.7厘米。这样的一盘蚊香大约可以燃烧几小时?8.小聪用若干个1立方厘米的正方体摆成一个物体,下面是分别从正面、上面、左侧面看到的图形,这个物体的体积是多少立方厘米?9.有一个深4分米的长方体容器,其内侧是底面为边长3分米的正方形,当容器底面的一边紧贴桌面倾斜如右图时,容器内的水刚好不溢出。容器内的水有多少升?10.将一个长12厘米,宽5厘米的长方形圈成一个圆柱(无底),求这个圆柱的体积。11.一个底面半径为4分米,长为10分米的圆柱形木料,从左侧墙沿着直线滚到右侧墙正好滚了2周(如下图),那么两墙之间的距离是多少分米?12.把11块相同的长方体砖拼成一个大长方体。已知每块砖的体积是288立方厘米。则大长方体的表面积是多少平方厘米?13.先把一张正方形纸片对折,再沿着右图中的轨迹进行折叠,使A点恰好落在中线上。求角ABE的度数。9\n14.如图正方形ABCD的边长是8厘米,DEFG是一个长方形,宽DE=5厘米,求EF的长。15.实践操作:(1)图中每一个小正方形的边长为1厘米。请在图(1)中画一个正方形,使它的面积等于5平方厘米。(2)在图(2)的长方形中画一条线段,把它分成一个三角形和一个梯形,使得三角形和梯形的面积比为3:5(标明必要的数据或等份点。下同)(3)图(3)的长方形中画一条线段,把它分成两个直角梯形,其面积比为2:3.(4)图(4),过点M画一条线段,把它分成两个直角梯形,面积比为2:3.16.下面图形是用5个大小相同的正方形拼成,画一条直线,将它分成面积相等的两部分(设计三种不同的方案)(2015年盐中升学试卷)10\n[练习]1.用一根绳子捆扎一个长方体礼盒,如果结头处的绳子长30cm。求这根绳子的长度。2.在正方形ABCD中,边长是8厘米,又已知AE=10厘米,BF垂直于AE。求BF的长度。3.有一块草地,长36米,宽24米。有一个割草机宽40厘米,割草机推进的速度是每秒20厘米。问割完这块地需要多少时间?4.下左图中四边形ABCD、CDEF分别为长方形、平行四边形,阴影部分的面积是64平方厘米,BC=12厘米,CD=8厘米。AG的长应为多少厘米?5.上右图,正方形ABCD与三角形ABE重叠。已知乙的面积比甲大5平方厘米。a的长度是多少厘米?6.(1)把图(1)移到圆心在(6,8)的位置上。11\n(2)把图(2)长方形绕A点顺时针旋转90度。(3)画出图(3)轴对称图形的另一半。(2015年盐中升学试卷)7.实践操作:用几条线段,把边长为5厘米的正方形分割成面积相等的五个部分,要求:(1)用三种不同的方法;(2)每种方法的分割线条数不超过4条;(3)三种方法必须有一种是分割线长度总和最短的。8.一张正方形纸片,通过两次对折,然后按阴影部分进行裁剪并展开,可以得到下图来的“蝴蝶结”。请仿上图,将下面的正方形纸片经过两次对折后裁剪并展开,得到下图末的图形。请画出虚线和实线表示折叠过程,并用阴影表示剪去的部分。12