小学数学练习题中常见错误例谈 5页

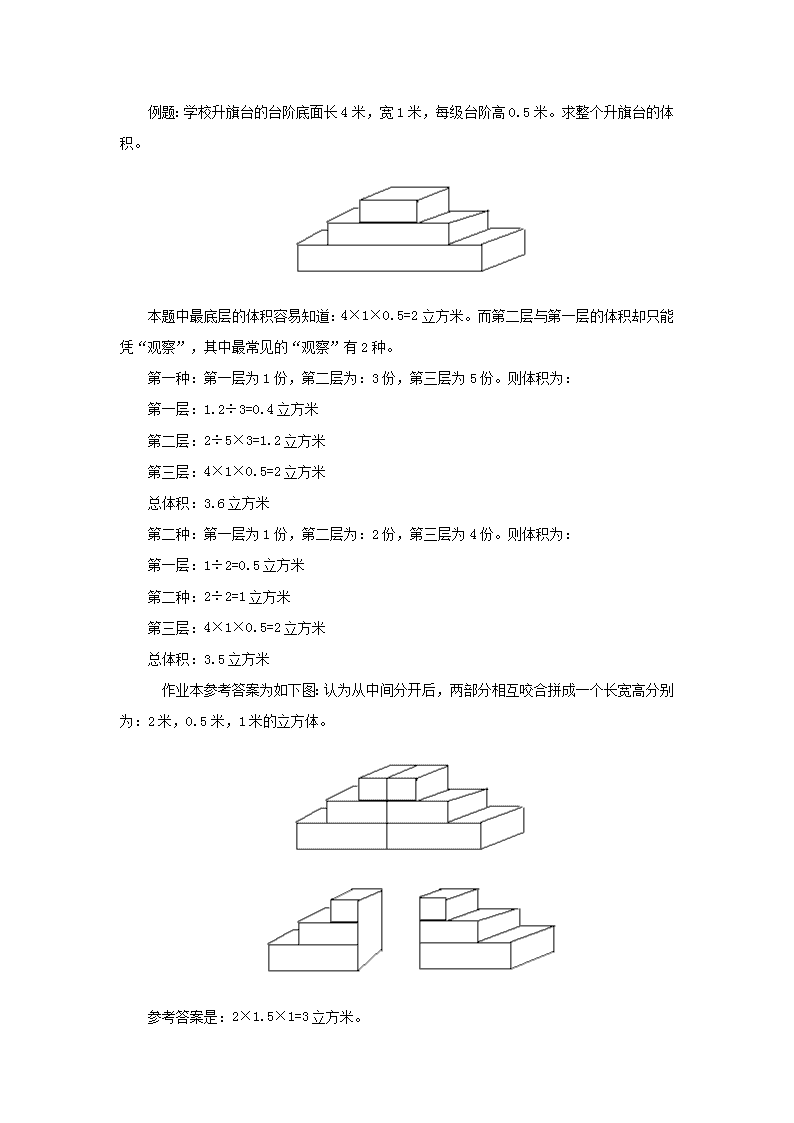
小学数学练习题中常见错误例谈桐乡市振兴西路小学胡志明在日常小学教学中我们经常会发现，相关配套作业本的练习题、参考答案等会存在种种错误。甚至于相关小学数学课本教材中存在问题的争论也屡见不鲜。只是，这些错误有的显而易见，有的如陷阱般深藏着。以下我通过三个例子浅析小学数学练习题中常见的错误。错误一：随心所欲、顾此失彼例题：新世纪小学图书馆1996年至2005年藏书量如下表。年份1996199719981999200020012002200320042005藏书量/万册22.533.54.55678101、你认为学校在哪一年投入的购书经费最多?为什么?2、2000年至2005年,学校共增加图书多少万册?3、你还能提出什么数学问题?　本题中存在的问题一：表格中是关注藏书的数量，而问题却是求经费的排名。很显然，要用册数来排名经费的话是有一定的误区的。也就是说册数越多并不一定就是经费最多。例如一本《汉语词典》的价格和平常的的杂志的价格那肯定可以是10倍的关系，甚至于可以更高的倍数关系。这样的话根据经费的计算（总价=单价*数量）这个问题的可能性就多了。存在的问题二：单讲册数多少的话，还存在着1996年和2005年购进图书册数相等的问题。存在的问题三：学生自己提出问题常常有人提出：2004年和2005年共藏书多少万册？学生列式：8+10=18（万册）粗一看全班几乎列式一致，应该问题不大。但是，这个2004年的册数是1996年到2004年的累计册数，事实上到2004年为止全部藏书就是8万册。到2005年止累计10万册，哪来的两年总数18册！这类问题的出现完全是命题者过于随心所欲，考虑了这里忘记了那里。学生在做的时候往往会“视而不见”的自动校正。作为老师对这些基本属于浅显性质的错误问题，自己更是要有清醒的认识。错误二：经验主义、忽略实践\n例题：学校升旗台的台阶底面长4米，宽1米，每级台阶高0.5米。求整个升旗台的体积。本题中最底层的体积容易知道：4×1×0.5=2立方米。而第二层与第一层的体积却只能凭“观察”，其中最常见的“观察”有2种。第一种：第一层为1份，第二层为：3份，第三层为5份。则体积为：第一层：1.2÷3=0.4立方米第二层：2÷5×3=1.2立方米第三层：4×1×0.5=2立方米总体积：3.6立方米第二种：第一层为1份，第二层为：2份，第三层为4份。则体积为：第一层：1÷2=0.5立方米第二种：2÷2=1立方米第三层：4×1×0.5=2立方米总体积：3.5立方米 作业本参考答案为如下图：认为从中间分开后，两部分相互咬合拼成一个长宽高分别为：2米，0.5米，1米的立方体。参考答案是：2×1.5×1=3立方米。\n 我了解到的学校老师有选择参考答案的。也有随学生发挥的。其实，由于题目的条件没有限制，所以上述出现的学生的两种“观察”（事实上应该叫做：猜测）都是对的。而且相比参考答案，学生的做法显然理由更加充分。因为仔细思考后不难发现，参考答案是有和学生猜测一样的假设而得到得，那么，参考答案到底把这三层的关系看做什么呢？由参考答案的长宽高分别为：2米，0.5米，1米的立方体，可以看出：参考答案把原来最底层的一半长，2米。作为拼组成的立方体的长宽没有变，高是0.5×3=1.5米。这里很明显的可以看出：拼组的时候，这个2米并没有和别的面相拼。因此，可以肯定原来的底层是作为独立层存在的，那么，第一层的一半肯定和第二层的一半相互拼组。而这样拼组的立方体显然高并不是0.5×3=1.5米，而应该是0.5×4=2米。这是参考答案的一个明显的错误。那么，参考答案还有可能是怎样假设的呢？再分析就知道只能是以下的假设：切开拼组时，左边第一层的一半和右边第三层拼组；第二层和第二层拼组，左边第三层的一半和右边第一层拼组。这样的拼组成的立方体(确切的应该先叫它组合体)，它的高是：0.5×3=1.5米，宽始终没有变，而它的长因该是2米加第一层的一半，所以超过2米。这里看来参考答案若是这样假设，又错误。其实，仔细考虑，这样的拼组其实，中间这层是碰不到的，应该有一个空洞（是立方体形状的）这个是很容易忽视的细节。计算长度可以发现这个问题，如果具体的剪下来做一做，很容易会发现这个问题。所以即使和参考答案一样的思路，也要考虑周全，不能近似的认为，都是阶梯状就一定能够相互咬合拼组。所以，考虑后得到：若是要如参考答案那样拼组。前提是：第一层和第二层的长度和正好是第三层长度的一半。这个题目之所以引起这样的分歧，主要是题目不够严谨，参考答案顾此失彼。这种题目老师通常会讲到图形的裁剪拼组方法，它的确是解决数学问题很常见的思想方法，但是再好的方法不加思考的乱用也会产生误导，总觉得不规则的图形可以拼组成规则的图形，忽略实践这一步，凭着想当然的冲劲分析问题，经验主义的固执解决问题，造成错误的结论。也是值得我们很好反思的。错误三：只见树木、不见森林例题：下图是某校的平面示意图，比例尺为1:5000，请借助刻度尺、量角器解答下列问题：1、以旗杆为原点，利用方向角和距离指出其余各点的具体位置。\n2、如果用（0，0）表示教师办公室的位置，且小正方形的边长为1个单位长度，水平向右和竖直向上取正值，你能写出其余各点的具体位置吗？本题中第一个问题，对于小学生来说由于知识局限，在方法上是没得选择的，他们只能用直尺、量角器量，最多就是认真度量减少差值，虽然理论上测量结果和计算结果应该一致，但是实践中往往得不到这样的如意结果，通常情况下相差一两度是很正常的。而且平时作业的要求中相关方位的测量也是允许这种误差的。这样放在小学阶段被视为正确的解法，用老师的眼光来看呢！很显然相对旗杆这个点，其余的各点都是与它处在特定的直角三角形中的，而且直角边长度都是可以一眼看出的。由于直角三角形的直角边有明确的数值，所以，很方便的就可以利用勾股定律求出斜边的长度；另一方面角度的问题也可以运用正弦函数等知识计算，再通过常用数表如正弦函数值查询表等可以查到精确到0.1度的角的值。所以，回过头再看让学生用通过测量得到的结果，简直就应该视为是错误了。如这里的教学楼的方位中，如果不是南偏西（或西偏南）45度，那就是明显错误了。而我认为出现这类问题等的根源是把这些点放置于标准的方格标尺中。作为老师在讲解这类问题的时候如果也停留在直尺、量角器的度量层次上，鼠目寸光给后继学习下结论，那出现的问题就不是误差了。\n教学类书籍中出现数学练习题中问题现象的存在本来也是很正常的，况且数学也是与时俱进不断发展的，现在正确的将来也不一定滴水不漏。关键是作为一线老师要有思考每个题目的耐心，我们把好自己的这一关，那么这类题目到达错误结果就多一道防线，就能尽可能严密的教给学生数学知识，少一些遗憾，踏踏实实送好学生小学这一程。