导学案.1探索勾股定理》导学案（自） 2页

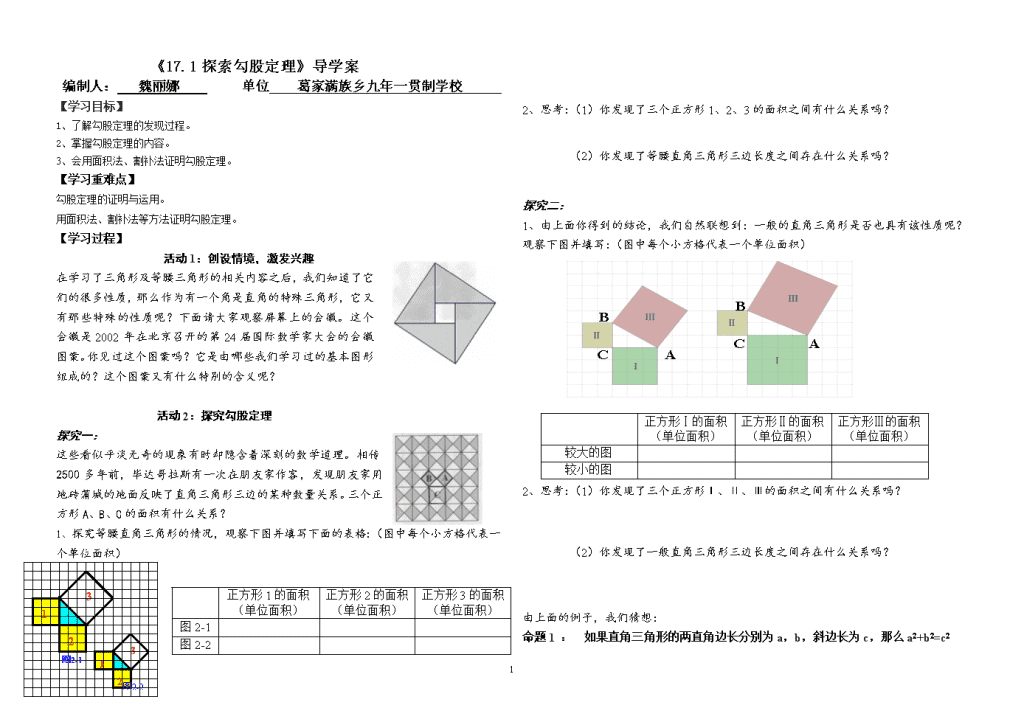
《17.1探索勾股定理》导学案编制人：魏丽娜单位葛家满族乡九年一贯制学校【学习目标】1、了解勾股定理的发现过程。2、掌握勾股定理的内容。3、会用面积法、割补法证明勾股定理。【学习重难点】勾股定理的证明与运用。用面积法、割补法等方法证明勾股定理。【学习过程】活动1：创设情境，激发兴趣在学习了三角形及等腰三角形的相关内容之后，我们知道了它们的很多性质，那么作为有一个角是直角的特殊三角形，它又有那些特殊的性质呢？下面请大家观察屏幕上的会徽。这个会徽是2002年在北京召开的第24届国际数学家大会的会徽图案。你见过这个图案吗？它是由哪些我们学习过的基本图形组成的？这个图案又有什么特别的含义呢？活动2：探究勾股定理探究一：这些看似平淡无奇的现象有时却隐含着深刻的数学道理。相传2500多年前，毕达哥拉斯有一次在朋友家作客，发现朋友家用地砖蒲城的地面反映了直角三角形三边的某种数量关系。三个正方形A、B、C的面积有什么关系？123123图2-1图2-21、探究等腰直角三角形的情况，观察下图并填写下面的表格：（图中每个小方格代表一个单位面积）正方形1的面积（单位面积）正方形2的面积（单位面积）正方形3的面积（单位面积）图2-1图2-22、思考：（1）你发现了三个正方形1、2、3的面积之间有什么关系吗？（2）你发现了等腰直角三角形三边长度之间存在什么关系吗？探究二：1、由上面你得到的结论，我们自然联想到：一般的直角三角形是否也具有该性质呢？观察下图并填写：（图中每个小方格代表一个单位面积）正方形Ⅰ的面积（单位面积）正方形Ⅱ的面积（单位面积）正方形Ⅲ的面积（单位面积）较大的图较小的图2、思考：（1）你发现了三个正方形Ⅰ、Ⅱ、Ⅲ的面积之间有什么关系吗？（2）你发现了一般直角三角形三边长度之间存在什么关系吗？由上面的例子，我们猜想：命题1：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2+b2=c22\ncab证一证1、拿出准备好的四个全等的直角三角形（设直角三角形的两条直角边分别为a，b，斜边c）；你能否就你拼出的图说明a²+b²=c²？2、你能用这四个直角三角形拼成一个正方形吗？拼一拼试试看。3、你拼的正方形中是否含有以斜边c的正形？（教师提示我们刚上课时见到的会徽图形）证明1：我国古人赵爽的证法，利用“赵爽弦图”证明.（图一）大正方形的面积可以表示为图一还可以表示为结论：当然证明的方法还有很多，同学们可以课后一起去讨论。（留作课后作业进行完成）大正方形的面积可以表示为图二还可以表示为结论：我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.因此就把命题1称为勾股定理.勾股定理如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2+b2=c2推理格式：∵△ABC为直角三角形∴AC2+BC2=AB2.（或a2+b2=c2）活动3：尝试应用，变式迁移例：如图，为得到池塘两岸A点和B点间的距离，观测者在C点设桩，使△ABC为直角三角形，并测得AC为100米，BC为80米.求A、B两点间的距离是多少？ABC练一练：1、判断正误:若直角三角形的两条边长为6cm、8cm，则第三边长一定为10cm.()68684658c2、小明的妈妈买了一部29英寸（约74厘米）的电视机。小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你同意他的想法吗？你能解释这是为什么吗？3、求下列直角三角形中未知边的长4、直角三角形的两直角边为5、12，则三角形的周长为。活动4：课堂小结课件展示：本课知识要点与检测，引导学生共同进行归纳小结。活动5：作业1、课本28页习题17.1的第2.3.4题。2、查询、探索勾股定理的其他证明方法。2