《函数》导学案 6页

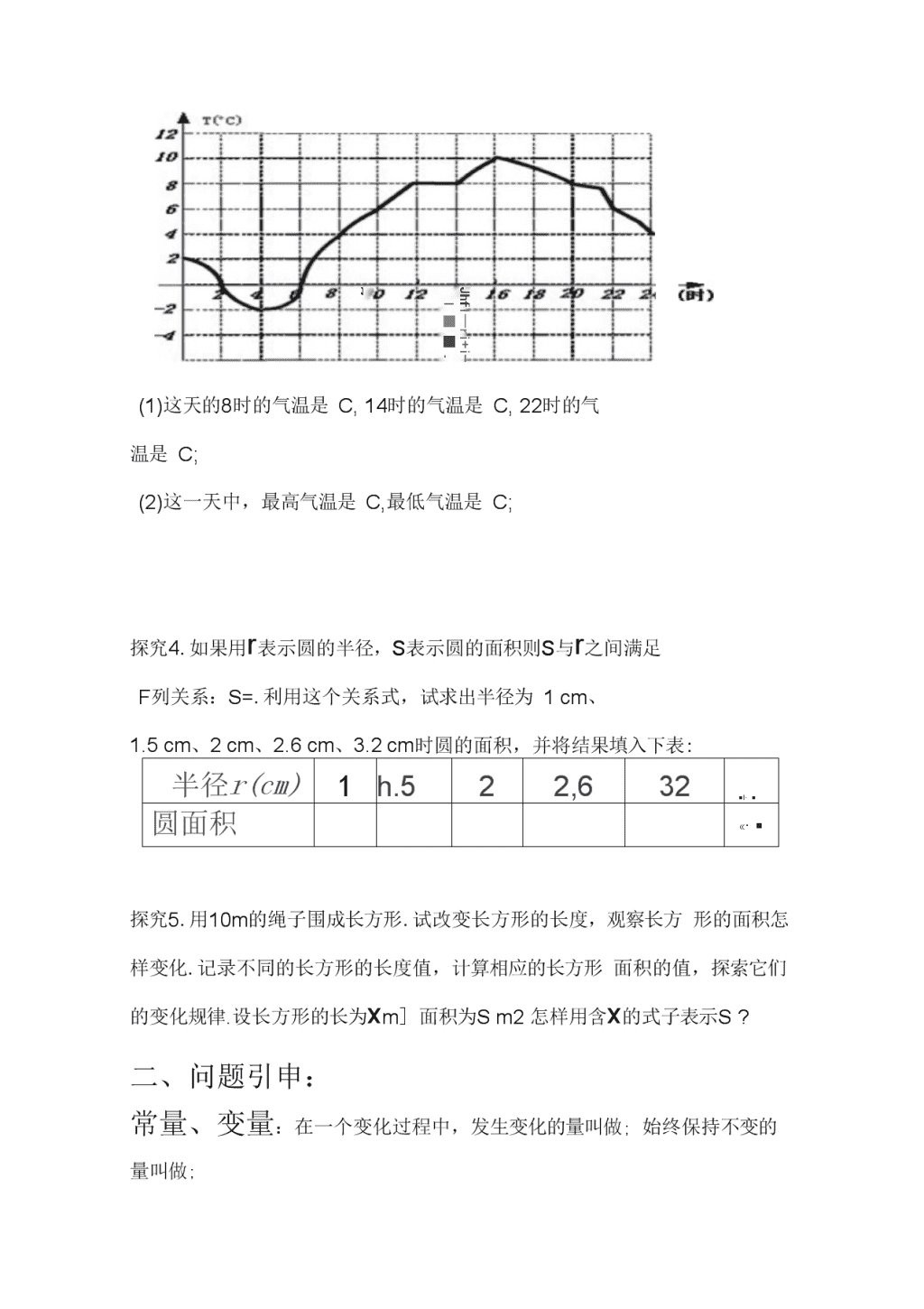
19.1函数学习目标1.理解解变量与常量的定义，能识别一个公式中或变化过程中的变量与常量2.理解函数的概念和三种表示方法，并能判断给定的两个量是否成函数关系学习过程：一：情境引入探究1.票房收入问题：每张电影票的售价为10元.（1）若一场售出150张电影票，则该场的票房收入是元；（2）若一场售出205张电影票，则该场的票房收入是元；（3）若设一场售出x张电影票，票房收入为y元，则y=。探究2.行程问题：汽车以60千米/小时的速度匀速行驶，行驶里程为s千米，行驶时间为t小时.请根据题意填表：t/时1234S/千米探究3.温度变化问题：如图是南通冬季某一天的气温T随时间t变化的图象，看图回\nzJhfl--ri+i-l■■.(1)这天的8时的气温是C,14时的气温是C,22时的气温是C;(2)这一天中，最高气温是C,最低气温是C;探究4.如果用r表示圆的半径，s表示圆的面积则s与r之间满足F列关系：S=.利用这个关系式，试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积，并将结果填入下表:半径r(cm)1h.522,632■I・■圆面积S(cm2)«・■探究5.用10m的绳子围成长方形.试改变长方形的长度，观察长方形的面积怎样变化.记录不同的长方形的长度值，计算相应的长方形面积的值，探索它们的变化规律.设长方形的长为xm］面积为Sm2怎样用含x的式子表示S?二、问题引申：常量、变量：在一个变化过程中，发生变化的量叫做;始终保持不变的量叫做;\n练习一：1.某位教师为学生购买数学辅导书，书的单价是4元，则总金额y（元）与学生数n（个）的关系式是,其中的变量是，常量是。2.计划购买50元的乒乓球，所能购买的总数n（个）与单价a（元）的关系式为，其中的变量是,常量3.圆的周长C与半径r的关系式为，这里的变量是,常量是。4.下列表格式是王辉从4岁到10岁的体重情况年龄（岁）,5678910…体重（千克）15.416.718；.019.621.523.225.2…这个问题中的变量是自变量、函数、函数值：1.“票房收入问题"中y=10x,有个变量，对于x的每一个值，y都有的值与之对应.\n1.“行程问题”中s=60t,有个变量，对于t的每一个值，s都有的值与之对应.2.“气温变化问题”，有个变量，对于时间t的每一个值，气温T都有的值与之对应.3.S表示圆的面积则S与r之间满足关系的关系式：有个变量，对于r的每一个值，s都有的值与之对应.5长方形的周长为10米，长为xm,面积为Sm2,有个变量，对于x的每一个值，s都有的值与之对应.归纳：函数的定义：如果在一个变化过程中有两个变量，对于x的每一个值，y都有的值与之对应，称x是,y是x的.例题：请看这些y是否是x函数？例题：看一个函数的图象如右图所示:1:y=X+12:y=2X2+3X—23:y2=X+14:|y|=X它表示的是函数吗?例题：一个三角形的底边为5,高h可以任意伸缩，三角形的面积也随之发生了变化.解：（1）面积s随高h变化的关系式s=,其中常量是,变量是,是自变量,是的函数；（2）当h=3时，面积s=,（3）当h=10时，面积s=;\n练习二1.购买一些签字笔，单价3元，总价为y元，签字笔为x支，根据题意填表：X（支）123…y（元）（1）y随x变化的关系式y=,是自变量，是的函数；（2）当购买8支签字笔时，总价为元.2.一个梯形的上底是4,下底是9,写出面积S随高h变化的函数关系式,常量是,变量是,自变量是,是的函数。3.小张准备将平时的零用钱节约一些储存起来.他已存有50元，从现在起每个月节存12元.设x个月后小张的存款数为y,试写出小张的存款数与从现在开始的月份数之间的函数关系式,其中常量是,变量是,自变量是,是的函数。思考题：填表并回答问题:x14916y2=x(1)对于x的每一个值，y都有唯一的值与之对应吗？答：。(2)y是x的函数吗？为什么？三、函数的不同表示法：回顾票房收入问题”、行程问题”、气温变化问题"表示两个变量的对应关系有哪些方法？\n(1)；(2)；(3).四、小结1.常量、变量、自变量、函数；2.辨析是否函数的关键：(1)是否存在变量，(2)是否符合唯一对应性；3.函数常见的表示方式：解析法、列表法、图象法。