小升初_数学_几何_专题 17页

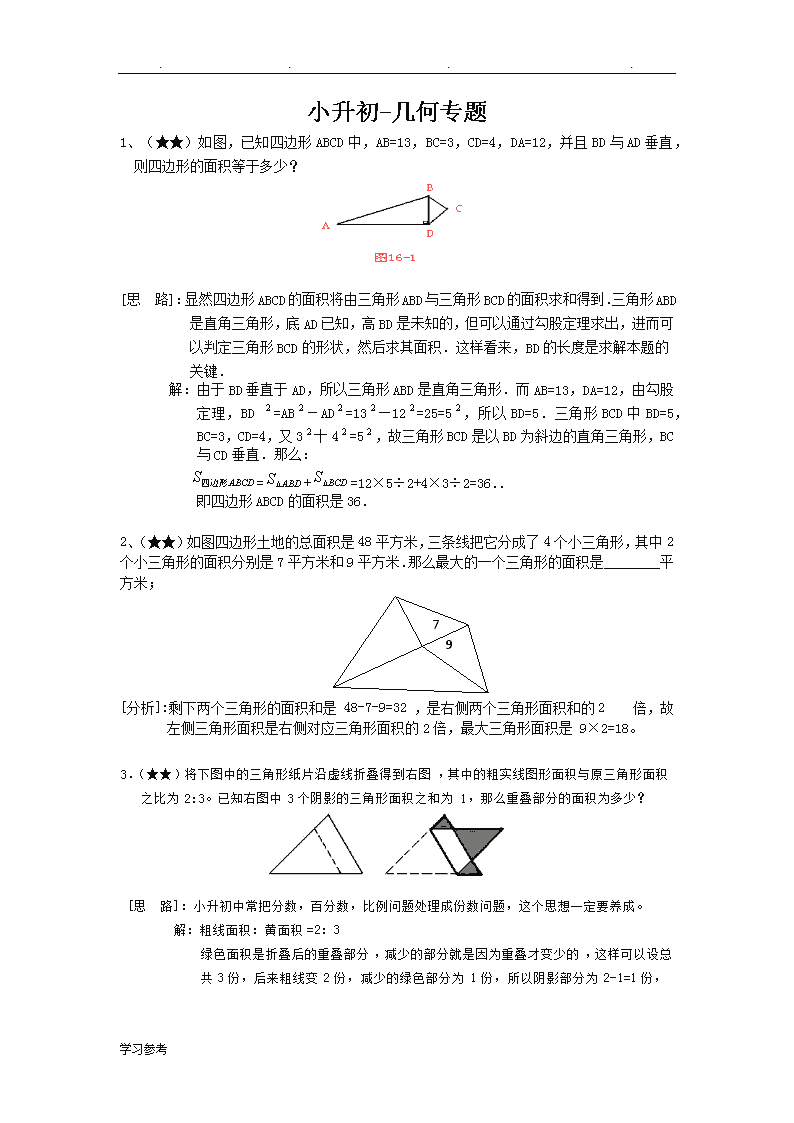
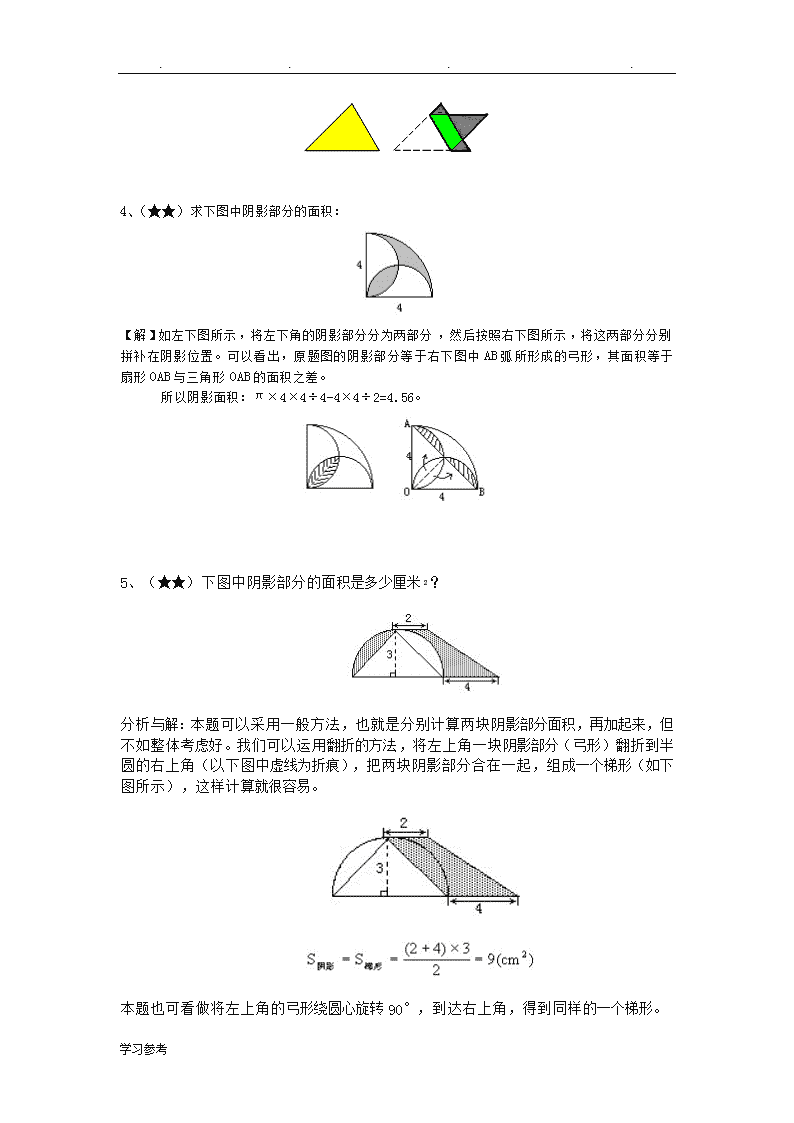
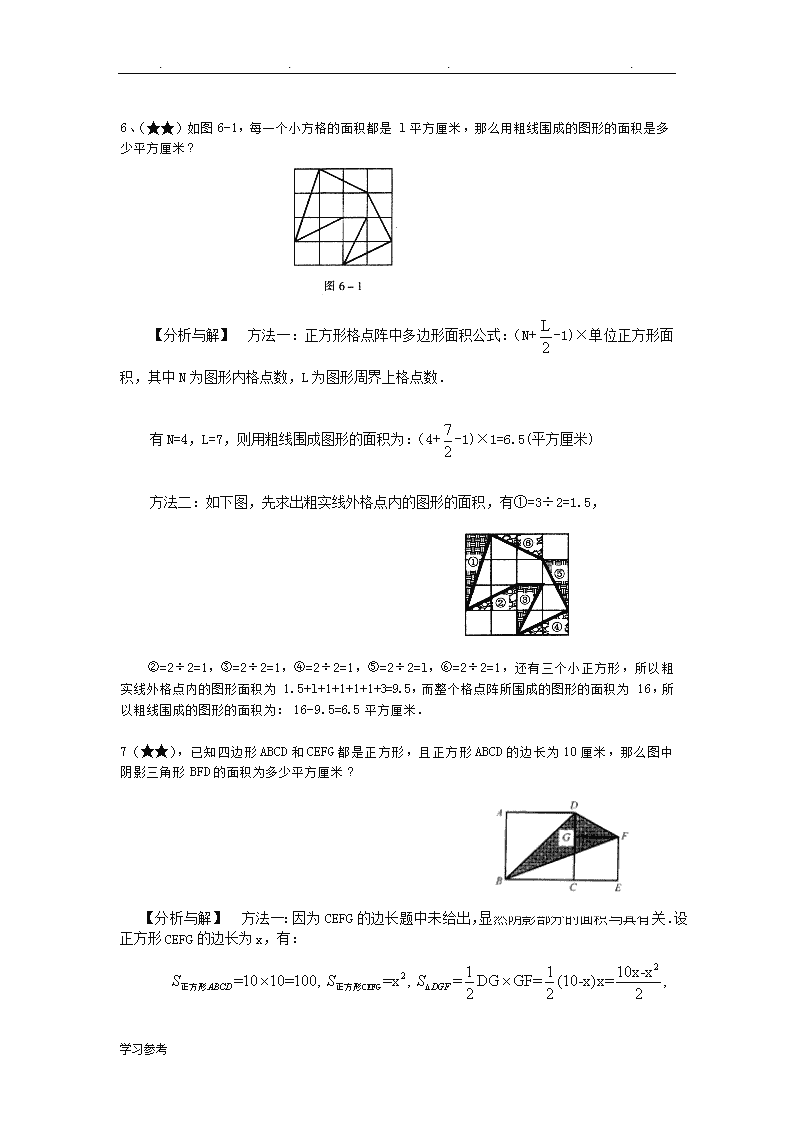
....小升初-几何专题1、（★★）如图，已知四边形ABCD中，AB=13，BC=3，CD=4，DA=12，并且BD与AD垂直，则四边形的面积等于多少？[思路]：显然四边形ABCD的面积将由三角形ABD与三角形BCD的面积求和得到．三角形ABD是直角三角形，底AD已知，高BD是未知的，但可以通过勾股定理求出，进而可以判定三角形BCD的形状，然后求其面积．这样看来，BD的长度是求解本题的关键．解：由于BD垂直于AD，所以三角形ABD是直角三角形．而AB=13，DA=12，由勾股定理，BD=AB－AD=13—12=25=5，所以BD=5．三角形BCD中BD=5，BC=3，CD=4，又3十4=5，故三角形BCD是以BD为斜边的直角三角形，BC与CD垂直．那么：=+=12×5÷2+4×3÷2=36．．即四边形ABCD的面积是36．2、（★★）如图四边形土地的总面积是48平方米，三条线把它分成了4个小三角形，其中2个小三角形的面积分别是7平方米和9平方米．那么最大的一个三角形的面积是________平方米；79[分析]:剩下两个三角形的面积和是48-7-9=32，是右侧两个三角形面积和的2倍，故左侧三角形面积是右侧对应三角形面积的2倍，最大三角形面积是9×2=18。3．（★★）将下图中的三角形纸片沿虚线折叠得到右图，其中的粗实线图形面积与原三角形面积之比为2:3。已知右图中3个阴影的三角形面积之和为1，那么重叠部分的面积为多少？[思路]：小升初中常把分数，百分数，比例问题处理成份数问题，这个思想一定要养成。解：粗线面积：黄面积=2：3绿色面积是折叠后的重叠部分，减少的部分就是因为重叠才变少的，这样可以设总共3份，后来粗线变2份，减少的绿色部分为1份，所以阴影部分为2-1=1份，学习参考\n....4、（★★）求下图中阴影部分的面积：【解】如左下图所示，将左下角的阴影部分分为两部分，然后按照右下图所示，将这两部分分别拼补在阴影位置。可以看出，原题图的阴影部分等于右下图中AB弧所形成的弓形，其面积等于扇形OAB与三角形OAB的面积之差。所以阴影面积：π×4×4÷4-4×4÷2=4.56。18,215、（★★）下图中阴影部分的面积是多少厘米2？分析与解：本题可以采用一般方法，也就是分别计算两块阴影部分面积，再加起来，但不如整体考虑好。我们可以运用翻折的方法，将左上角一块阴影部分（弓形）翻折到半圆的右上角（以下图中虚线为折痕），把两块阴影部分合在一起，组成一个梯形（如下图所示），这样计算就很容易。本题也可看做将左上角的弓形绕圆心旋转90°，到达右上角，得到同样的一个梯形。学习参考\n....6、（★★）如图6-1，每一个小方格的面积都是l平方厘米，那么用粗线围成的图形的面积是多少平方厘米?【分析与解】方法一：正方形格点阵中多边形面积公式：（N+-1)×单位正方形面积，其中N为图形内格点数，L为图形周界上格点数．有N=4，L=7，则用粗线围成图形的面积为：（4+-1)×1=6.5(平方厘米)方法二：如下图，先求出粗实线外格点内的图形的面积，有①=3÷2=1.5，②=2÷2=1，③=2÷2=1，④=2÷2=1，⑤=2÷2=l，⑥=2÷2=1，还有三个小正方形，所以粗实线外格点内的图形面积为1.5+l+1+1+1+1+3=9.5，而整个格点阵所围成的图形的面积为16，所以粗线围成的图形的面积为：16-9.5=6.5平方厘米．7（★★），已知四边形ABCD和CEFG都是正方形，且正方形ABCD的边长为10厘米，那么图中阴影三角形BFD的面积为多少平方厘米?【分析与解】方法一：因为CEFG的边长题中未给出，显然阴影部分的面积与其有关．设正方形CEFG的边长为x，有：学习参考\n....又阴影部分的面积为:(平方厘米).方法二：连接FC，有FC平行与DB，则四边形BCFD为梯形．有△DFB、△DBC共底DB，等高，所以这两个三角形的面积相等，显然,△DBC的面积(平方厘米)．阴影部分△DFB的面积为50平方厘米．8、（★★）用棱长是1厘米的正方块拼成如下图所示的立体图形，问该图形的表面积是多少平方厘米？[方法一]：[思路]：整体看待面积问题。解：不管叠多高，上下两面的表面积总是3×3；再看上下左右四个面，都是2×3+1，所以，总计9×2+7×4=18+28=46。[方法二]：[思路]：所有正方体表面积减去粘合的表面积解：从图中我们可以发现，总共有14个正方体，这样我们知道总共的表面积是：6×14=64，但总共粘合了18个面，这样就减少了18×1=18，所以剩下的表面积是64-18=46。[方法三]：直接数数。[思路]：通过图形，我们可以直接数出总共有46个面，每个面面积为1，这样总共的表面积就是46。9、（★★）一个圆柱形的玻璃杯中盛有水，水面高2.5cm，玻璃杯内侧的底面积是72cm2，在这个杯中放进棱长6cm的正方体铁块后，水面没有淹没铁块，这时水面高多少厘米？学习参考\n....　　解：水的体积为72×2.5=180（cm3），放入铁块后可以将水看做是底面积为72-6×6=32（cm2）的柱体，所以它的高为　　180÷32=5（cm）。10、（★★）有一个棱长为1米的立方体，沿长、宽、高分别切二刀、三刀、四刀后，成为60个小长方体(见左下图).这60个小长方体的表面积总和是______平方米.（06年三帆中学考试题）【解】原正方体表面积：1×1×6＝6（平方米），一共切了2＋3＋4＝9（次），每切一次增加2个面：2平方米。所以表面积：6＋2×9＝24（平方米）二：提高题11、（★★★）图是由正方形和半圆形组成的图形。其中P点为半圆周的中点，Q点为正方形一边的中点。已知正方形的边长为10，那么阴影部分面积是多少？（π取3.14.）[方法一]：阴影面积的“加减法”。[思路]：因为阴影部分面积不是正规图形，所以通过整个面积减去空白部分面积来求解。解：过P点向AB作垂线，这样空白部分面积分成上面的三角形和下面的梯形，这样阴影面积=整个面积-空白面积=（正方形ABCD+半圆）—（三角形+梯形）=（10×10+π×5×5÷2）-[15×5÷2+（5+15）×5÷2]=51.75[总结]：这种方法是小升初中最常用的方法，一定要学会这种处理思路。[方法二]：面积的“加减法”和“切割法”综合运用[思路]：出现正方形，出现弧线时，注意两个考点：1.半叶形2。1/4圆，所以我们可以先把面积补上再减去补上的面积解：S1=正方形-1/4圆=5×5-1/4×π×5×5学习参考\n....上面阴影面积=三角形APE-S1=15×5÷2-5×5-1/4×π×5×5下面阴影面积=三角形QPF-S2=所以阴影面积=（15×5÷2-5×5-1/4×π×5×5）+（10×5÷2-5×5-1/4×π×5×5）=51.75[方法三]：面积的“切割法”[思路]：出现正方形，出现弧线时，注意两个考点：1.半叶形2。1/4圆，这样可以考虑把阴影面积切成几个我们会算的规则图形解：半叶形S1=正方形-1/4圆=5×5-1/4×π×5×5上面阴影面积=三角形ADP+S1=10×5÷2+5×5—1/4×π×5×5下面阴影面积=三角形QPC+S2=5×5÷2+5×5—1/4×π×5×5阴影面积=（10×5÷2+5×5—1/4×π×5×5）+（5×5÷2+5×5—1/4×π×5×5）=51.7512、（★★★）如图，ABCG是4×7的长方形，DEFG是2×10的长方形，那么，三角形BCM的面积与三角形DCM的面积之差是多少？[方法一]：[思路]：公共部分的运用，这是小升初的常用方法，熟练找出公共部分是解题的关键。解:GC=7，GD=10推出HE=3；学习参考\n....BC=4，DE=2阴影BCM面积-阴影MDE面积=(BCM面积+空白面积)-(MDE面积+空白面积)=三角形BHE面积-长方形CDEH面积=3×6÷2-3×2=3[总结]：对于公共部分要大胆的进行处理,这样可以把原来无关的面积联系起来,达到解题的目的.[拓展]：如图,已知圆的直径为20,S1-S2=12,求BD的长度?[方法二]：[思路]：画阴影的两个三角形都是直角三角形，而BC和DE均为已知的，所以关键问题在于求CM和DM．这两条线段之和CD的长是易求的，所以只要知道它们的长度比就可以了，这恰好可以利用平行线BC与DE截成的比例线段求得．解:GC=7，GD=10知道CD=3；BC=4，DE=2知道BC:DE=CM:DM所以CM=2，MD=1。阴影面积差为:4×2÷2-1×2÷2=3[方法三]：连接BDS—S=S—S=(3×4—2×3)÷2=3．13．（★★★）如图所示，在三角形ABC中，DC＝3BD，DE＝EA。若三角形ABC的面积是1，则阴影部分的面积是多少？[方法一]：[思路]：阴影面积是两个不在一起的图形，我们先要通过等量代换，把两个图形拼成一个整体解：连接FD，因为AE=DE，所以S1=S3，S2=S4，S1+S2=S3+S4，即三角形AFC=三角形FCD，阴影面积等于S3+S4的面积。又因为DC＝3BD，三角形FDC=3×三角形BDF，这样我们就可以设三角形DFB为1份，则三角形FDC=3份，三角形AFC=三角形FCD=3份，这样总共面积分成7份，学习参考\n....所以阴影面积为1÷7×3=3/7[方法一]：14、（★★★）如图，在△ABC中，AD是AC的三分之一，AE是AB的四分之一，若△AED的面积是2平方厘米，那么△ABC的面积是多大？[分析]连结EC，如图，因为AC＝3AD，△AED与△AEC中AD，AC边上的高相同，所以△AEC的面积是△AED面积的3倍，即△AEC面积是6平方厘米，用同样方法可判断△ABC的面积且△AEC面积的四倍，所以△ABC的面积是6×4＝24（平方厘米）。15（★★★）从一块正方形木板锯下宽为米的一个木条以后，剩下的面积是平方米．问锯下的木条面积是多少平方米?【分析与解】我们画出示意图(a)，则剩下的木块为图(b)，将4块剩下的木块如下拼成一个正方形得到图(c)．学习参考\n....我们称AB为长，AD为宽，有长与宽的差为，所以图(c)中心的小正方形边长为，于是大正方形AEHK的面积为×4+×==×，所以AK长为．即，长+宽=，已知：长-宽=，得长=，于是锯去部分的木条的面积为×==1(平方米)．16、（★★★）将三角形ABC的BA边延长1倍到D；CB边延长2倍到E，AC边延长3倍到F，如果三角形ABC的面积等于1，那么三角形DEF的面积是_____。[分析]如图，连接CD、BF，则三角形ADC的面积＝三角形ABC的面积＝1；三角形BDE的面积＝三角形BCD的面积×2＝(1+1)×2＝4；三角形CDF的面积＝三角形ADC的面积×3＝3；三角形BCF的面积＝三角形ABC的面积×3＝3；三角形BEF的面积＝三角形BCF的面积×2＝6；三角形DEF的面积＝三角形ABC的面积+三角形ADC的面积+三角形BDE的面积+三角形CDF的面积+三角形BCF的面积+三角形BEF的面积＝1+1+4+3+3+6＝18。17、（★★★）如图，已知AE＝AC/5，CD＝BC/4，BF＝AB/6，那么等于多少？学习参考\n....[分析]这道题与例34很相像，但不同的是没有一个现成的单位面积。要求出这样一个比例，要求我们自己开发一个单位面积。可不可以就用大三角形的面积做单位面积呢？如图，连接AD，那么S△CDE＝S△ACD×4/5＝S△ABC×1/4×4/5＝S△ABC×1/5同理，连接BE，那么S△AEF＝S△ABE×5/6＝S△ABC×1/5×5/6＝S△ABC×1/6连接CF，那么S△BDF＝S△BCF×3/4＝S△ABC×1/6×3/4＝S△ABC×1/8所以＝1－1/5－1/6－1/8＝18、（★★★）如图，已知D是BC中点，E是CD中点，F是AC中点。三角形ABC由①~⑥这6部分组成，其中②比⑤多6平方厘米。那么三角形ABC的面积是多少？[分析]仔细观察图形，我们可以发现②和⑤这两个三角形形状是一样的，并且EF是△ACD的中位线，也就是EF：AD＝1：2。那么②和⑤底和高的比都是2：1（形状相同，高之比和底之比是一样的），面积比自然就是4：1了。②与⑤的面积比为4：1，并且相差6平方厘米，所以⑤的面积＝6÷（4－1）＝2（平方厘米）学习参考\n....②的面积＝2×4＝8（平方厘米）③与④的面积均为⑤的二倍，②的一半，即4平方厘米；⑥的面积为④＋⑤，即4＋2＝6（平方厘米）①的面积为②＋③＋④＋⑤＋⑥，即8＋4＋4＋2＋6＝24（平方厘米）大三角形的面积为①的二倍，即24×2＝48（平方厘米）。19、（★★★）在ΔABC中BD：DC=2:1,AE：EC=1:3求BO：OE。OABDCE[分析]:解法一，用按比例分配的方法，观察线段BE正好被AD分成BO与OE两部分，求这两部分的比，可以AD为底，B，E为顶点构造两个三角形，BAD与EAD，这样就可以面积比与线段比之间架一座桥。因为三角形BAD的三个顶点都在三角形ABC的边上，因此把三角形ABC的面积看作单位“1”，就可以用来表示ABD的面积，用AE的长占AC的1/4，CD的长占CB的1/3，=来表示AED的面积。因为：SΔABD：SΔAED=：=8：1，所以BO：OE=8：1。解法二：这幅图形一看就感觉它是燕尾定理的基本图，但2个燕尾似乎少了一个，因此应该补全，所以第一步我们要连接OC，因为AE:EC=1:3(条件)所以SΔAOE/SΔCOE=1:3若设SΔAOE=x,则SΔCOE=3xSΔAOC=4x,根据燕尾定理SΔAOB：SΔAOC=BD：DC=2:1所以SΔAOB=8xBO：OE=SΔAOB：SΔAOE=8x：x=8:1。20、（★★★）角形ABC中，C是直角，已知AC＝2，CD＝2,CB=3,AM=BM，那么三角形AMN（阴影部分）的面积是多少？学习参考\n....[分析]:可以连接NB，由燕尾定理及条件可知CAN：ABN＝2：1，不妨设ANM为1份，则ANB为两份，CAN就是4份，CND也是4份，全图就是10份，阴影就占全图的21（★★★）在图中，直线CF与平行四边形ABCD的AB边相交于E点，如果三角形BEF的面积为6平方厘米，求三角形ADE的面积是多少？[分析]:连结AC，因为AB平得CD，AE是三角形ADE，ACE的公共底边，所以三角形ADE与三角形ACE的面积相等。又因为BC平行于AF，AF是三角形AFC与三角形ABF的公共底边，所以三角形ACF与三角形ABF的面积相等。从图中还可看出，三角形ACF的面积＝三角形ACE的面积+三角形AEF的面积，三角形ABF的面积＝三角形BEF的面积+三角形AEF的面积。从上面两个等式可以得到三角形ACE的面积＝三角形BEF的面积，而三角形BEF的面积为6平方厘米，所以三角形ACE的面积也为6平方厘米，再根据三角形ADE与三角形ACE的面积相等可得三角形ADE的面积为6平方厘米。所以三角形ADE的面积为6平方厘米。22、（★★★）图中的四边形土地总面积为52公顷，两条对角线把它分成了4个小三角形，其中2个小三角形的面积分别是6公顷和7公顷。那么最大的一个三角形的面积是多少公顷？[分析]:我们不妨把四个小三角形看成四个元素，而不是整体的一部分。如图，四个小三角形面积中，两个是我们已知的，另两个未知。已知的两个三角形有共同的底边，所以它们的高之比就等于面积比6：7；S1与S2同样有共同的底边，并且它们的高分别与面积为6和7的两个小三角形相同，也就是同样有6：7的关系。这样S1：S2＝6：7；这样，原来的问题就变成一个和倍问题了。很容易知道S1＝(52－6－7)÷(6＋7)×6＝18（公顷）S2＝(52－6－7)÷(6＋7)×7＝21（公顷）学习参考\n....这样四个三角形的面积分别为6、7、18、21，最大的一个为21。23、（★★★）如图，在三角形ABC中，，D为BC的中点，E为AB上的一点，且BE=AB,已知四边形EDCA的面积是35，求三角形ABC的面积.（06年清华附中入学测试题）【解】根据定理：==，所以四边形ACDE的面积就是6-1=5份，这样三角形35÷5×6=42。24、（★★★）四个完全一样的直角三角形和一个小正方形拼成一个大正方(如图)如果小正方形面积是1平方米，大正方形面积是5平方米，那麽直角三角形中，最短的直角边长度是______米.（06年实验中学入学测试题）【解】小正方形面积是1平方米，大正方形面积是5平方米，所以外边四个面积和是5-1=4，所以每个三角形的面积是1，这个图形是“玄形”，所以长直角边和短直角边差就是中间正方形的边长，所以求出短边长就是1。25、（★★★）如图在长方形ABCD中，△ABE、△ADF、四边形AECF的面积相等。△AEF的面积是长方形ABCD面积的______(填几分之几)。（03年资源杯试题）。【解】连接AC，首先学习参考\n....△ABC和△ADC的面积相等，又△ABE和△ADF的面积相等，则△AEC和△AFC的面积也相等且等于ABCD的1/6，不难得△AEC与△ABE的面积之比为1/2，由于这两个三角形同高，则EC与BE之比为1/2，同理FC与DF之比也为1/2。从而△ECF相当于ABCD面积的1/18，而四边形AECF相当于ABCD面积的1/3，从而答案为1/3-1/18=5/18。26、（★★★）如图1，一个长方形被切成8块，其中三块的面积分别为12，23，32，则图中阴影部分的面积为_____（01年同方杯）【解】设图示两个三角形的面积分别为a和b，因为△AED面积等于ABCD的一半，则△ABE加上△DEC的面积也等于ABCD的一半。而△FDC的面积也等于ABCD的一半，即23+a+32+12+b=a+b+阴影面积，可见阴影面积=23+32+12=67。27、（★★★）右图中AB=3厘米，CD=12厘米，ED=8厘米，AF=7厘米.四边形ABDE的面积是平方厘米．【解】：四边形AFDC的面积=三角形AFD+三角形ADC=（×FD×AF）+（×AC×CD）=（FE+ED）×AF+（AB+BC）×CD=（×FE×AF+×ED×AF）+（×AB×CD+×BC×CD）。所以阴影面积=四边形AFDC-三角形AFE—三角形BCD=（×FE×AF+×ED×AF）+（×AB×CD+×BC×CD）-×FE×AF-×BC×CD=×ED×AF+×AB×CD=×8×7+×3×12=28+18=46。学习参考\n....28、（★★★）如图，三个一样大小的正方形放在一个长方形的盒内，A和B是两个正方形重叠部分，C，D，E是空出的部分，这些部分都是长方形，其中4个的面积比是A:B:C:D＝1:2:3:4。那么这个长方形的长与宽之比是多少？：[方法]：29．（★★★）如图，长方形的面积是小于100的整数，它的内部有三个边长是整数的正方形，①号正方形的边长是长方形长的5/12，②号正方形的边长是长方形宽的1/8。那么，图中阴影部分的面积是多少？[方法一]：从整除入手，我们可以推出长方形的面积只能是8×12=96，再入手就很简单可。解：①的面积就是5×5=25②的面积是1×1=1最大的空白正方形面积=（8-1）×（8-1）=49阴影面积=96-49-25-1=2130、（★★★）图30-10是一个正方形，其中所标数值的单位是厘米．问：阴影部分的面积是多少平方厘米?学习参考\n....【分析与解】如下图所示，为了方便所叙，将某些点标上字母，并连接BG．设△AEG的面积为x，显然△EBG、△BFG、△FCG的面积均为x，则△ABF的面积为3x，即，那么正方形内空白部分的面积为.所以原题中阴影部分面积为(平方厘米)．【挑战题】1、（★★★★）一块三角形草坪前，工人王师傅正在用剪草机剪草坪．一看到小灵通，王师傅热情地招呼，说：“小灵通，听说你很会动脑筋，我也想问问你，这块草坪我把它分成东、西、南、北四部分(如图)．修剪西部、东部、南部各需10分钟，16分钟，20分钟．请你想一想修剪北部需要多少分钟？（05年101中学入学测试题）【解】如下所示：将北部分成两个三角形，并标上字母那么有，即有，解得．所以修剪北部草坪需要20+24＝44分钟．评注：在本题中使用到了比例关系，即：S△ABG：S△AGC＝S△AGE：S△GEC＝BE：EC；学习参考\n....S△BGA：S△BGC＝S△AGF：S△GFC＝AF：FC；S△AGC：S△BCG＝S△ADG：S△DGB＝AD：DB；2、（★★★★）如图，正方形ABCD的面积是120平方厘米，E是AB的中点，F是BC的中点，四边形BGHF的面积是________平方厘米。解：[方法一]：通过比列求解解：延长EB到K，使BK=CD。三角形EGK与三角形DGC成比例，DC：EK=2：3，所以DG：GK=2：3，由于三角形DEK=90，所以EGK=90÷3/5=54，所以四边形EBFG=EGK-BKF=24。同理，EB：DC=1：2，所以BH：HC=1：2，所以三角形EBH=1/3EBD=10所以，四边形BGHF的面积是24-10=14[方法二]：份数解：120÷5=24(平方厘米)  可将该正方形的面积平均分成5份,每份为24(平方厘米)  120÷4=30(平方厘米)  是S△EBC=30(平方厘米)，所以  S△HFC=30-24=6(平方厘米)  在△EBG和△CDG中  EB:CD=1:2(底的比) ;高的比也是1:2 所以  S△EBG:S△CDG=1:4设正方形的边长为"1"， 所以  S△CDG=1×(2/3)÷2=1/3而正方形的面积为"1"  是120平方厘米， 所以  S△CDG=120×(1/3)=40(平方厘米)   S△DBC=120÷2=60(平方厘米)    S四边形BGHF=S△DBC-S△DCG-S△HFC                  =60--40-6                  =20-6                  =14(平方厘米)宁可累死在路上，也不能闲死在家里！宁可去碰壁，也不能面壁。是狼就要练好牙，是羊就要练好腿。什么是奋斗？奋斗就是每天很难，可一年一年却越来越容易。不奋斗就是每天都很容易，可一年一年越来越难。能干的人，不在情绪上计较，只在做事上认真；无能的人！不在做事上认真，只在情绪上计较。拼一个春夏秋冬！赢一个无悔人生！早安！—————献给所有努力的人.学习参考