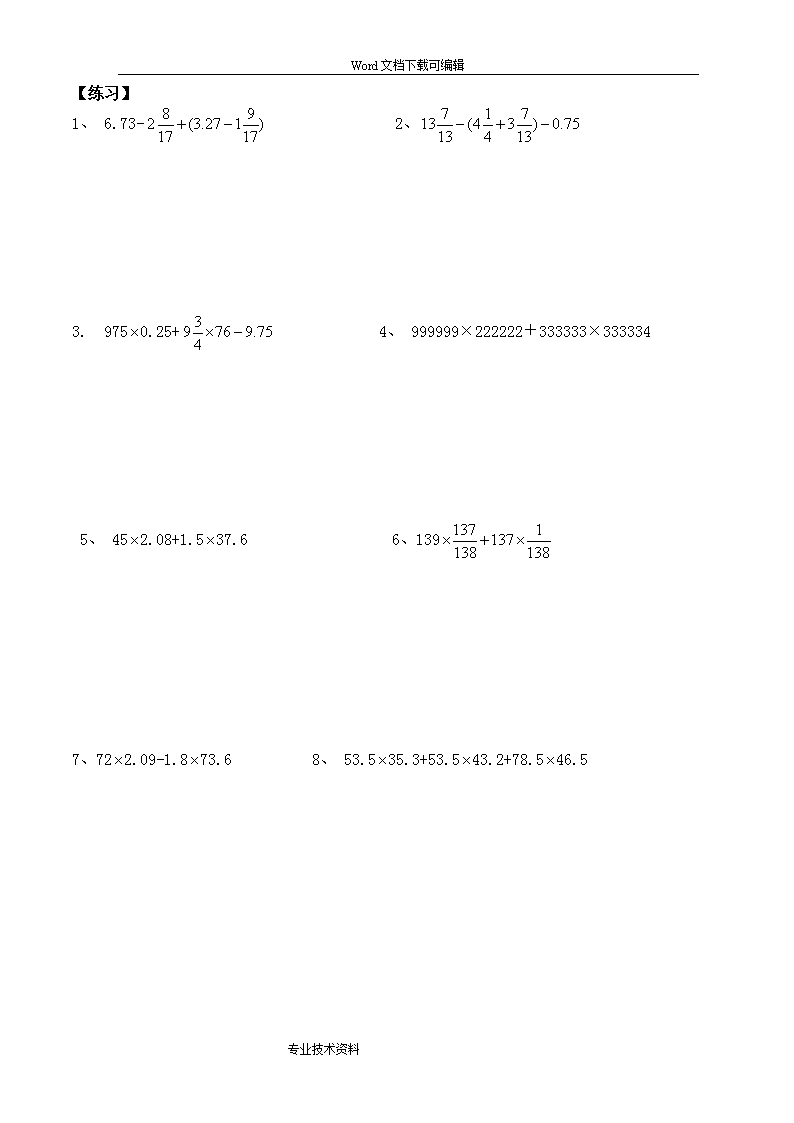小升初计算专项练习 23页

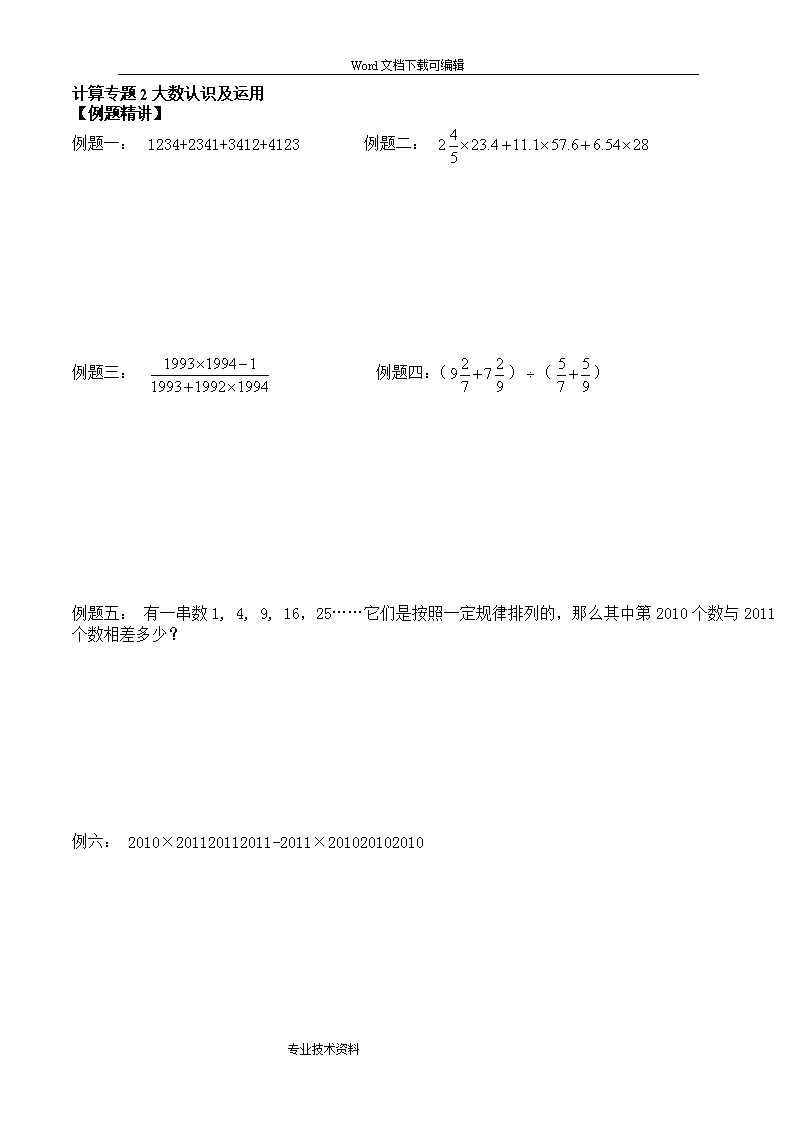
Word文档下载可编辑教师寄语：【“勤”是先苦後甘，“懒”是先甘後苦，後果完全相反，你选择哪个？】天才=99％的汗水＋1％的灵感　小升初计算专项练习在小学计算题中有好多题型方法新颖独特，在升重点中学考试和进入中学分班考试中，多有出现，有的学生因为没见过这种题型常常得分很少或得零分，其实这种题型只要掌握一定的解题方法和规律一点都不难。下面老师跟你支支招：计算专题1小数分数运算律的运用：【例题精选】例题一：4.75+9.63+（8.25-1.37）例题二：例题三：例题四：361.09+1.267.3例题五：81.515.8+81.551.8+67.618.5专业技术资料\nWord文档下载可编辑【练习】1、6.73-2、3.9750.25+4、999999×222222＋333333×3333345、452.08+1.537.66、1397、722.09-1.873.68、53.535.3+53.543.2+78.546.5专业技术资料\nWord文档下载可编辑计算专题2大数认识及运用【例题精讲】例题一：1234+2341+3412+4123例题二：例题三：例题四：（）（）例题五：有一串数1,4,9,16，25……它们是按照一定规律排列的，那么其中第2010个数与2011个数相差多少？例六：2010×201120112011-2011×201020102010专业技术资料\nWord文档下载可编辑【综合练习】1、23456+34562+45623+56234+623452、3、9999977776+33333666664、20122－201125、999274+62746、（）（）7、123456789×987654321-123456788×987654322专业技术资料\nWord文档下载可编辑计算专题3分数专题【例题精讲】例题一：27例题二：例题三：例题四：例题五：【综合练习】1、732、3、专业技术资料\nWord文档下载可编辑4、5、6、7、8、计算专题4列项求和【例题精讲】例题一：例题二：例题三：例题四：专业技术资料\nWord文档下载可编辑例题五：（）（）-（）（）【综合练习】1、2、3、4、5、6、专业技术资料\nWord文档下载可编辑7、计算专题5计算综合【例题精讲】例题一：例题二：111111111111111111例题三：例题四：专业技术资料\nWord文档下载可编辑例题五：从2000到6999这5000个数中数字只和能被5整除的数一共有多少个？例六：100+99—98—97+96+95—94—93……+4+3—2—1例七：【综合练习】1、2、专业技术资料\nWord文档下载可编辑3、4、5、（1+3+5+7+…+1999）-（2+4+6+8+…+1998）6、7、（＋）＋（＋＋）＋（＋＋＋）＋…＋（＋＋＋＋…＋）计算专题6超大数的巧算熟记规律，常能化难为易。1、25×4=100，②125×8=1000，③=0.25=25%，④=0.75=75%,⑤=0.125=12.5%,⑥=0.375=37.5%,⑦=0.625=62.5%,⑧=0.875=87.5%利用①12321=111×111，1234321=1111×1111，123454321=11111×11111②123123=123×1001，12341234=1234×10001③12345679×9=111111111等规律巧解题：专业技术资料\nWord文档下载可编辑×108÷3620102010×1999-2010×1999199912345679×63=72×12345679=计算专题7利用积不变、拆数和乘法分配率巧解计算题：28.67×67+3.2×286.7+573.4×0.05314×0.043+3.14×7.2-31.4×0.1541.2×8.1+11×9.25+53.7×1.919931993×1993-19931992×1992-19931992专业技术资料\nWord文档下载可编辑1.993×1993000+19.92×199200-199.3×19920-1992×1991333×332332333-332×333333332计算专题8牢记设字母代入法（1+0.21+0.32）×（0.21+0.32+0.43）-（1+0.21+0.32+0.43）×（0.21+0.32）（1+0.23+0.34）×（0.23+0.34+0.65）-（1+0.23+0.34+0.65）×（0.23+0.34）专业技术资料\nWord文档下载可编辑（1+++）×（+++）-（1++++）×（++）（+++）×（+++）-（++++）×（++）（++）×（++）-（+++）×（+）计算专题9利用a÷b=巧解计算题：①6.4×480×33.3）÷（3.2×120×66.6）（+）÷（+）专业技术资料\nWord文档下载可编辑计算专题10利用裂项法巧解计算题+++……++++……++++++1×2+2×3+3×4+……99×1001×2×3+2×3×4+3×4×5+……+9×10×11计算专题11(递推法或补数法)1.2.+++++……++.专业技术资料\nWord文档下载可编辑+++++计算专题12．斜着约分更简单（1+）×（1+）（1+）×……×（1+）（1+）（1-）×（1-）（1-）×……×（1-）（1-）计算专题13定义新运算1.规定a☉b=,则2☉(5☉3)之值为     .2.如果1※4=1234,2※3=234,7※2=78,那么4※5=       .专业技术资料\nWord文档下载可编辑3.[A]表示自然数A的约数的个数.例如,4有1,2,4三个约数,可以表示成[4]=3.计算:[120]=       .4.规定新运算a※b=3a-2b.若x※(4※1)=7,则x=       .5.两个整数a和b,a除以b的余数记为a☆b.例如,13☆5=3,5☆13=5,12☆4=0.根据这样定义的运算,(26☆9)☆4=       .6.规定:6※2=6+66=72,2※3=2+22+222=246, 1※4=1+11+111+1111=1234.7※5=    .7.规定:符号“△”为选择两数中较大数,“☉”为选择两数中较小数.例如:3△5=5,3☉5=3.那么,[(7☉3)△5]×[5☉(3△7)]=       .计算专题14解方程专业技术资料\nWord文档下载可编辑计算专题15等差数列11011．若干个数排成一列称为数列，数列中的每一个数称为一项，其中第一项称为首项，最后一项称为未项，数列中的个数称为项数，从第二项开始，后项与前项之差都相等的数列称，如“等差数列”后项与前项的差称为公差。例如：、3、5、7、9、…97、99、首项末项每两个数之间相差为2，即公差为2。共有51个数，即项数为51。2．需要牢记的公式（1）未项=首项+（项数-1）×公差，根据此公式，又可推出：首项=末项-（项数-1）×公差项数=（末项-首项）÷公差+1（2）数列和=（首项+末项）×项数÷2【典型例题】例1已知等差数列5，8，11，14，17，…，它的第25项是什么？第42项呢？例2已知等差数列7，12，17，…，122，问这个等差数列共有多少项？例3某礼堂里共有21排座位，从第一排座位开始，以后每一排比前一排多4个座位，最后一排有100个座位，问这个礼堂一共有多少个座位？专业技术资料\nWord文档下载可编辑例4（1）1+3+5+7+…+2007（2）2007-3-6-9-…-51-54例5（2+4+6+…+100）-（1+3+5+…+99）例61001个队员参加数学奥林匹克竞赛，每两个队员握一次手，他们握了多少次手？计算专题16尾数与完全平方数尾数问题常用到的结论：（1）相邻两个自然乘积的个位数字只能是0，2，6。（2）完全平方数的尾数只能是0，1，4，5，6，9。例1求3＋33＋333＋…＋的和的末一位数是几？末两位是几？专业技术资料\nWord文档下载可编辑例2求的尾数是多少？例3的个位数字是多少？例4199加上一个两位数，使结果是完全平方数，这样的两位数一共有几个？例5已知有3个数：1□9，3□32，6□6其中哪几个可以写成完全平方数？专业技术资料\nWord文档下载可编辑计算专题17加法原理、乘法原理例1有1元、2元、5元人民币各一张，可以从中组成多少种币值的人民币？例2将3封信投到4个邮筒中，一个邮筒最多投一封信，有种不同的方法。例3用0，1，2，3这四个数字组成三位数，其中：（1）有多少个没有重复数字的三位数？（2）有多少个不同的三位数？（3）有多少个没有重复数字的三位偶数？（4）有多少个没有重复数字，且为3的倍数的三位数？专业技术资料\nWord文档下载可编辑计算专题18分数的估算求值例1在下列□内填两个相邻的整数，使不等式成立．□<□例2已知求A的整数部分是多少？例3老师在黑板上写了13个自然数，让小明计算平均数（保留两位小数），小明计算的答案是12.43，老师说最后一位数字错了，其它的数字都对，正确的答案应该是什么？例4有一本书中间被撕掉了一张，余下各页码之和是1248，被撕掉的那一张上的页码是多少？计算专题19简单数论1．能被2，5整除的数的特点:末一位能被2，5整除；2．能被3，9整除的数的特点：各位数字之和能被3，9整除；3．能被7，13整除的数的特点：末三位与末三位之前的数的差能被7或13整除；专业技术资料\nWord文档下载可编辑4．能被11整除的数的特点：奇位数字之和与偶位数字之和的数的差能被11整除；5．能被4，25整除的数的特点：末两位被4，25整除；6．能被8，125整除的数的特点：末三位能被8或125整除．例1利用1～9中的数，分别组成两个能被3整除的五位数；两个能被9整除的三位数，，；两个能被11整除的四位数，．例2有一种长方形的砖，每块长30厘米，宽18厘米，至少用多少块这样的砖才能铺成一个正方形?例3两个数相除，商是8，余数也是8，被除数，除数商及余数的和为159，求被除数和除数?例4三个连续的自然数之积为504，这三个数分别是（），（），（）．奥数专题20周期问题例1．在下表中,每列的一个字母和一个字为一组,如第一组为“A学”,第二组为“B习”…第25组是多少?ABCDABCD…学习好学习好学习…例2．今年的6月1号是星期天，那么今年的9月20是星期几呢？例3.,求小数点后面的2008位数是什么数?小数点后的2008位数字之和是多少?例4．数手指：大拇指为1,食指为2,中指为3,无名指为4,小拇指为5,然后换方向,无名指为6,中指为7,食指为8,大拇指为9,再换向,食指为10…,这样数到1998时应该停在哪个手指上面呢？专业技术资料\nWord文档下载可编辑专业技术资料