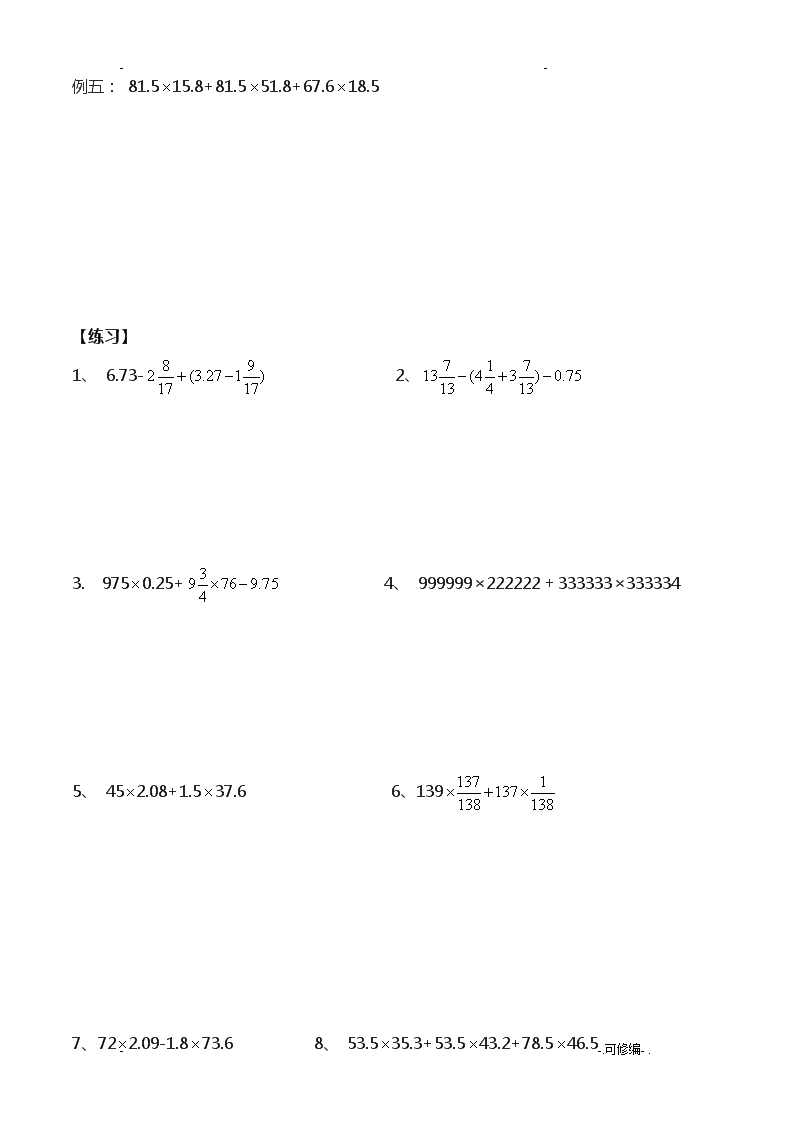小升初数学计算分类专题 21页

--计算综合计算专题1小数分数运算律的运用：计算专题2大数认识及运用计算专题3分数专题计算专题4裂项求和计算专题5计算综合计算专题6换元法计算专题7定义新运算计算专题8解方程计算专题9等差数列计算专题10加法原理、乘法原理--.可修编-.\n--计算专题1小数分数运算律的运用：【例精选】例一：4.75+9.63+〔8.25-1.37〕例二：例三：例四：361.09+1.267.3--.可修编-.\n--例五：81.515.8+81.551.8+67.618.5【练习】1、6.73-2、3.9750.25+4、999999×222222＋333333×3333345、452.08+1.537.66、1397、722.09-1.873.68、53.535.3+53.543.2+78.546.5--.可修编-.\n--计算专题2大数认识及运用【例精讲】例一：1234+2341+3412+4123例二：例三：例四：〔〕〔〕例五：有一串数1,4,9,16，25……它们是按照一定规律排列的，那么其中第2010个数与2011个数相差多少？--.可修编-.\n--例六：2010×1-2011×0【综合练习】1、23456+34562+45623+56234+623452、3、9999977776+33333666664、20122－201125、999274+62746、〔〕〔〕7、123456789×98765488×987654322--.可修编-.\n--计算专题3分数专题【例精讲】例一：27例二：例三：例四：例五：【综合练习】--.可修编-.\n--1、732、3、4、5、6、7、8、计算专题4裂项求和【例精讲】例一：例二：--.可修编-.\n--例三：例四：【综合练习】1、2、3、4、--.可修编-.\n--5、6、计算专题5计算综合【例精讲】例一：--.可修编-.\n--例二：111111111111111111例三：例四：例五：从2000到6999这5000个数中数字只和能被5整除的数一共有多少个？例六：100+99—98—97+96+95—94—93……+4+3—2—1--.可修编-.\n--例七：【综合练习】1、2、3、4、--.可修编-.\n--5、〔1+3+5+7+…+1999〕-〔2+4+6+8+…+1998〕6、7、〔＋〕＋〔＋＋〕＋〔＋＋＋〕＋…＋〔＋＋＋＋…＋〕--.可修编-.\n--计算专题6换元法〔1+0.21+0.32〕×〔0.21+0.32+0.43〕-〔1+0.21+0.32+0.43〕×〔0.21+0.32〕〔1+0.23+0.34〕×〔0.23+0.34+0.65〕-〔1+0.23+0.34+0.65〕×〔0.23+0.34〕--.可修编-.\n--〔1+++〕×〔+++〕-〔1++++〕×〔++〕〔+++〕×〔+++〕-〔++++〕×〔++〕〔++〕×〔++〕-〔+++〕×〔+〕--.可修编-.\n--计算专题7定义新运算1.规定a☉b=,那么2☉(5☉3)之值为     .2.如果1※4=1234,2※3=234,7※2=78,那么4※5=       .3.[A]表示自然数A的约数的个数.例如,4有1,2,4三个约数,可以表示成[4]=3.计算:[120]=       .4.规定新运算a※b=3a-2b.假设x※(4※1)=7,那么x=       .5.两个整数a和b,a除以b的余数记为a☆b.例如,13☆5=3,5☆13=5,12☆4=0.根据这样定义的运算,(26☆9)☆4=       .6.规定:6※2=6+66=72,2※3=2+22+222=246,--.可修编-.\n-- 1※4=1+11+111+1111=1234.7※5=    .7.规定:符号“△〞为选择两数中较大数,“☉〞为选择两数中较小数.例如:3△5=5,3☉5=3.那么,[(7☉3)△5]×[5☉(3△7)]=       .--.可修编-.\n--计算专题8解方程--.可修编-.\n--计算专题9等差数列需要牢记的公式〔1〕末项=首项=项数=〔2〕数列和=--.可修编-.\n--【典型例】例1等差数列5，8，11，14，17，…，它的第25项是什么？第42项呢？例2等差数列7，12，17，…，122，问这个等差数列共有多少项？例3某礼堂里共有21排座位，从第一排座位开场，以后每一排比前一排多4个座位，最后一排有100个座位，问这个礼堂一共有多少个座位？例4〔1〕1+3+5+7+…+2007〔2〕2007-3-6-9-…-51-54例5〔2+4+6+…+100〕-〔1+3+5+…+99〕例61001个队员参加数学奥林匹克竞赛，每两个队员握一次手，他们握了多少次手？--.可修编-.\n--计算专题10加法原理、乘法原理例1用1角、2角和5角的三种人民币〔每种的数没有限制〕组成1元钱，有多少种方法？例2将3封信投到4个邮筒中，一个邮筒最多投一封信，有种不同的方法。例3一把钥匙只能开一把锁，现在有10把钥匙和10把锁全部都搞乱了，最多要试验多少次才能全部配好锁和相应的钥匙？例4某人到食堂去买饭菜，食堂里有4种荤菜，3种蔬菜，2种汤。他要各买一样，共有多少种不同的买法？--.可修编-.\n--例5从5幅国画，3幅油画，2幅水彩画中选取两幅不同类型的画布置教室，问有几种不同的选法？例6有两个一样的正方体，每个正方体的6个面上分别标有数字1，2，3，4，5，6。将两个正方体放在桌面上，向上的一面数字之和为偶数的有多少种情形？--.可修编-.----.可修编-.