初中数学_概率及统计题知识点汇总_中考 17页

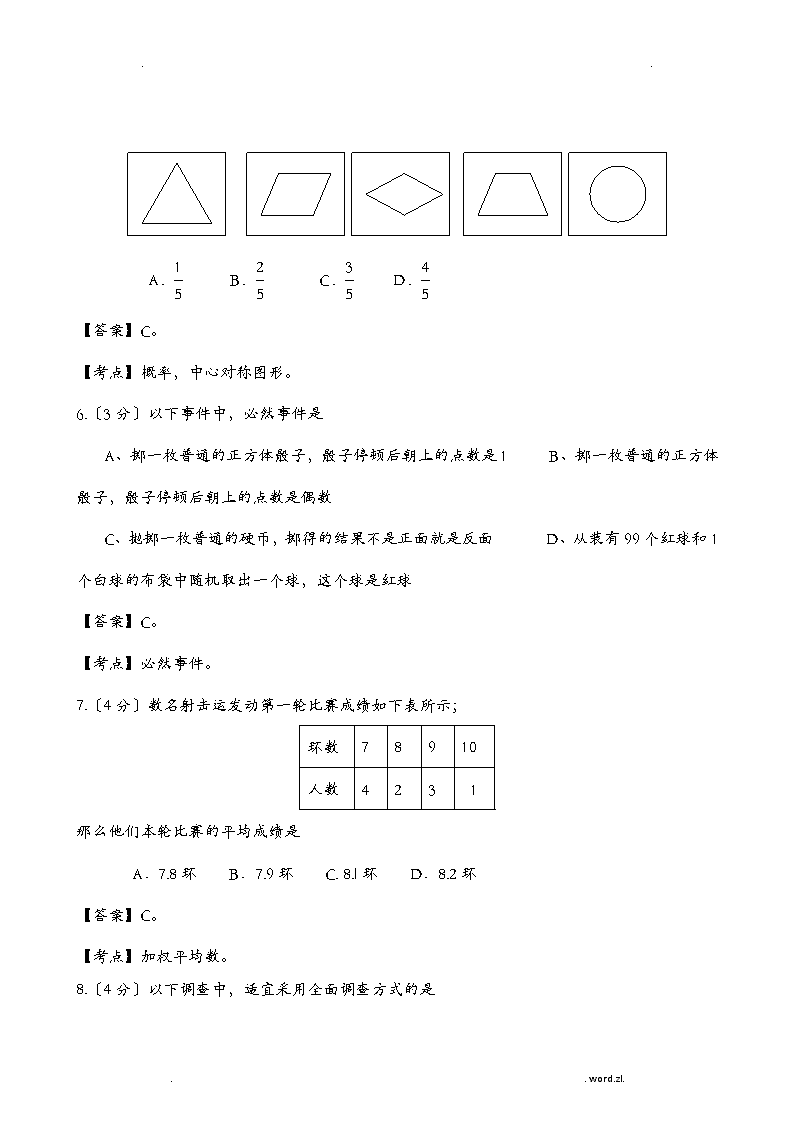
..中考数学统计与概率试题汇编一、选择题1.〔4分〕从1，2，﹣3三个数中，随机抽取两个数相乘，积是正数的概率是A、0B、C、D、12.〔3分〕以下事件为必然事件的是A、翻开电视机，它正在播广告B、抛掷一枚硬币，一定正面朝上C、投掷一枚普通的正方体骰子，掷得的点数小于7D、某彩票的中奖时机是1%，买1一定不会中奖3.〔3分〕以下事件中，属于必然事件的是A．翻开电视机，它正在播广告B．翻开数学书，恰好翻到第50页C．抛掷一枚均匀的硬币，恰好正面朝上D．一天有24小时【答案】D。【考点】必然事件。4.〔3分〕九年级一班5名女生进展体育测试，她们的成绩分别为70，80，85，75，85〔单位：分〕，这次测试成绩的众数和中位数分别是A．79，85B．80，79C．85，80D．85，85【答案】C。【考点】众数，中位数。5.〔4分〕有5形状、大小、质地均一样的卡片，反面完全一样，正面分别印有等边三角形、平行四边形、菱形、等腰梯形和圆五种不同的图案．将这5卡片洗匀后正面朝下放在桌面上，从中随机抽出一，抽出的卡片正面图案是中心对称图形的概率为..word.zl.\n..A．B．C．D．【答案】C。【考点】概率，中心对称图形。6.〔3分〕以下事件中，必然事件是A、掷一枚普通的正方体骰子，骰子停顿后朝上的点数是1B、掷一枚普通的正方体骰子，骰子停顿后朝上的点数是偶数C、抛掷一枚普通的硬币，掷得的结果不是正面就是反面D、从装有99个红球和1个白球的布袋中随机取出一个球，这个球是红球【答案】C。【考点】必然事件。7.〔4分〕数名射击运发动第一轮比赛成绩如下表所示；环数78910人数4231那么他们本轮比赛的平均成绩是A．7.8环B．7.9环C.8.l环D．8.2环【答案】C。【考点】加权平均数。8.〔4分〕以下调查中，适宜采用全面调查方式的是..word.zl.\n..A．了解市的空气质量情况B．了解闽江流域的水污染情况C．了解市居民的环保意识D．了解全班同学每周体育锻炼的时间【答案】D。【考点】全面调查与抽样调查。9.〔4分〕以下说法错误的选项是A．必然事件发生的概率为1B．不确定事件发生的概率为0.5C．不可能事件发生的概率为0D．随机事件发生的概率介于0和1之间【答案】B。【考点】概率的意义。10.〔4分〕“是实数，〞这一事件是.A.必然事件B.不确定事件C.不可能事件D.随机事件【答案】A。【考点】必然事件。二、填空题1.〔4分〕地球外表陆地面积与海洋面积的比约为3：7．如果宇宙中飞来一块陨石落在地球上，那么落在陆地上的概率是　▲　．【答案】。【考点】几何概率。2.〔4分〕口袋中有2个红球和3个白球，每个球除颜色外完全一样，从口袋中随机摸出一个红球的概率是_▲．【答案】。..word.zl.\n..【考点】概率。3.〔4分〕甲、乙两个参加某市组织的省“农运会〞铅球工程选拔赛，各投掷6次，记录成绩，计算平均数和方差的结果为：甲＝13.5m，乙＝13.5m，S2甲＝0.55，S2乙＝0.5０，那么成绩较稳定的是▲〔填“甲〞或“乙〞〕.【答案】乙。【考点】方差。4.〔4分〕某年6月上旬，市最高气温如下表所示：日期12345678910最高气温〔℃〕30283032343127323330那么，这些日最高气温的众数为▲℃．【答案】30。【考点】众数。【5.〔3分〕一组数据10，14，20，24．19，16的极差是▲。【答案】14。【考点】极差。6.〔3分〕袋子中有3个红球和6个白球，这些球除颇色外均完全一样，那么从袋子中随机摸出一个球是白球的概率是▲，【答案】。【考点】概率。7.〔4分〕数据的平均数是1，那么这组数据的中位数是▲。【答案】1。..word.zl.\n..【考点】中位数，算术平均数。8.〔3分〕抛掷一枚质地均匀的硬币两次，正面都朝上的概率是_▲．【答案】。【考点】列表法或树状图法，概率。9.〔3分〕某次跳绳比赛中，统计甲、乙两班学生每分钟跳绳的成绩〔单位：次〕情况如下表：班级参加人数平均次数中位数方差甲45135149180乙45135151130以下三个命题：〔1〕甲班平均成绩低于乙班平均成绩；〔2〕甲班成绩的波动比乙班成绩的波动大；〔3〕甲班成绩优秀人数少于乙班成绩优秀人数〔跳绳次数≥150次为优秀〕其中正确的命题是_▲．〔只填序号〕【答案】②③。【考点】算术平均数，方差，中位12345678910-次环78910数。10.〔3分〕甲、乙俩射击运发动进展10次射击，甲的成绩是7，7，8，9，8，9，10，9，9，9，乙的成绩如下图.那么甲、乙射击成绩的方差之间关系是▲(填“＜〞，“＝〞，“＞〞)．【答案】＜。..word.zl.\n..三、解答题1.〔10分〕在完毕了380课时初中阶段数学容的教学后，唐教师方案安排60课时用于总复习，根据数学容所占课时比例，绘制如下统计图表〔图1～图3〕，请根据图表提供的信息，答复以下问题：〔1〕图1中“统计与概率〞所在扇形的圆心角为度；〔2〕图2、3中的,；〔3〕在60课时的总复习中，唐教师应安排多少课时复习“数与代数〞容？【答案】解：〔1〕36。〔2〕60；14。〔3〕依题意，得45%×60=27。答：唐教师应安排27课时复习“数与代数〞容。【考点】扇形统计图，统计表，条形统计图，频数、频率和总量的关系。【〔3〕根据频数、频率和总量的关系用60乘以45%即可。2.〔9分〕..word.zl.\n..四小卡片上分别写有数字1、2、3、4．它们除数字外没有任何区别，现将它们放在盒子里搅匀．〔1〕随机地从盒子里抽取一，求抽到数字2的概率；〔2〕随机地从盒子里抽取一．不放回再抽取第二．请你用画树状图或列表的方法表示所有等可能的结果，并求抽到的数字之和为5的概率．【答案】解：〔1〕P〔抽到数字2〕=。〔2〕画树状图：从图可知，两次抽取小卡片抽到的数字之和共有12种等可能的结果，其中抽到的数字之和为5的有4种，∴P〔抽到的数字之和为5〕=。【考点】列表法或树状图法，概率。3.〔9分〕心理安康是一个人安康的重要标志之一．为了解学生对心理安康知识的掌握程度，某校从800名在校学生中，随机抽取200名进展问卷调查，并按“优秀〞、“良好〞、“一般〞、“较差〞四个等级统计，绘制成如下的频数分布表和频数分布直方图．程度频数频率优秀600.3良好100[来源:学&科&网]..word.zl.\n..一般0.15较差[来源:学#科#网]0.05请根据图表提供的信息，解答以下问题：〔1〕求频数分布表中、、的值．并补全频数分布直方图；〔2〕请你估计该校学生对心理安康知识掌握程度到达“优秀〞的总人数．【答案】解：〔1〕∵抽样的总人数为60÷0.3=200，∴=100÷200=0.5；=200×0.15=30；=200×0.05=10。根据较差的频数为10补全频数分布直方图：〔2〕∵800×0.3=240，∴估计该校学生对心理安康知识掌握程度到达“优秀〞的总人数为240人。【考点】频数〔率〕分布表，频数分布直方图，频数、频率和总量的关系，用样本估计总体。4.〔8分〕市某中学对全校学生进展文明礼仪知识测试，为了解测试结果，随机抽取局部学生的成绩进展分析，将成绩分为三个等级：不合格、一般、优秀，并绘制成如下两幅统计图〔不完整〕．请你根据图中所给的信息解答以下问题：..word.zl.\n..优秀50%一般______不合格20%1224364860不合格一般优秀72成绩等级人数〔1〕请将以上两幅统计图补充完整；〔2〕假设“一般〞和“优秀〞均被视为达标成绩，那么该校被抽取的学生中有_▲人达标；〔3〕假设该校学生有1200人，请你估计此次测试中，全校达标的学生有多少人？【答案】解：〔1〕将两幅统计图补充完整：〔2〕96．〔3〕1200×(50%＋30%)＝960〔人〕答：估计全校达标的学生有960人。【考点】扇形统计图，条形统计图，频数、频率和总量的关系，用样本估计总体。5.〔10分〕某校为庆祝中国共产党90周年，组织全校1800名学生进展党史知识竞赛．为了解本次知识竞赛成绩的分布情况，从中随机抽取了局部学生的成绩进展统计分析，得到如下统计表：分组频数频率..word.zl.\n..59.5～69.530.0569.5～79.512a79.5～89.5b0.4089.5～100.5210.35合计c1根据统计表提供的信息，答复以下问题：〔1〕a=，b=，c=；〔2〕上述学生成绩的中位数落在组围；〔3〕如果用扇形统计图表示这次抽样成绩，那么成绩在89.5～100.5围的扇形的圆心角为度；〔4〕假设竞赛成绩80分〔含80分〕以上的为优秀，请你估计该校本次竞赛成绩优秀的学生有人．【答案】解：〔1〕0.2，24，60。〔2〕79.5～89.5。〔3〕126°。〔4〕1350．【考点】频数〔率〕分布表，频数、频率和总量的关系，中位数，扇形统计图的圆心角，用样本估计总体。6.〔8分〕甲袋中有三个红球，分别标有数字1、2、3；乙袋中有三个白球，分别标有数字2、3、4．这些球除颜色和数字外完全一样．小明先从甲袋中随机摸出一个红球，再从乙袋中随机摸出一个白球．请画出树状图，并求摸得的两球数字一样的概率．..word.zl.\n..【答案】解：画树状图：图中可见，共有9种等可能的结果，数字一样的有2种，∴P〔两个球上的数字一样〕＝。【考点】树状图法，概率。7.〔10分〕为庆祝建党90周年，某校团委方案在“七·一〞前夕举行“唱响红歌〞班级歌咏比赛，要确定一首喜欢人数最多的歌曲为每班必唱歌曲。为此提供代号为A、B、C、D四首备选曲目让学生选择，经过抽样调查，并将采集的数据绘制如下两幅不完整的统计图。请根据图①，图②所提供的信息，解答以下问题：〔1〕本次抽样调查的学生有_________名，其中选择曲目代号为A的学生占抽样总数的百分比是________%；〔2〕请将图②补充完整；〔3〕假设该校共有1200名学生，根据抽样调查的结果估计全校共有多少名学生选择此必唱歌曲？〔要有解答过程〕..word.zl.\n..【答案】解：〔1〕180；20%。〔2〕∵选C的有180－36－30－42=72〔人〕，∴据此补图：〔3〕∵喜欢人数最多的歌曲为每班必唱歌曲，代号为C的曲目喜欢人数最多，为72人，∴喜欢C曲目的人数占抽样人数的百分比为72÷180=40%。∴估计全校选择此必唱歌曲共有：1200×40%=480〔名〕。【考点】条形统计图，扇形统计图，频数、频率和总量的关系，用样本估计总体、8.〔8分〕“国际无烟日〞降临之际．小敏同学就一批公众对在餐厅吸烟所持的三种态度(彻底禁烟、建立吸烟室、其他)进展了调查．并把调查结果绘制成如图1、2的统计图．请根据下面图中的信息答复以下问题：..word.zl.\n..〔1〕(2分)被调查者中，不吸烟者中赞成彻底禁烟的人数有____________人：〔2〕(2分)本次抽样凋查的样本容量为____________〔3〕(2分)被调查者中．希望建立吸烟室的人数有____________人；〔4〕(2分)某市现有人口约300万人，根据图中的信息估计赞成在餐厅沏底禁烟的人数约有____________万人．【答案】解：〔1〕82。〔2〕200。〔3〕56。〔4〕159。【考点】条形统计图，扇形统计图，频数、频率和总量的关系，用样本估计总体。9.〔10分〕在“5·12防灾减灾日〞之际，某校随机抽取局部学生进展“平安逃生知识〞测验根据这局部学生的测验成绩〔单位：分〕绘制成如下统计图〔不完整〕：频数分布表频数分布直方图分组频数2468106012分数频数/人0141618708090100频率60≤x＜7020.0570≤x＜801080≤x＜900.4090≤x≤100120.30..word.zl.\n..合计1.00请根据上述图表提供的信息，完成以下问题：〔1〕分别补全频数分布表和频数分布直方图；〔2〕假设从该校随机1名学生进展这项测验，估计其成绩不低于80分的概率约为_▲．分组频数频率60≤x＜7020.0570≤x＜80100.2580≤x＜90160.4090≤x≤100120.30合计401.00【答案】解：〔1〕补全频数分布表和频数分布直方图如下：2468106012分数频数/人0141618708090100〔2〕0.7。【考点】频数〔率〕分布表，频数分布直方图，频数、频率和总量的关系，概率。10.〔8分〕据讯：?省第六次全国人口普查主要数据公报?显示，全省常住人口为36894216人.人口地区分布的数据如图1.另外，我省区域面积分布情况如图2.XX省常住人口地区分布统计图福莆泉厦漳龙三XX州田州门州岩明平德8006004002000712278481256265250353人口/万人地区单位：万平方千米XX省区域面积分布统计图XX1.34XX1.13XX1.22XX0.41XX1.29XX0.17XX1.90XX2.30XX2.62..word.zl.\n..图2图1⑴全省常住人口用科学记数法表示为：___________人〔保存四个有效数字〕.⑵假设人口占全省常住人口22.03%，占7.64%，请补全图1统计图；⑶全省九地市常住人口这组数据的中位数是_________万人；⑷全省平均人口密度最大的是_______市，达_____人/平方千米.〔平均人口密度＝常住人口数÷区域面积，结果准确到个位〕【答案】解：⑴3.689×107。⑵人口36894216×22.03%≈813万人，人口36894216×7.64%≈282万人。据此补全条形统计图如下：⑶282。⑷，2076。【考点】条形统计图，面积分布统计图，科学记数法，有效数字，频数、频率和总量的关系，中位数。【分析】〔1〕根据科学记数法的定义，科学记数法的表示形式为..word.zl.\n..为整数，表示时关键要正确确定的值以及的值。在确定的值时，看该数是大于或等于1还是小于1。当该数大于或等于1时，为它的整数位数减1；当该数小于1时，－为它第一个有效数字前0的个数〔含小数点前的1个0〕。36894216一共8位，从而36894216=3.6894216×107。有效数字的计算方法是：从左边第一个不是0的数字起，后面所有的数字都是有效数字。所以36894216≈3.689×107。〔2〕根据频数、频率和总量的关系，求出、人口，补全条形统计图。〔3〕中位数是一组数据从小到大〔或从大到小〕重新排列后，最中间的那个数〔最中间两个数的平均数〕。由此将这组数据重新排序为250，256，265，278，282，353，481，712，813，∴中位数为282。〔4〕用平均人口密度＝常住人口数÷区域面积计算各市的平均人口密度比拟即可。1311.〔10分〕如图，均匀的正四面体的各面依次标有1，2，3，4四个数字.小明做了60次投掷试验，结果统计如下：朝下数字1234出现的次数16201410⑴计算上述试验中“4朝下〞的频率是__________；⑵“根据试验结果，投掷一次正四面体，出现2朝下的概率是.〞的说确吗？为什么？⑶随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于4的概率．【答案】解：⑴“4朝下〞的频率：。⑵这种说法是错误的．在60次试验中，“2朝下〞的频率为并不能说明“2朝下〞这一事件发生的概率为．只有当试验的总次数很大时，事件发生的频率才会稳定在相应的事件发生的概率附近。..word.zl.\n..⑶随机投掷正四面体两次，所有可能出现的结果如下：第一次第二次12341〔1，1〕〔2，1〕〔3，1〕〔4，1〕2〔1，2〕〔2，2〕〔3，2〕〔4，2〕3〔1，3〕〔2，3〕〔3，3〕〔4，3〕4〔1，4〕〔2，4〕〔3，4〕〔4，4〕总共有16种结果，每种结果出现的可能性一样，而两次朝下数字之和大于4的结果有10种。∴。【考点】概率的意义和计算，列表或画树状图。..word.zl.