苏科版初中数学中考备考精品教案集 68页

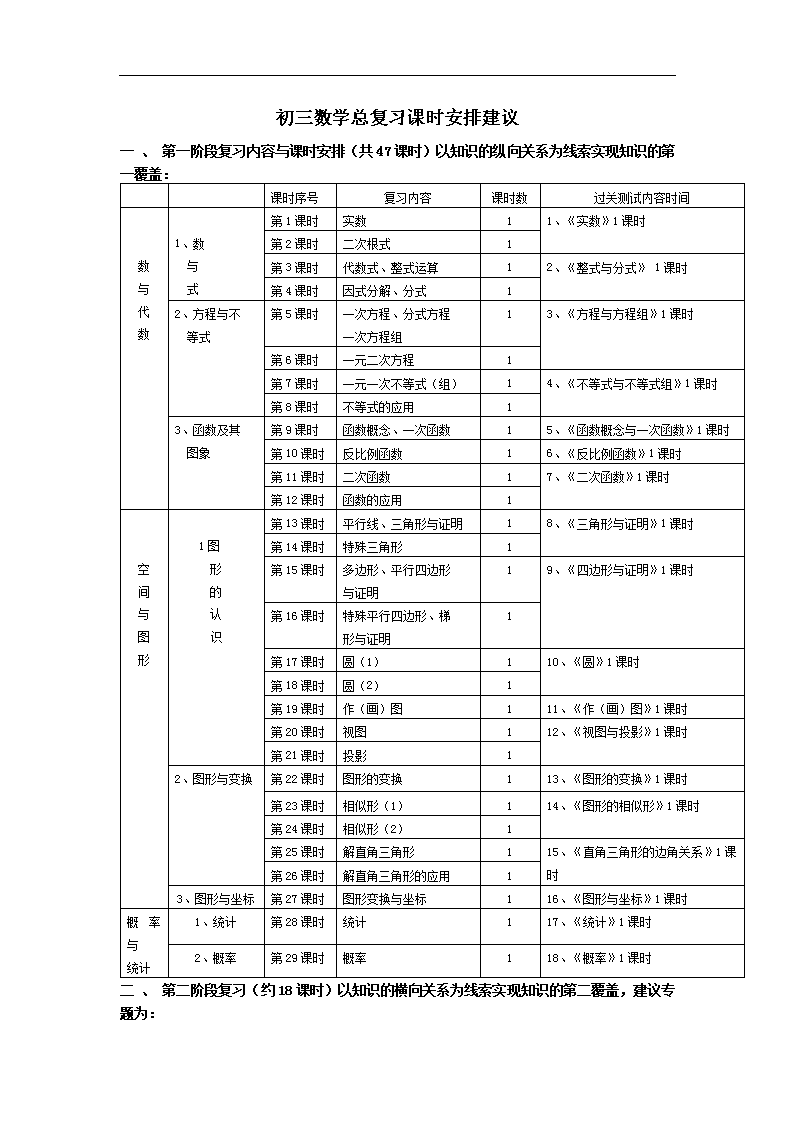
初中数学中考备考精品教案集集体备课成果资料\n初三数学总复习课时安排建议一、第一阶段复习内容与课时安排（共47课时）以知识的纵向关系为线索实现知识的第一覆盖：课时序号复习内容课时数过关测试内容时间数与代数1、数与式第1课时实数11、《实数》1课时第2课时二次根式1第3课时代数式、整式运算12、《整式与分式》1课时第4课时因式分解、分式12、方程与不等式第5课时一次方程、分式方程一次方程组13、《方程与方程组》1课时第6课时一元二次方程1第7课时一元一次不等式（组）14、《不等式与不等式组》1课时第8课时不等式的应用13、函数及其图象第9课时函数概念、一次函数15、《函数概念与一次函数》1课时第10课时反比例函数16、《反比例函数》1课时第11课时二次函数17、《二次函数》1课时第12课时函数的应用1空间与图形1图形的认识第13课时平行线、三角形与证明18、《三角形与证明》1课时第14课时特殊三角形1第15课时多边形、平行四边形与证明19、《四边形与证明》1课时第16课时特殊平行四边形、梯形与证明1第17课时圆（1）110、《圆》1课时第18课时圆（2）1第19课时作（画）图111、《作（画）图》1课时第20课时视图112、《视图与投影》1课时第21课时投影12、图形与变换第22课时图形的变换113、《图形的变换》1课时第23课时相似形（1）114、《图形的相似形》1课时第24课时相似形（2）1第25课时解直角三角形115、《直角三角形的边角关系》1课时第26课时解直角三角形的应用13、图形与坐标第27课时图形变换与坐标116、《图形与坐标》1课时概率与统计1、统计第28课时统计117、《统计》1课时2、概率第29课时概率118、《概率》1课时二、第二阶段复习（约18课时）以知识的横向关系为线索实现知识的第二覆盖，建议专题为：\n1、选择填空2、归纳猜想3、探索开放4、图表信息5、阅读理解6、操作设计7、实践应用8、几何与代数综合三、第三阶段复习：模拟测试（约12课时）实现知识的第三覆盖。第1课实数溧阳市绸缪中学姜龙海复习教学目标：1、理解现实世界中具有相反意义的量的含义，会借助数轴理解实数的相反数和绝对值的意义，会求实数的相反数和绝对值，并会比较实数的大小。2、了解平方根、算术平方根、立方根的概念，会用根号表示数的平方根和立方根。3、了解无理数与实数的概念，知道实数与数轴上的点的一一对应的关系，会用一个有理数估计一个无理数的大致范围，了解近似数与有效数字的概念，会用计算器进行近似计算。4、结合具体问题渗透化归思想，分类讨论的数学思想方法。复习教学过程设计：Ⅰ[唤醒]一、填空：1、-1.5的相反数是、倒数是、绝对值是、1－的绝对值是。2、倒数等于本身的数是，绝对值等于本身的数是。算术平方根等于本身的数是，立方根等于本身的数是。3、2-1=，-2-2=，(-)-2=,(3.14-∏)0=4、在,∏,-,,sin600,tan450中，无理数共有个。5、用科学记数法表示：-3700000=,0.000312=用科学记数法表示的数3.4×105中有个有效数字，它精确到位。6、点A在数轴上表示实数2，在数轴上到A点的距离是3的点表示的数是。7、精确到0.1的近似值为，误差小于1的近似值为。8、比较下列各位数的大小：--,0-1,tan300sin600二、判断：1、不带根号的数都是有理数。（）2、无理数都是无限小数。（）3、是分数，也是有理数。（）4、3-2没有平方根。（）5、若=x，则x的值是0和1。（）6、a2的算术平方根是a。（）三、选择：1、和数轴上的点一一对应的数是（）A、整数B、有理数C、无理数D、实数2、已知：xy＜0，且|x|=3，|y|=1,则x+y的值等于（）A、2或－2B、4或－4C、4或2D、4或－4或2或－23、如果一个数的平方根与立方根相同，这个数为（）A、0B、1C、0或1D、0或+1或-1Ⅱ[尝试]例1，已知下列各数：∏，-2.6，,0,0.4,-(-3),\n,(-)-2,cos300,,-10,0.21221222122221……（按此规律，从左至右，在每相邻的两个1之间，每段在原有2的基础上再增加一个2）。把以上各数分别填入相应的集合。无理数集合：（…）有理数集合：（…）整数结集合：（…）分数集合：（…）正数集合：（…）（解略）提炼：实数的分类思想方法。例2，计算下列各题：1、20-(-)2+2-2-2、(-+-)×(-72)3、()-2-23×0.125-+|-1|2、解略（答案：1：5；2：-11；3：2例3，已知实数a、b在数轴上的位置如图所示：ba（1）你会比较实数a、b的大小吗？（2）你会比较|a|与|b|的大小吗？相信你能！（3）在什么条件下＞0?＜0?=0?并说明此时坐标原点的大致位置。解：（1）a＜b,这是因为在数轴上表示的两个数，右边的总比左边的大。分析：解决问题的关键是数轴的原点的位置，你想按怎样的顺序去变化呢？（可自左向右，也可自右向左）（2）当原点在点a的左边时，|a|＜|b|当原点在点a,b的中点偏左时，|a|＜|b|当原点在点a,b的中点时，|a|＝|b|当原点在点a,b的中点偏右时，|a|＞|b|当原点在点b的右边时，|a|＞|b|（3）当a,b同号时（且a≠0,b≠0），＞0此时坐标原点在a的左侧或b的右侧当a,b异号时（且a≠0,b≠0）＜0此时坐标原点在a,b两点之间当a≠0,b=0时，=0,此时坐标原点在b点提炼：运用绝对值的意义，解决数形结合问题中的动点问题，渗透化归和分类讨论的数学思想方法，训练学生逆向思维。Ⅲ[小结]整数有理数1、实数的分类分数无理数什么叫无理数相反数：2、实数a的绝对值：倒数：（当时）\n3、实数的运算和科学记数法4、运用绝对值的意义，解决数形结合问题中的动点问题，渗透化归和分类讨论的数学思想方法，注意逆向思维的运用。Ⅳ[实践]1、教师自行设计作业复习指导用书P3-41，2，3-，6P171-第2课二次根式绸缪中学戴国琴复习教学目标：1、知道平方根，算术平方根，立方根的含义，能说出二次根式的两条运算法则。2、会用根号表示并会求数的平方根，算术平方根，立方根，会进行简单的二次根式的四则运算，会对简单的二次根式进行化简，能估算一个无理数的大致范围并能比较大小。3、在解题过程中体会数形结合思想，由特殊到一般的数学思想，并能用它们解决问题。复习教学过程设计Ⅰ【唤醒】一、填空：定义：平方根，算术平方根，立方根·=(a≥0,b≥0)化简知识结构（阅读）：运算法则=(a≥0,b＞0)四则运算1．4的平方根是,的算术平方根是,立方根是2．化简：=,=,()2=,×=3．比较大小：3.85,-2-3,4．估算：=（误差小于0.1），=（误差小于1）5．根式分母有理化的结果是二、判断：1．的平方根是（）2.任何数都有算术平方根（）3．任何数都有立方根（）4.×==2()5.=×=2×=()6.5+2=7()三、选择题：1．下列说法中正确的是（）A、1没有算术平方根B、1的平方根是1C、0的平方根是0D、-1的平方根是-12．下列各式中正确的是()\nA、=+5B、=-3C、+=+6D、=-103．下列语句正确的个数为（）(1)+4是64的立方根,（2）=x,（3）的立方根是4,,(4)=+4A、1个B、2个C、3个D、4个4．化简（x<1）正确的是（）A、x-1B、(x-1)2C、1-xD、无法确定Ⅱ【尝试】：例1、计算:(1)-+-(2)-×(3-)(3)(3-2)(5+4)–(–1)2解（略）（答案：-,-,16-40）提炼：（1）对于带根号的无理数的运算，可运用公式·=(a≥0,b≥0),=(a≥0,b＞0)且这两个公式可以顺向和逆向两个方面运用。（2）适当运用乘法公式可使运算简化。（3）计算结果必须简化。例2、是否存在这样的数，它的平方为35？如果不存在，请说明理由，如果存在，请写出来并用作图的方法在数轴上找出表示这个数的实数点。分析：首先求出符合条件的数+,再在数轴上作一个直角三角形,找到表示+的线段即可解（略）提炼：（1）在数轴上作这样的点时，常常通过作直角三角形来解决。（2）本题有两解，防止漏解现象，解题时，应仔细审题，全面考虑，注意数形结合的思想。例3、（1）判断下列各式是否成立，你认为成立的请在括号内打“√”，不成立的打“×”=2()=3()=4()=5()(2)判断完以上各题后，你发现了什么规律？请用含有n的式子将规律表示出来，并注明n的取值范围。（3）请用数学知识说明你所写式子的正确性。\n分析：先按运算公式计算化简后，再判断找规律。解：（1）均正确。（2）=n(n为大于1的自然数)(3)===n提炼：本题是一道探索题，由特殊进行观察，归纳，建立猜想，用符号表示并给出证明，体现了数学中常用的由特殊到一般的思想方法。Ⅲ【小结】：1、知识结构见上表2、基本数学方法：数形结合思想，特殊到一般思想，分类思想等3、解题注意点：（1）解题时应弄清基本概念，法则（2）注意解题的严密性，充分考虑各种情况，防止漏解现象。Ⅳ【实践】：1、教师自行设计2、复习指导用书p3练习一3、(4)(5)p17复习题3、4。第3课代数式整式运算溧阳市燕山中学彭淑霞复习教学目标：1．了解字母表示数的意义，了解单项式、多项式、整式以及单项式的系数与次数、多项式的项与次数、同类项的概念，并能说出单项式的系数和次数、多项式的项和次数。知道正整数幂的运算性质，能说出去括号、添括号法则，了解两个乘法公式的几何背景。2．会用代数式表示简单问题中的数量关系，会求代数式的值，会把一个多项式按某个字母升（降）幂排列，会判断同类项，并能熟练地合并同类项，会准确地进行去括号与添括号，会推导乘法公式，能运用整式的运算性质、公式以及混合运算顺序进行简单的整式的加、减、乘、除运算。3．通过运用幂的运算性质、整式的运算法则和公式进一步发展观察、归纳、类比、概括等能力，会运用类比思想，一般到特殊、再由特殊到一般的数学思想和数形结合思想解决问题。复习教学过程设计：Ⅰ.【唤醒】现实世界、其他学科、数学中的问题情境知识结构（阅读）：\n解决问题整式及其运算一、填空：1．_____和_______统称为整式。2．，，3．整式的混合运算顺序：先________、后________、再________、有括号先____________.二、判断：1．。（）2．。（）3．。（）4.()5．。（）三、选择：1．某商场实行7.5折优惠销售，现售价为y元的商品的原价为（）A.y元B.y元C.元D.元2．（）A.4和3B.2和3C.4和2D.无法确定3．下列各式计算过程正确的是（）A.B.C.D.\n4．下列各式中，不能用平方差公式计算的是（）A.B.C.D.5.()A.4B.8C.4或-4D.8或-8Ⅱ.【尝试】例1．先化简，再求值：。（答案：11）例2．计算：分析：按整式混合运算的顺序：先乘方，同级运算从左往右依次进行。（答案：36b）提炼：在熟练掌握整式的运算法则和幂的运算性质基础上必须严格按照混合运算顺序逐步运算。例3．计算：（1）；（2）分析：第（1）题根据混合运算法则先合理使用乘法公式，后进行整式的加减运算。第（2）题先将原式转化为的形式，后运用平方差公式将其化为的形式，最后利用完全平方公式计算即可。（答案见复习指导用书第11页）提炼：根据乘法公式的特点将原题中的代数式变形为符合公式特点的形式是解此类题的关键。例4．见《复习指导用书》第6页例2分析：解决本题时学生往往着眼于分析表格中的数据的变化，应指导学生结合具体的图形观察图形的形成规律，着重在摆成的平行四边形的两组对边与菱形和等腰梯形的边长之间的关系。提炼：本例是一道探索题，首先给出了几个特殊的图形，然后根据这些特殊的图形的周长，进行探索、归纳、猜想，得到一般图形的周长，体现了数学中常见的由一般到特殊、再由一般到特殊的思想方法以及数形结合思想。Ⅲ.【小结】1．本单元的知识结构（见填空）。2．本节课运用的数学思想方法：类比思想，一般到特殊、再由特殊到一般的思想方法和数形结合思想等。Ⅳ.【实践】1．教师自行设计作业。2．复习指导用书第9页第3、7、8题和第12页第3题。\n第4课时因式分解分式燕山中学王爱军复习教学目标1、知道因式分解、分式的概念；能说出分式的基本性质。2、会灵活应用四种方法进行因式分解；会利用分式基本性质进行约分和通分；会进行简单的分式加、减、乘、除运算。3、会逆用乘法公式、乘法法则验证因式分解；会用类比的方法得出分式的性质和运算法则；会用作差法比较两个代数式值的大小。复习教学过程设计一、【唤醒】1、填空题因式分解因式分解的概念分组分解法十字相乘法因式分解的方法（因式分解方法的选择：一提、二用、三叉、四分组）分式分式的运算分式的概念分式的基本性质（1）（2）因式分解中的公式有，，（3）分式的乘（除）法法则是，分式的加（减）法法则是，2、判断题（1）等式从左到右的变形是分解因式（×）（2）只要分式的分子为零，则分式的值就为零（×）（3）分式有意义，则a≠±1（×）3、选择题（1）若则的值应是（C）A．7B．10C．70D．17（2）下列各式分解不正确的是（C）A、B、C、D、（3）分解因式:的结果是(C)\nA、B、C、D、（4）下列等式成立的是（D）ABCD（5）化简等于（C）A1BCD二、【尝试】例1有这样的一道题：“计算：的值，其中x=2006。”甲同学把“”错抄成“”，但他的计算结果也是正确的。你说这是怎么回事？解原式=0因为化简结果不含x，所以无论他抄什么值，结果都是正确的。提炼：如果把x的值抄错，而不影响计算结果，这一类题的化简结果一定是一个常数，与x的取值无关；如果把x的值抄成它的相反数，而不影响计算结果，这一类题的化简结果一定是一个常数或者是关于x偶次幂的代数式，与x的符号无关。例2化简（1）（2）（）解（1）原式=（2）原式=提炼：（1）解题时要注意分式的运算顺序，先乘除，再加减，有括号优先，其次能分解的多项式要分解因式，便于约分，结果一定要是最简分式。（2）对于分配律仍适用，但不能用分配律。例3已知：，求整式A、B。分析：由于要求A、B，等式的左边是已知，右边是未知，可以从未知化到已知。故把等式作恒等变形，得到等式左右两边分母相同，所以分子也相同，转化为关于A、B的一个二元一次方程组，再求解。解A=1B=2提炼：\n本例是分式运算的逆向运用，两个代数式恒等，首先是化结构相同，其次是利用相同项的系数也相同求未知量。例4甲、乙两人进行百米赛跑，甲前半程的速度为m米/秒，后半程的速度为n米/秒；乙前半时的速度为m米/秒，后半时的速度为n米/秒。问：谁先到达终点？分析：本题首先要用m、n的代数式表示甲、乙两人到达终点的时间t1、t2，比较t1、t2的大小，可以转化为t1-t2与0比较解见复习指导用书第16页提炼：（1）比较两个代数式A、B的值的大小，通常可用作差的方法，当A-B﹥0，则A﹥B；当A-B=0，则A=B；当A-B﹤0，则A﹤B。（2）由于本例中没有指明m、n的大小，所以要分m=n与m≠n两种情况讨论。三、【小结】1、带领学生回顾尝试中的填空题。2、这节课复习因式分解的应用，化简分式。在化简分式时，注意的运算顺序和符号，防止出错。其次比较两个代数式值的大小可以用作差法。四、【实践】（1）教师自行设计作业（2）复习指导：14页第3题单数、17页3、4第5课时一次方程分式方程一次方程组燕山中学居群芳复习教学目标1、了解一次方程、分式方程、二元一次方程组的概念。知道方程组的解的含义。理解分式方程产生增根的原因。理解二元一次方程与一次函数的关系。说出解整式方程和分式方程的异同，2、会解一元一次方程、简单的二元一次方程组、可化为一元一次方程的分式方程。3、运用化归思想，引导学生分析出解二元一次方程组的本质是消元。运用方程或方程组解决实际问题复习教学过程设计一、【唤醒】1、填空：方程（组）的应用分式方程整式方程一元二次方程一元一次方程解题步骤二元一次方程组解法图像法方程解题方法：是\n2、判断：（1）1是一元一次方程（）（2）∵∴（）（3）∵是方程=3的解∴方程=3的解是（）（4）方程组的解是一次函数与的图象的交点坐标（）3、选择：（1）关于的方程是一元一次方程，则为()A、B、C、D、（2）二元一次方程组的解是()A、B、C、D、（3）已知是方程的一个根，则的值是（）A、8B、—8C、0D、2（4）已知方程组的解是，则的值为（）A、3B、0C、D、1二、【尝试】：例1：解方程：（1）（2）解：略答案：（1）（2）是增根，原方程无解提炼：解分式方程与整式方程的方法相似，容易出现错误的地方一是去分母时漏乘整式项及分子是多项式忘记添括号，二是忘记检验求得的整式方程的解是不是分式方程的根；例2：解方程组\n（1）（2）解略答案（1）（2）提炼：解二元一次方程组应先观察方程中相同未知数的系数的特征，如果一个未知数的系数绝对值为1，一般选用代入法，若相同未知数系数绝对值相等，一般用加减法。例3：在一次慈善捐款活动中，某同学对甲、乙两班捐款情况进行统计，得到如下三条信息：信息一：甲班共捐款300元，乙班共捐款232元；信息二：乙班平均每人捐款钱数是甲班平均每人捐款钱数的倍；信息三：甲班比乙班多2人.请你根据以上三条信息，求出甲班平均每人捐款多少元？解略答案5元提炼：列方程解应用题的步骤是一“审”二“设”三“列”四“解”五“答”。在审题过程中，要找出等量关系，设元的方法有两种（直接设元法和间接设元法），列是根据等量关系列出相应的方程（组），在解方程时，还要考虑方程的解是否要检验、是否符合实际意义，最后写上答案例4：（1）、阅读下列表格，求出表中关于的方程的解。方程方程的解（2）、通过阅读上述表格，你能解关于的方程吗？分析：仔细阅读表格，比较以后不难发现方程的相似之处。方程左右两边形式完全相同，只是把其中的未知数换成了某个常数，那么这样的方程可直接得解，因此我们只要把换成这种形式即可。解：∵或经检验是原方程的解。提炼：观察、比较、归纳、猜测是解数学题的重要能力，仔细观察方程结构，将要解的方程化为材料中的方程的形式，体会类比思想。三、【小结】1、知识结构：见填空。2、基本数学思想：化归思想、类比思想、数形结合思想。四、【实践】1、教师自行设计作业。2、复习指导用书：第21页3、24页15、31页9、10、12题。\n第6课时一元二次方程燕山中学王爱军复习教学目标1、知道一元二次方程及其相关概念；了解求方程近似解的方法；能说出列方程解应用题的步骤。2、会灵活应用方程解法解简单的一元二次方程。3、会利用一元二次方程知识解决有关实际问题，能根据具体问题的实际意义检验结果的合理性及分类思想。通过复习方程解法，进一步体会转化思想。复习教学过程设计一元二次方程应用（注意验证解的合理性）近似解直接开方法精确解一、【唤醒】1、填空题2、判断题（1）关于的方程是一元二次方程，则（×）（2）把一元二次方程化成一般形式是（×）（3）方程的左边配成完全平方后所得方程为（×）3、选择题（1）方程根的情况是（B）A、有两个相等实根B、有两个不等实根C、没有实根D、无法确定（2）若一元二次方程两个实数根x1、x2，则的值是（A）A、B、C、D、2（3）关于x的一元二次方程的一个根为，另一根为，则有（A）A、B、C、D、（4）已知，则的值为\n（C）A、1B、1或2C、2D、5二、【尝试】例1用适当方法解下列方程：（1）（2）（3）（4）分析：结合方程特点，四道题的解法依次是直接开方法、分解因式法、公式法、配方法。解略答案见复习指导用书第26页提炼：形如的方程，选择用直接开方法；形如的方程，左边可以因式分解，选择用因式分解法；形如的方程，如果一次项系数是偶数，可以选择用配方法；否则用公式法。例2去年，我国政府为减轻农民负担，决定在5年内免去农业税.某乡镇去年人均上缴农业税25元，预计明年人均上缴农业税为16元，假设这两年降低的百分率相同.（1）求降低的百分率；（2）若小红家有4人，今年小红家减少多少农业税？（3）小红所在的乡约有16000农民，问该乡农民今年减少多少农业税.分析：例题第（1）小题跨度3年，去年、今年、明年，用列表法分析，设降低的百分率是，去年是25元，用表示今年是，明年是，然后根据等量关系列出方程，解出的值；第（2）、（3）题已知的值，分别求代数式的值；解略答案（1）20%（2）20元（3）80000元提炼：运用数学知识解决社会热点问题和实际生活中的问题，关键是理解题意，将实际问题转化为数学问题。其次本例中的百分率是一个小于1的正数。例3有一根长为68cm的铝丝，把它剪成32cm和36cm的两段，用32cm的一段弯成一个矩形，36cm的一段弯成一个有一条边是10cm等腰三角形。请问：能否使弯成的矩形与等腰三角形的面积相等？若不能，请说明原因；若能，请求出矩形的边长。解略解法参照复习指导用书第35页提炼：（1）例题是一道几何背景面积相等的应用题，包含的知识点有矩形、三角形的周长、面积，等腰三角形的三线合一、勾股定理以及方程的解法。（2）三角形一边长是5cm，这一边是腰还是底边不清楚，所以必须分类讨论。例4阅读下列材料，并回答问题：解方程，这是一个一元四次方程，根据该方程特点，它的通常解法是：设，则原方程变为①，解这个方程，得。当时，；当时，。所以原方程有四个根\n（1）在由原方程到方程①的过程中，利用了达到了的目的。（2）利用上述方法解方程：分析：阅读材料，体会换元法解高次方程的方法，设辅助未知量，把方程降次，再解一元二次方程。解（1）换元法降次（2）设，则原方程变为，解这个方程，得。当时，即解得；当时，即，＜0∴此方程无解。所以原方程有两个根提炼：阅读材料，理解解高次方程的一般思路：换元降次，化高次方程为低次方程，体会化归思想。三、【小结】1、带领学生回顾尝试中的填空题。2、本课运用的数学方法有分类思想、化归思想。四、【实践】（1）教师自行设计作业（2）复习指导：28页11、14，38页20第7课一元一次不等式（组）溧阳市燕山中学彭淑霞复习教学目标：1、能根据具体问题中的大小关系了解不等式的意义，能说出不等式的基本性质，知道不等式（组）的解及解集的含义。2、会解简单的一元一次不等式，并能在数轴上表示一元一次不等式的解集；会解一元一次不等式（组），并能在数轴上确定其解集。3、能运用类比思想比较一元一次不等式和一元一次方程在解法上的异同点，初步体会数形结合思想，并能运用数形结合的方法解决与不等式（组）的解集相关的问题。复习教学过程设计：Ⅰ．【唤醒】解集数轴表示一、填空：不等式不等式的基本性质解不等式解集数轴表示知识结构（阅读）：实际背景一元一次不等式解法解集数轴表示一元一次不等式组解法1．不等式基本性质：（1）_________________(2)______________(3)_______________2．不等式的解集在数轴上的表示方法：大于向____画，小于向____画，有等号画____,无等号画______.3.\n解一元一次不等式的一般步骤：（1）______（2）______（3）_____（4）____（5）_____.4．由两个一元一次不等式组成的不等式组的解集一般有四种类型：（1）其解集为_____,简记为“同大取______”.（2）其解集为______,简记为“同小取______”.（3）其解集为______,简记为“大小小大取_____”.（4）其解集为_______,简记为“大大小小_____”.二、判断：1．由得（）2.由得（）3.由得（）4.得（）5.是不等式的一个解（）6.满足不等式的整数解有7个.（）三、选择：1．已知，则下列变形中错误的是()A.B.C.D.2.不等式的解集是()A.B.C.D.3.不等式的非负整数解的个数为（）A.4个B.5个C.6个D.无数个4．不等式的解集为，则的取值范围为（）A.B.C.D.Ⅱ.【尝试】例1．解不等式，并把它的解集在数轴上表示出来。解略。（答案：）\n例1．解不等式组，并求出其整数解。分析：解一元一次不等式组既不能用代入法也不能用加减法，而是分别求出不等式组中的每个不等式的解集，然后利用数轴找出它们解集的公共部分，即不等式组的解集，熟练以后也可以利用口诀“同大取大，同小取小，大小小大取中间，大大小小无解”简捷地确定不等式组的解集。最后结合数轴用列举法确定符合条件的特殊解。解略。（答案：，整数解为1）提炼：用数形结合的思想方法，根据不等式组的解集的概念结合数轴正确确定不等式组的解集及特殊解。例2．若不等式组的解集为，求m的取值范围。分析：首先将不等式组化为，再利用数轴或依据不等式“同大取大”的方法可知。提炼：利用不等式组的解集来确定字母的取值范围，往往需要逆用不等式组的解集，有时需借助数轴或讨论等手段来解决问题。例3．阅读第（1）题的解法，解答第（2）题。（1）解不等式解：①当即时，，所以。②当即时，，所以。综上所述，原不等式的解集为或。（2）根据以上解法和不等式的性质“若，则”解不等式。分析：阅读第（1）题理解其解题方法：根据绝对值的概念先化简绝对值，再解一元一次不等式。解略（答案：或）提炼：运用绝对值的概念化简绝对值，将含绝对值的不等式转化为一元一次不等式，体会分类思想。Ⅲ.【小结】：1.本单元知识结构（见填空第1题）2．本节课运用的数学思想方法：类比思想、数形结合思想、分类思想等。Ⅳ.【实践】1.教师自行设计作业。2.复习指导用书第34页第1、3题。第8课时不等式（组）的应用\n溧阳市燕山中学彭淑霞复习教学目标：1．初步认识一元一次不等式（组）的应用价值，知道在一定条件下的实际问题可以抽象为不等式（组）的问题，并认识到实际问题对不等式（组）的解集的影响，知道一元一次不等式与一次函数有密切的关系。2．能根据具体问题中的数量关系列出一元一次不等式（组），通过解一元一次不等式（组）解决简单的实际问题，并能根据具体问题检查结果是否合理，能通过解一元一次不等式解决简单的一次函数问题。3．类比列方程（组）解应用题的方法经历列一元一次不等式（组）解实际问题的建模过程，体会转化思想，通过解一元一次不等式解决函数问题体会数形结合思想和分类思想。复习教学过程：Ⅰ.【唤醒】一、填空：列一元一次不等式（组）解决实际问题的一般步骤类似于列方程组解应用题的一般步骤，可分为（1）_________（2）根据不等关系列不等式(组)（3）____________(4)__________(5)___________.二、判断：1．一个两位数，十位数字与个位数字的和为6，若这两个两位数不大于42，若设此两位数的个位数字为，则不等式可列为（6-）+≤42。()2．某商店将一个进价80元，标价为120元的商品打折销售，要使得利润率不低于5％，最多可打几折？若设可打折，则不等式可列为120-80≥80×5％.()三、选择：1．使代数式的值不大于的值的的最大整数值为（）A.7B.6C.4D.不存在2．长度为3cm、7cm、cm的三条线段要能围成一个三角形，则x的取值范围为（）A.＜10B.＞4C.4＜＜10D.无法确定3．小新准备用20元钱买钢笔和笔记本，钢笔每支3元，笔记本每本2元，他买了3本笔记本，则他最多还可以买钢笔（）A.6支B.5支C.4支D.3支Ⅱ.【尝试】例1．某校校长暑期将带领该校市级三好学生去北京旅游，甲旅行社说：“如果校长买全票一张，则其余学生可享受半价优惠。”乙旅行社说：“包括校长在内全部按全票价的6折优惠（即按全票价的60％收费）。”若全票价为240元。（1）设学生数为名，甲旅行社收费为元,乙旅行社的收费为\n元，分别计算两家旅行社的收费（建立表达式）。（2）当学生数是多少时，两家旅行社的收费一样？（3）就学生数讨论哪家旅行社更优惠。分析：根据两家旅行社的收费情况构建出一次函数的模型，再根据题意列出不等式求解。也可以画出两个一次函数的图象，通过观察图象比较哪家旅行社更优惠。解答过程见复习指导用书第33页。提炼：在讨论哪家旅行社更优惠时，不能只选特殊的数据代入选择，而要分类讨论。本题主要反映了函数和不等式的关系。本题运用的数学思想方法有分类思想、数形结合思想等等。例2．幼儿园将若干件玩具分给小朋友，如果每人分3件，那么还余59件；如果每人分5件，那么最后一人还少几件，该幼儿园有多少件玩具？有多少个小朋友？分析：设幼儿园有个小朋友，由每人分3件，那么还余59件可知：共有玩具数（3+59）件。由每人分5件，则最后一人还少几件可知：（1）个小朋友每人分5件时玩具数不够，即需要的玩具数>现有的玩具数。则不等式可列为3+59＞5（-1）。（2）（-1）个小朋友每人分5件时玩具数有剩余，即需要的玩具数<现有的玩具数。则不等式可列为3+59＜5。（解答过程见复习指导用书第33页。）提炼：列不等式组解应用题的步骤与列方程组解应用题的步骤类似，不同的是后者寻求的是等量关系，列出的是等式；前者寻求的是不等关系，列出的是不等式，并且解不等式组所得的结果通常是一解集，需要从解集中找出符合题意的答案。例3．某厂用甲、乙两种原料配制成某种饮料，已知这两种原料的维生素C含量及购买这两种原料的价格如下表：原料维生素及价格甲种原料乙种原料维生素C/（单位/千克）600100原料价格/（元/千克）84现配制这种饮料10千克。⑴如果要求饮料至少含有4200单位的维生素C，试写出所需甲种原料（千克）应满足的不等式。⑵在⑴的条件下，如果还要求购买甲、乙两种原料的费用低于72元，那么应在什么范围内购买甲种原料？分析：①由“用甲、乙两种原料配制成某种饮料，现配制这种饮料10千克。”可知：现所需甲种原料为千克，则所需乙种原料为（10-）千克。千克甲种原料中维生素C的含量为600千克，（10-）千克乙种原料中维生素C的含量为100（10-）千克，由题意得：可得：600+100（10-）≥4200。②千克甲种原料的价格为8元，（10-）千克乙种原料的价格为4（10-）元，则购买甲、乙两种原料的费用为：8+4(10-)元，由题意得：8+4(10-)＜72.从而建立不等式组。此不等式组的解集为6.4≤＜8.提炼：本题为调配问题。例4．认真阅读对话：小明：“阿姨，我买一盒饼干和一袋牛奶。”（递上10元钱）\n售货员：“小朋友，本来你用10元钱买一盒饼干是多的，但要再买一袋牛奶就不够了。今天是儿童节，我给你的饼干打9折，两样东西请拿好，还有找你的8角钱。”请你根据对话的内容，试求出饼干和牛奶的标价是多少元（注：饼干的标价是整数元）？分析：设饼干的标价为元。由“本来你用10元买一盒饼干是多的”可建立不等式＜10；由“我给你的饼干打9折，两样东西请拿好，还有找你的8角钱”可知牛奶的标价为（10-0.8-90％）元，由“本来你用10元钱买一盒饼干是多的，但再买一袋牛奶就不够了”建立不等式：+(10-0.8-90％)＞10,从而列出不等式组，再由“饼干的标价是整数元”在不等式组的解集中找出整数解。解略。（答案：饼干的标价为9元，牛奶的标价为1.1元）提炼：列不等式（组）解应用题的关键是寻找不等关系，再由不等关系列出不等式（组），因此要善于挖掘题中隐含的不等关系。Ⅲ.【小结】1．列不等式（组）解实际问题的一般步骤（见填空）2．本节课运用的数学思想方法有数形结合思想、类比思想、转化思想、分类思想等。Ⅳ.【实践】1．教师自行设计作业。复习指导用书第34页第18、19、20题。第9课时函数概念、一次函数溧阳市光华初级中学陈淑峰复习教学目标1、能根据具体问题中的数量关系和变化规律了解函数、一次函数的意义。能说出函数的三种表示方法、一次函数的基本性质，知道函数图象的画法。2、能画简单的一次函数图象，并根据已知条件确定一次函数的表达式。3、能运用类比思想比较函数、一次函数和正比例函数的异同点，初步体会数形结合思想，并能运用数形结合的方法解决有关实际问题，并尝试用函数的方法描述有关实际问题，对变量的变化规律进行初步预测。复习教学过程设计1、【唤醒】一、填空\n（1）写出下列函数中自变量的取值范围。，，。（2）已知与成正比例，且时，，那么与之间的函数关系式为_________________。（3）直线与轴的交点坐标为（_______），与轴的交点坐标为（_______）。（4）根据下列一次函数y=kx+b(k≠0)的草图回答出各图中k、b的符号：二、选择（1）下列函数中，表示一次函数的是()A、B、C、D、（2）已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是()2、【尝试】例1、已知一次函数的图象经过点、，（1）求函数解析式；（2）画出函数图象；（3）函数的图象经过那些象限？（4）当增大时，的值如何？解略（答案：，图略，图象经过一、二、四象限，随增大而减小）例2、已知一次函数（1）当m、n取何值时，y随x的增大而增大？（2）当m、n取何值时，直线与y轴的交点在y轴的下半轴？（3）当m、n取何值时，直线经过一、二、四象限？分析：（1）一次函数的性质：当时，随x的增大而增大；（2）直线与y轴的交点坐标为；（3）当且一次函数的图象经过一、二、四象限。解略（答案：（1），为一切实数；（2）；（3））提炼：利用逆向思维的方法，根据一次函数的性质，体会逆向思维和定向思维的异同。例3、已知：函数y=(m+1)x+2m﹣6（1）若函数图象过（﹣1，2），求此函数的解析式。（2）若函数图象与直线y=2x+5平行，求其函数的解析式。（3）求满足（2）条件的直线与此同时y=﹣3x+1的交点并求这两条直线与y轴所围成的三角形面积。分析：（1）利用函数的表达式与点的坐标的关系；（2）一次函数图象平行，表达式之间的关系；（3）利用点的坐标求线段的长，确定三角形的底和高求三角形的面积。解：（1）由题意:2=﹣(m+1)+2m﹣6\n解得m=9∴y=10x+12(2)由题意，m+1=2解得m=1∴y=2x﹣4(3)由题意得解得:x=1,y=﹣2∴这两直线的交点是（1，﹣2）y=2x﹣4与y轴交于(0,-4)y=﹣3x+1与y轴交于(0,1)∴S△=提炼：利用数形结合的思想方法，根据函数的性质结合图形确定函数的解析式及三角形的面积。例4、如图，l甲、l乙两条直线分别表示甲走路与乙骑车（在同一条路上）行走的路程S与时间t的关系，根据此图，回答下列问题：1）乙出发时，与甲相距10km；2）行走一段时间后，乙的自行车发生故障停下来修理，修车时间为1h；3）乙从出发起，经过2.5h与甲相遇；4）甲的速度为5km/h,乙的速度为15km/h；5）甲行走的路程s(千米)与时间t(小时)之间的函数关系式是s=5t+10(t≥0)；6)在0h2.5h甲走在乙的后面；7)如果乙的自行车不出故障，则乙出发后经过1h与甲相遇,相遇后离乙的出发点15km；在0h1h范围内甲走在乙的后面；并在图中标出其相遇点。(相遇点为A)提炼：运用函数的图象及性质解决实际问题，并对某些实际问题进行比较、预测，体会生活中的数学。3、【小结】（1）本单元知识结构（见唤醒阅读）（2）本节课运用的数学思想方法：类比思想、数形结合思想、猜想。4、【实践】（1）教师自行设计作业。（2）复习指导用书第48页第11题，第53页第12、13题。第10课时反比例函数溧阳市光华初级中学陈波复习教学目标:1.结合具体情景体会反比例函数的意义,能根据已知条件确定反比例函数的表达式.2.会画反比例函数的图象,并能根据图象探索并理解反比例函数的性质,进一步提高从函数图象中获取信息的能力.3.会用反比例函数解决某些实际问题,逐步形成用函数观点处理问题的意识,体验数形结合的思想方法.复习教学过程设计:Ⅰ【唤醒】一、填空1、在式子（1）（2）（3）（4）（5）中哪些是反比例函数\n2、反比例函数（k不为0）的图象既是对称图形，又是对称图形3、函数其图象位于第象限，在其图象所在象限内，y随着x的增大而，当时，y04、函数的图象位于第象限，在其图象所在象限内，y随着x的增大而当x＜0时，y05、反比例函数的图象经过点（2，3），则点（-2，-3）该函数图象上（填“在”或“不在”）二、选择1、如果反比例函数的图象经过点P（-3，2），那么k的值是（）A、6B、C、D、-62、已知P（-6，3）在函数的图象上，那么下列的点不在该函数的图象上的是（）A、（-3，6）B、（，-54）C、（3，-54）D、（-4，）3、若函数的图象位于第一，三象限内，则k的取值范围（）A、k＞3B、k＜3C、k＞0D、k＜04、点（-2，y1）、（-1，y2）、（1，y3）都在反比例函数的图象上，则下列关系式成立的是（）A、y1＞y2＞y3B、y1＜y2＜y3C、y3＞y1＞y2D、y1＞y3＞y25、如图的图象上有三点A、B、C，过三点分别作坐标轴的垂线，分别得到矩形A1AA2O，矩形B1BB2O，矩形C1CC2O，设这三个矩形的面积分别为S1、S2、S3则三者的大小关系（）A、S1＞S2＞S3B、S1＜S2＜S3C、S1=S2=S3D、不能确定Ⅱ【尝试】例题1、已知反比例函数的图象过（1，2），求这个函数的解析式，并画出函数的图象。解略（答案：）例题2、一蓄水池的排水管每小时排水10M3，6h可将满池的水全部排空，如果将排水管每小时的排水量改为Qm3，排空水池的水所需要的时间为th。(1)写出t与Q间的函数关系式，并画出草图。(2)若要将满池的水在4小时内排空，那么每小时的排水量Q至少为多少？(3)如果每小时的排水量为4m3，那么将满池水排空需要多长的时间？\n解略（答案（1）图象位于第一象限（2）Q至少要15m3（3）t=15h）提炼：把实际问题抽象成数学知识，分析变量之间的关系，建立反比例函数模型，解决问题。注意实际问题中变量的取值要符合实际。例题3，反比例函数与一次函数的图象交于A，B两点，（1）求A，B两点的坐标，（2）求三角形AOB的面积（3）当x取何值时，y1>y2分析：将问题转化成求的解，即求出点的横坐标。利用分割法求三角形的面积。（答案A（-2，4）B（4，-2）三角形AOB的面积为6当或时，y1>y2）提炼：利用数形结合的思想，体会图象的交点坐标与一元二次方程的解的关系。例题4、已知反比例函数的图象过（-1，2），直线经过第一，三，四象限，若直线与反比例函数的图象只有一个公共点，求b的值。分析：把点的坐标代入函数表达式求k的值，把问题转化成一元二次方程求有两个相同根的情况，并结合一次函数图象特点求b的值。（答案：）提炼：利用数形结合思想，体会函数图象的交点个数与一元二次方程根的个数的关系。Ⅲ【小结】1、本单元知识结构反比例函数图象和性质反比例函数的应用2、本节课运用的数学思想方法：数形结合思想Ⅳ【实践】1、教师自行设计作业复习指导用书P5819、20第11课二次函数溧阳市光华中学史栋新复习教学目标1．\n根据具体情境分析和建立两个变量之间的二次函数关系，能用表格、表达式、图象表示变量之间的二次函数关系，并能根据具体问题，选取适当的方法表示变量之间的二次函数关系。1．能根据二次函数的表达式确定二次函数的开口方向，对称轴和顶点坐标；会作二次函数的图象，并能根据图象对二次函数的性质进行分析，逐步积累研究函数性质的经验。2．理解一元二次方程与二次函数的关系，并能利用二次函数的图象求一元二次方程的近似根，并能利用二次函数的相关知识解决实际问题。复习教学过程设计Ⅰ.【唤醒】一、填空二次函数的知识结构(阅读)1．函数，当m_____时，该函数是二次函数；当m_____时，该函数是一次函数。2．抛物线y＝2x2＋1的顶点坐标是______，对称轴是，当x＝时，函数取得最___值为；二次函数y＝2x2－8x＋1的顶点坐标是______,对称轴是___________,它的图象是由函数y＝2x2＋1沿着____轴向____平移______个单位，然后再沿着____轴向____平移______个单位得到。二、判断下列函数表达式中哪能些是二次函数（是二次函数打“√”若不是则打“×”）。（1）y＝3x－2()(2)y＝2x2－3x3（）（3）y＝1－2x2()(4)y＝()（5）y＝()(6)()三、选择1．二次函数y＝ax2，当a<0时，y的值恒小于0，则自变量x的取值范围（）。A.x可取一切实数B.x>0C.x<0D.x≠02．抛物线y＝2x2＋x－3与x轴两个交点间的距离为（）。A.2.5B.－0.5C.0.5D.－2.53．有一个二次函数，它的图象经过（1，0）；图象的对称轴是x=2；并且它的顶点与x轴的距离是4，则该函数的表达式是（）A．B.C.D.\nⅡ.【尝试】例1.已知二次函数y＝x2＋bx＋c的图象经过（1，0）与（2，5）两点(1)求这个二次函数的解析式(2)作出该函数的图象，并根据图象回答下列问题：①函数的对称轴、顶点坐标、与x轴的交点坐标②当x取何值时，y>0，当x取何值时，y随x的增大而减小？解略（答案：y＝x2＋2x－3）提炼：用待定系数法求二次函数解析式，用描点法作出图象，根据图象解决二次函数的一些基本性质。例2.函数y＝ax2－ax＋3x＋1的图象与x轴有且只有一个交点，求a的值和交点坐标，求a的值和交点坐标。1．解略（答案：0，（－，0）；1，（－1，0）；9，（，0））提炼：解决函数问题时，先要注意对函数中首项系数a的讨论，然后若有二次函数与x轴交点的关系，则需利用到二次函数与一元二次方程的关系，利用一元二次方程的根的判别式来解决。例3.阅读下面的文字后，解答问题：有这样一道题目：“已知二次函数y＝ax2＋bx＋c的图象经过点A（0，a），B（1，－2），。求证：这个二次函数图象的对称轴是直线x＝2。”题目中的矩形部分是一段被墨水污染了无法辨认的文字。（1）根据现有的信息，你能否求出题目中二次函数的表达式？若能，写出求解过程；若不能，说明理由。（2）请你根据已有的信息，在原题中的矩形框内，填加一个适当的条件，把原题补充完整，并把你所补充的条件填写在原题中的矩形框内。解略（答案：（1）y＝x2－4x＋1，（2）答案不惟一，如填“C（0，1）”或“顶点纵坐标为“－3”等）提炼：学生自己编题，有助于学生加深对题意的理解。另外，解决此类问题，是从题目中的结论到已知条件，有利于训练学生的逆向思维。例4.阅读如下材料，运用材料中的知识解决问题材料：一元二次方程，ax2＋bx＋c＝0(a≠0)有两个实数根x1、x2，根与系数有如下关系：x1＋x2＝－，x1、x2＝，这个关系称为韦达定理。问题：二次函数y＝－x2－(m－3)x＋2(m－1)的图象与x轴交于A，B两点（点A在原点O的左侧，点B在O的右侧），且x1〈x2，也y轴交于点c，线OA与OB的长的乘积等于8，求抛物线的顶点P及点C的坐标。解略（答案：P（－1，9），C（0，8））提炼：应用韦达定理解决二次函数问题，可以将二次函数的问题转化为一元二次方程来解决，体会方程与函数的关系。\nⅢ.【小结】1．本单元知识结构（见填空第1题）。2．本节课运用的数学思想方法：类比思想、数形结合思想、分类思想等。Ⅳ.【实践】1、师自行设计作业。2、复习指导用书P61—63。第13课时平行线、三角形与证明溧阳市第二中学朱淑芳复习教学目标：1、知道补角、余角、对顶角、同位角、内错角、同旁内角的概念，能根据图形或数量关系判断两个角之间的关系，知道三角形三边之间的关系、三角形的内角和定理及三角形的内角、外角、中线、高、角平分线等概念；知道平行线的概念及性质及两直线平行的条件；知道全等三角形的概念、性质及三角形全等的条件；知道角平分线、线段垂直平分线的概念及性质。2、会求一个角的补角、余角，并能利用补角、余角的性质计算或证明；会根据三角形的有关概念计算或证明；会利用平行线的性质计算或证明；会利用全等三角形的概念性质及两个全等三角形全等的条件等解决问题，会利用角平分线及线段垂直平分线的概念、性质解决问题。3、能综合应用所学知识解决问题.复习教学过程设计：一、【唤醒】1、填空：（1）如图，AB∥CD，∠1＝38°，则∠2＝∠3＝∠4＝（2）△ABC中，AB＝3BC＝5，则AC的取值范围是（3）△ABC中，∠A＝30°∠B－∠C＝20°，则∠B＝　　　　∠C＝　　　（4）添加条件，使线段满足题意：①、，AD为△ABC的中线②、，BE为△ABC的高③、，CF为△ABC的角平分线（5）已知，OP平分∠AOB，D为OP上一点，DE⊥OA于E，DF⊥OB于F，OD＝5，DE＝3，则DF＝OF＝P若连接EF，则OD与EF的关系是2、判断（1）若∠A与∠B是同旁内角，则∠A+∠B=180°　　　　　　　　　（　　）（2）若∠α与∠β是互为余角，则∠α+∠β=180°　　　　　　　　（　　）\n（3）若∠1=∠2，则∠1与∠2是对顶角　　　　　　　　　　　　　　（　　）（4）若两个三角形有两条边及一个角对应相等，则这两个三角形全等　（　　）3、选择（1）如图，AB∥DE，∠E=65°，则∠B＋∠C的度数是（）（A）135°（B）115°（C）65°（D）35°（2）如图，D、E分别为△ABC的中点，BC＝8∠A=41°，∠B=48°则下列结论正确的是（）（A）DE=4，∠AED=41°（B）DE=4，∠AED=81°（C）DE=4，∠AED=48°（D）DE=4，∠ADE=48°（3）一个角的补角与它的余角的和比这个角的2倍少30°，则这个角等于（）（A）30°（B）45°（C）60°（D）75°二、【尝试】例1．已知：直线a∥b，A、B为直线a上两点（点A在B的左边），C、D为直线b上两点（点C在点D的左边），AB=CD，画出图形，并连接AD、BC，设交点为O，写出图中所有的全等三角形，并选一对加以证明。分析：首先按题意画出符合要求的图形，由a‖b、AB=CD得到四边形ABCD为平行四边形，然后根据平行线的性质得到相等的角，再根据三角形全等的条件得到答案。解略（答案：△ABD≌△DCA△ABC≌△DCB△AOB≌△DOC△AOC≌△DOB）提炼：本题考查平行线的性质及三角形全等的条件，并且涉及读句画图等知识。例2．例1中，若其他条件不变，把“AB=CD”该为“AC=BD”，则上述所得结论都还一定成立吗？写出仍能成立的，若有不能成立的，画图说明。分析：先按题意画出符合要求的图形，并考虑情况的多样性，进一步应用三角形全等的条件。解略（答案：△ABD≌△DCA、△ABC≌△DCB、△AOC≌△DOB，其中△AOB≌△DOC不一定成立）提炼：本题主要说明“SSA”不能说明三角形全等，同时考虑情况的多样性。例3．如图，△ABC，△EDC都是等腰直角三角形，且点C在AD上，AE的延长线与BD交于点F，请在图中找出一对全等三角形，并写出证明全等的过程。分析：由等腰直角三角形的定义可得AC=BC，DC=EC，再由∠ACB=∠DCE可得△ACE≌△BCD证明略提炼：本题考查等腰三角形的定义及三角形全等的条件，也考查学生在复杂问题中寻找所需图形的能力\n例4．如图，AB=AE，∠ABC=∠AED，BC=ED，点F是CD的中点。（1）求证：AF⊥CD（2）在你结论证明完毕后，还能得出什么新结论，请写出三个（不要证明）分析：连接AC、AD，AB=AE，∠ABC=∠ADEBC=ED得△ABC≌△AED，得AC=AD，又F是CD的中点，所以AF⊥CD。证明略提炼：本题考查学生由已知条件构造三角形，用三角形全等的条件得全等三角形，并考查等腰三角形的性质。三、【小结】：本节课主要复习了角与角在大小和位置上的关系，并复习了平行线的性质和条件，同时也复习了三角形全等的条件和性质，并能综合应用。四、【实践】：1．教师自行设计2．复习指导P77、12P79、6、8、10、13第14课时特殊三角形溧阳市第二中学彭云复习教学目标:1、知道等腰三角形和等边三角形的性质和判定；了解直角三角形的概念；知道直角三角形的性质和判定直角三角形的条件;能说出线段中垂线的性质.2、会用等腰三角形的性质和判定进行有关的计算和证明；会用直角三角形的性质进行简单计算；能写出一个命题的逆命题;会用勾股定理解决简单计算，并会用它的逆定理判定直角三角形；会用“HL”定理判定直角三角形全等。3、能用分类讨论的思想解决等腰三角形中的有关计算、用转化的思想将不规则图形转化为规则图形.复习教学过程设计Ⅰ、【唤醒】一、填空性质:两腰相等、等边对等角、等腰三角形判定+等边三角形性质特殊三角形判定性质直角三角形判定含30角的直角三角形的性质：等腰直角三角形直角三角形全等的特殊判定方法是：线段垂直平分线的性质:二、判断：1、两底角相等的三角形是等腰三角形.()2、等腰三角形一定不是钝角三角形.()3、等腰三角形中，有一个角是50°，那么它的底角必是65°.()4、等腰直角三角形底边上的高等于底边的一半.()\n5、如果原命题是假命题,那么它的逆命题一定是假命题.()6、有两边对应相等的直角三角形是全等三角形.()三、选择:1、等腰三角形的一边长是10cm，另一边长是6cm，则它的周长是（）A、26cmB、22cmC、16cmD、22cm或26cm2、已知一个直角三角形的两边长分别是3和4，则第三边的长是（）A、4B、5C、D、5或3、如图，在Rt△ABC中，斜边AB的垂直平分线分别交AB、AC于点E、D，∠A=15°，若AD=4，则BC=（）A、4B、2C、1D、4、等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为()A、75°或15°B、30°或60°C、75°D、30°5、直角三角形斜边上的中线和面积分别是5cm，20cm2，则它的斜边上的高是（）A、3cmB、4cmC、5cmD、2Ⅱ、【尝试】例1:已知，在△ABC中，AB=AC，点M，N在BC上，且AM=AN，请你用最简便的方法说明BM=CN。分析：作底边上的高，灵活运用“三线合一”性质证明：略提炼：究竟作角平分线还是作高或中线，要依具体问题。例2、已知:如图,在△ABC中,D是BC边上的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求证:AB=AC(提示:先用“HL”证△BDE≌△DFC,然后运用“等角对等边”得证)证明：略提炼:在直角三角形中会灵活运用“HL”定理例3:如图，已知在△ABC中，AD、CE是高，且AE=3，BE=2，CE=4，在不添加任何辅助线和字母的条件下，你能得到哪些正确结论？（分别从边、角、三角形相似三个角度去思考）分析：首先从高和一些线段的长的角度去思考，由直角三角形中的边联想到运用勾股定理求出AC、AD、BC、DE，然后利用等腰三角形、直角三角形，三角形相似等有关知识逐步得到结论。解：①AB=AC，②BD=CD=DE，③AD=BC，④∠ABC=∠ACB=∠BED，⑤∠BDE∠=BAC，⑥∠BAD=∠CAD=∠BCE=∠CED，⑦∠ACE=∠ADE，⑧∠ACD+∠AED=180°，∠BAC+∠CDE=180°，⑨△BAD≌△CAD，⑩△BAD∽△BCE，⑾△CAD∽△BCE，⑿△BDE∽△BAC提炼：注意仔细分析已知条件，思考哪些已知条件组合在一起可以产生新的结论及可能产生的新的结论。例4:如图，在四边形ABCD中，AB=AD=4，∠A=60°，∠D=150°,CB⊥AB，已知四边形ABCD的周长为16，求S四边形ABCD分析：不规则图形往往转化为规则图形，若连接BD后，由AB=AD=4，\n∠A=60°容易判断△BAD是等边三角形，并且得到△BDC是含30°角的直角三角形，那么S四边形ABCD=S△ABD+S△CBD，根据已知条件可算到CD+BC=8，然后根据2CD=BC可求出CD,BC。解：连接BD，则△BAD为等边三角形，∴AD=BD=4，∠ADB=60°，CD+BC=8又∠ADC=150°，∴∠BDC=90°,∠DBC=30°在Rt△BDC中可求得CD=,BC=,BD=BC*cos30°=∴S四边形ABCD=S△ABD+S△CBD=×4×2＋×4×=4+=提炼：运用“转化”的数学思想将不规则图形转化为规则图形，注意在等边三角形和直角三角形中运用其性质灵活求解三角形的边长。变式:在四边形ABCD中，AB=AD=4，∠A=60°，∠D=150°,四边形ABCD的周长为16，又该如何求S四边形ABCD?分析:注意在直角三角形中常用勾股定理建立方程求边长。如:设CD=x，则BC=16-4-4-x=8-x在BDC中，有BC2=BD2+DC2，即（8-x）2=x2+42，解得x=3。∴CD=3,BC=5.(略)Ⅲ、【小结】1、本节课主要内容：见唤醒中的“知识结构图”。2、分类讨论的思想、（如：在等腰三角形中，若已知一个角求另外两个角或已知一边求另外两边，通常要分类讨论）、数形结合的思想，转化的思想等。Ⅳ、【实践】（1）教师自行设计作业；（2）复习指导用书第83--86页第1、3、4、9、13、14、19、22、25、26题。第15课时多边形、平行四边形和证明溧阳市第二中学彭云复习教学目标:1、能说出多边形的内角和定理和外角和定理；知道平行四边形的性质和判断；2、会求多边形的内角和，并能判定一个多边形是几边形；会进行有关平行四边形的边角的简单计算；能运用性质和判定进行相关的证明；能识别中心对称图形。3、能用数形结合的思想解决平行四边形中的计算和证明。复习教学过程设计Ⅰ、【唤醒】一、填空内角和定理：n边形的内角和等于1、多边形的有关性质外角和定理：n边形的外角和等于对角线：n边形的对角线共有条性质：包括边、角、对角线、对称性等判定多边形①两组对边分别平行---_____2、四边形②一组对边平行且相等----略3、其它多边形二、判断：\n1、四边形具有平行四边形所有的性质.()2、平行四边形的对角线互相平分且相等.()3、平行四边形既是轴对称图形又是中心对称图形.()4、一组对边平行,另一组对边相等的四边形是平行四边形.()5、一组对边平行,一组对角相等的四边形是平行四边形.()6、平行四边形的两条对角线把平行四边形分成四个面积相等的小三角形.()7、正八边形和正方形的组合能够进行密铺.()三、选择:1、ABCD的四个内角的度数的比∠A:∠B:∠C:∠D可能是()A、2:5:2:5B、3:4:4:3C、4:4:3:2D、2:3:5:62、下列图形是中心对称图形的是()AB、C、D、3、若一个多边形的每一个内角都等于120°，则它是()A、正方形B、正五边形C、正六边形D、正八边形4、如图，在ABCD中，AE平分∠DAB，∠B=100°，则∠DEA=()A、100°B、80°C、60°D、40°5、下列图形中,不能进行密铺的是()A、正三角形B、正方形C、正六边形D、正五边形6、如图，在ABCD中，EF过对角线的交点O，交AD于E，交BC于F，已知AB=4，BC=5，OE=1.5,则四边形EFCD的周长是()A、14B、12C、16D、10Ⅱ、【尝试】例1:如图,ABCD的对角线AC,BD相交于点O,由此你能得出哪些结论?试尽可能多的写出一些来.分析:分别从平行四边形的边、角、对角线方面去考虑，然后思考从这些结论出发得出的新的结论。解：AB=CD，AD=BC，DO=BO，AO=CO，∠ADC=∠ABC，∠DAB=∠DCB，∠ADB=∠DBC，∠BDC=∠ABD，∠DCA=∠CAB，∠ACB=∠DAC△ADO≌△CBO，△DOC≌△BOA，△ADC≌△CBA，△ADB≌△CBD，S△DOC=S△AOD=S△AOB=S△BOC等。提炼:对于这种结论开放的题目，要注意思维发散，灵活运用平行四边形的性质，从不同的角度去考虑。例2：图,已知一个多边形的内角和是它的外角和的5倍，求这个多边形的边数。分析：注意多边形的外角和始终是360°解：设这个多边形是n边形，则(n-2)×180°=5×360°,得n=12\n答：这个多边形是十二边形。提炼：多边形的内角和与外角和既有区别，又有联系。多边形的内角和随边数的变化而变化，而外角和是一个定值。已知内角和与外角和的关系，可以运用方程思想解决。例3:如图:在△ABC中,D、E分别是AB、AC的中点，F是DE延长线上的点，且EF=DE，则图中的平行四边形有哪些？说说你的理由。分析：已知条件中AE=EC，DE=FE，不难得到四边形ADCF是平行四边形，然后推出AD∥CF，又可证到AD=CF，所以四边形DBCF也是平行四边形。解：ADCF，DBCF理由：∵D、E分别是AB、AC的中点∴AE=EC，AD=DB，又∵EF=DE，∴四边形ADCF是平行四边形（对角线互相平分的四边形是平行四边形）∴AB∥CF，AD=CF，∴BD=CF，∴四边形DBCF也是平行四边形（一组对边平行且相等的四边形是平行四边形）提炼：运用数形结合的思想，灵活运用平行四边形的判定方法，关注由结论又可以推出新的结论。例4:如图,已知ABCD的周长为40,高AE=6,高AF=9,试根据条件设计一个问题,并进行解答.分析：答案不唯一，如：已知ABCD的周长和边上的高，会想到平行四边形的面积，而平行四边形的面积要涉及底和高，所以可以设计求平行四边形的边长。解：设计的问题可以是：求AB、BC的长。因为ABCD的面积S=BC*AE=CD*AF所以6BC=9CD，因此BC=CD，又因为ABCD的周长为40，所以BC+CD=20，可解得AB=8，BC=12提炼：运用数形结合的思想，将已知条件和图形结合起来考虑。Ⅲ、【小结】1、本节课主要内容：见唤醒中的“知识结构图”。2、运用数形结合的思想、方程的思想解决平行四边形中的计算和证明。Ⅳ、【实践】（1）教师自行设计作业；（2）复习指导用书第88--90页第1、4、5、7、8、10、11、13、15、16、17题。第16课时特殊平行四边形、梯形与证明溧阳市第二中学钱惠琴复习教学目标：1、能说出矩形、菱形、正方形、梯形的概念和性质，以及四边形是矩形、菱形、正方形、等腰梯形的条件，了解它们之间的关系。知道直角三角形斜边上的中线等于斜边的一半。2、会根据矩形、菱形、正方形、梯形的性质和判定进行运算和推理，理解顺次连接一个四边形的中点所构造的四边形是特殊的四边形。3、能运用转化思想将梯形转化为平行四边形和三角形问题解决，并能运用类比、逆向联想及运动的思维方法来研究问题。\n复习教学过程设计：Ⅰ.【唤醒】一、填空：1、请同学们仿照图中已填写的部分将它们补充完整：2、对角线_____________的平行四边形是菱形。3、对角线_____________的四边形是矩形。4、直角三角形斜边上的中线等于_____________。5、正方形具有而矩形不具有的性质是________________。6、请写出等腰梯形ABCD(AB∥CD)具有而一般梯形不具有的三个特征:__________________，__________________，______________________。7、顺次连接矩形的四边中点所得的四边形是_____________形。二、判断：1、角线互相垂直的四边形是菱形（）4、腰梯形的两个底角相等（）2、个角都相等的四边形是矩形（）5、组对边平行的四边形是梯形（）3、角线互相垂直且相等的四边形是正方形（）三、选择：1、菱形的一个内角是120º，一边长是8，那么它较短的对角线长是（）A．3B．4C．8D．82、梯形的上底长为6cm，过上底一个顶点引一腰的平行线，交下底所得的三角形的周长是19cm，那么这个梯形的周长为（）A．31cmB．25cmC．19cmD．28cm3、若矩形一内角的平分线分长边为两部分的长分别为2和3，则该矩形的面积为（）A．6B．10C．15D．10或154、如图，四边形ABCD是正方形，四边形AEFC是菱形，则∠FAB等于（）A．45ºB．30ºC．75ºD．22.5º5、下列各组图形中，既是轴对称图形，又是中心对称图形的是（）A．平行四边形、菱形、正方形B．等腰梯形、矩形、正方形C．等边三角形、矩形、圆D．菱形、正方形、圆Ⅱ.【尝试】例1、如图，把一张矩形纸片ABCD沿BD对折，使点C落在E处，BE与AD相交于O，写出一组相等的线段______________________________(不包括AB=CD,AD=BC)分析:本题是开放性问题,答案不唯一,可采用两种方法:(1)从条件入手,根椐对称性质、全等性质、矩形的性质等，逐步深入分析，发现需要的结论；(2)通过观察、比较找出可能相等的线段，再论证。解：BE=BC或CD=ED或AB=ED或OB=OD或OA=OE。\n提炼：折叠的问题实质就是对称的问题，在折叠的问题中折痕所在的直线就是对称轴。在折痕两侧互相重合的部分是全等的图形，从而可以得到许多相等的边、角。例2、如图，ABCD的对角线AC的垂直平分线与AD、BC分别交于E、F，求证：四边形AFCE是菱形分析:由于四边形AFCE的对角线互相垂直，那么只需证明对角线互相平分即可，故只需证OE=OF，而这可由证明△AOE≌△COF得到。证：（略）提炼：解决此题的关键是要准确理解题意，EF是线段AC的垂直平分线。另一种方法证完后还可问学生，还有其他方法吗？注重一题多解，激活学生的思维。例3、如图，两个四边形中，∠ADB=∠ACB=90º，E、F分别是DC、AB的中点。(1)观察两个图形，你发现了什么？在下面横线上简要写出你的发现(2)试猜想EF与DC在位置上有无特殊关系？如有，请证明；如没有，请说明理由。分析：（1）认真审题，注意图形位置的变化；（2）由直角三角形斜边上的中线等于斜边的一半可知，连结FC、FD，可得FC=1/2AB=FD，又已知CE=DE，根据等腰三角形的三线合一可得EF垂直CD。略解：（1）图（2）中Rt△ACB由图（1）中Rt△ACB沿AB翻折180º而得到。（2）EF是CD的中垂线。理由略。提炼：要能体会知识之间的内在联系，合理添加辅助线，化难为易。例4、已知直角梯形ABCD中，AD∥BC，AB⊥BC，AB=6，AD=8，∠C=45º，有一点P从D向A以每秒1个单位的速度行动，有一点Q从B向C以每秒1.5个单位的速度行动。问：在运动过程中四边形PQCD能成为特殊的四边形吗？什么时候成为怎样特殊的四边形？分析：由于AD∥BC，四边形PQCD能否成为特殊的四边形，只需看点P、点Q在运动过程中四边形PQCD的对边或邻边能否相等，因此需分情况讨论并计算。解略（当t=5.6秒时，四边形PQCD为平行四边形；当t=0.8秒时，四边形PQCD为等腰梯形；当t=3.2秒时，四边形PQCD为直角梯形。）提炼：要注意数形结合和分类思想，同时考虑问题要全面，防止遗漏。Ⅲ、【小结】：1、单元知识结构（见填空），并重点从边、角、对角线理解特殊平行四边形、梯形的性质和判定。2、本课运用的数学思想方法：转化思想、类比思想、分类思想等。Ⅳ、【实践】1、教师自行设计作业。2、复习指导用书第92——94页练习五、第96——97页练习六。第17课时圆（1）溧阳市第二中学张云娟复习教学目标：1、知道圆、弧、弦、圆心角、圆周角等基本概念；认识圆的对称性；了解圆锥的侧面展开图是扇形。2、\n能用垂径定理，圆心角、弧、弦之间关系定理，圆周角定理及推论，弧长公式等进行简单的运算和推理；会通过作图的方法理解确定圆的条件。1、会用折叠、旋转、圆的对称性及分类讨论的思想方法探索图形的有关性质，能将有关弦长、半径的实际计算问题转化成解直角三角形问题解决。复习过程设计一、【唤醒】1、填空基本概念：弧、弦、圆心角、圆周角确定圆的条件：对称性：垂径定理及逆定理圆基本性质：圆心角、弧、弦的关系定理：圆周角定理：同弧或等弧所对的圆心角是它所对的圆周角的推论：（1）同弧或等弧所的圆周角（2）90°的圆周角所对弦是，与圆有关的计算公式：（1）；（2）；（3）；(4)；2、判断：（1）圆是轴对称图形，其对称轴是任意一条直径；（）（2）平分弦的直径垂直于弦，并且平分弦所对的弧；（）（3）过任意三点可确定一个圆；（）（4）任何三角形只有一个外接圆，一个圆也只有一个内接三角形；（）（5）一条弦所对的圆心角是它所对的圆周角的2倍。（）3、选择题：（1）⊙O的直径为10，圆心O到弦AB的中点M的长为3，则弦AB的长是（）（A）4；（B）6；（C）7；（D）8（2）△ABC内接于⊙O，AB=AC，∠A=50°，D是⊙O上一点，则∠ADB的度数为（）（A）50°；（B）65°；（C）65°或50°；（D）115°或65°（3）如图所示，⊙A、⊙B、⊙C、⊙D、⊙E相互外离，它们的半径都是1，顺次连接五个圆心，得到五边形ABCDE，则图中五个扇形（阴影部分）的面积之和是（）（A）∏；（B）1.5∏;（C）2∏;（D）2.5∏(4)如果圆锥的侧面展开图的面积是15∏cm2,母线长是5cm，那么圆锥的底面半径为（）（A）3cm；（B）1.5cm；（C）6cm；（D）4cm(5)已知△ABC是半径为2的圆内接三角形,若BC=2，则∠A的度数为（）（A）30°；（B）60°；（C）120°；（D）60°或120°（6）图中的五个半圆，邻近的两个半圆相切，两只小虫同时出发，以相同的速度从A点到B点甲虫沿弧ADA1、弧A1EA2、弧A2FA3、弧A3GB的路线爬行，乙虫沿弧ACB的路线爬行，则下列结论正确的是（）（A）甲虫先到B点；（B）乙虫先到B点；\n（C）甲虫、乙虫同时到达B点；（D）无法确定。二、【尝试】例1、如图，在△ABC中,∠BAC的平分线AD交△ABC的外接圆⊙O于点D,交BC于点G,若AG=6,DG=2,求CD的长。分析：连接DC，用相似三角形解决。解略。（DC=4）例2、ABC中，AB=AC=10，BC=12，求△ABC外接圆的半径。分析：利用三角形外心的特殊位位置和垂径定理构造直角三角形解决。解略。（△ABC外接圆的半径为6.25）。提炼：善于用数学转化的思想方法，将不同情境下的数学问题转化为比较熟悉的直角三角形问题解决。例3、1）如图，小军学完垂径定理,逆向思考得出一个结论：“弦的垂直平分线一定经过圆心，并且平分弦所对的两条弧”，你认为小军的猜测正确吗？为什么？（2）你能用上面的结论，帮助考古学家用尺规作图的方法确定古圆盘的半径吗？分析：（1）根据圆上的点到圆心的距离相等进行说理（2）圆心可有两条不同的直径相交确定，因此要确定圆心，只要确定出两条不同的直径就可，由两条不同的弦，作其垂直平分线，则交点就是圆心。解：（1）∵圆心O到A和B的距离相等，∴点O一定在AB中垂线上。即AB的中垂线过圆心。（2）略提炼：能将学圆性质时的探究方法灵活运用到探索新的有关结论，并能应用。例4、※如图：把直角三角形ABC的斜边AB放在直线l上，按顺时针方向在l上转动两次，使它转到△A2B2C2的位置，设BC=1，AC=，则点A运动到点A2的位置时，点A经过的路线长是多少？点A经过的路线与直线l所围成的面积是多少？分析：点A经过的路线长就是以B为圆心，以AB为半径的圆弧和以C2为圆心，以AC为半径的圆弧的长度。面积就是两个扇形面积与一个直角三角形的面积和。解：点A经过的路线长为π；点A经过的路线与直线l所围成的面积是π+\n提炼：在理解旋转性质的基础上将问题转化为所学的有关圆的计算公式解决。三、【小结】1、知识结构：见上表2、基本数学思想方法：转化的思想；分类讨论的思想；数形结合的思想等。3、解题注意点：（1）在解决问题的过程中，注意归纳总结出解决问题的一些基本规律，提高学习效率；（2）注意解决问题的严密性，充分考虑各种情况。四、【实践】教师自行设计作业；复习指导用书第107～109页第1、2、5、6、9、12、21题。第18课时圆（2）溧阳市第二中学张云娟复习教学目标：1、知道圆与点、圆与直线、圆与圆的不同位置关系；知道切线的概念。2、会用圆心到点的距离大小判断圆与点的位置情况，圆心到直线的距离大小判断圆与点直线的位置情况；圆心到圆心的距离大小判断圆与圆的位置情况；会用圆的切线的判定定理和性质定理及两圆相切的性质与判定进行简单的推理与计算；会作三角形的外接圆、内切圆，会过圆上点作圆的切线。3、能从运动的观点与分类讨论的思想方法探索图形之间的关系和有关性质。复习过程设计一、【唤醒】1、填空（1）点在圆外点到圆心的距离d>r圆与点的位置关系：（2）点到圆心的距离dr（3）点到圆心的距离dr（1）相离圆心到直线的距离d>r圆与直线的位置关系（2）圆心到直线的距离dr圆（3）圆心到直线的距离dr（1）相离圆与圆的位置关系：（2）相交（3）相切2、判断：（1）若圆经过A、B两点，则圆心一定可能是线段AB的中点；（）（2）若直线与圆有公共点，则直线与圆相交；（）（3）圆的切线垂直于圆的直径；（）（4）垂直于直径的直线是圆的切线；（）（5）垂直于圆的切线的直线一定过切点；（）（6）若两圆无公共点，则这两圆外离；（）（7）直线l上一点P到圆心O的距离等于半径R，则直线l与圆O相切。（）3、选择题：（1）A、B两点到点O的距离等于4cm，则点A、B在（）（A）⊙O上；（B）⊙O内；（C）⊙O外；（D）无法确定。\n（2）如图所示：已知等边△ABC的边长为2cm，下列以A为圆心的各圆中，半径是3cm的圆是（）（A）；（B）；（C）；（D）（3）点P到△ABC各边的距离相等，则点P是△ABC的（）（A）内心；（B）1.外心;（C）中心;（D）垂心。(4)已知△ABC的三边分别是6、8、10，则此三角形外接圆的半径为（）（A）10；（B）6；（C）4；（D）5(5)两个同心圆，大圆的弦AB与小圆相交于点C、D两点，若AB=6，CD=2，则两圆组成的圆环面积是（）（A）32π（B）16π（C）8π；（D）无法确定二、【尝试】例1、已知Rt△ABC的斜边AB=13，AC=5，CD是AB边上的高。（1）以C为圆心，当半径为多少时，AB与⊙C相切？（2）此时⊙C与点A、B、C、D之间是怎样的位置关系？分析：判断点与圆的位置关系关键是利用圆心到点的距离与半径的大小关系；判断直线与圆的位置关系关键是利用圆心到直线的距离与半径的大小关系，而不是直线上任意一点到圆心的距离。解略。（答案：R=60/13；点A、B在圆外，点D在圆上，点C在圆内。）提炼：让学生通过具体问题的解决进一步体会分类思想是研究图形的一种。重要的数学方法。例2、已知，如图AB=8，AC=6，以AC和BC为直径作半圆，过AB的延长线上一点D作直线，分别与⊙O1和⊙O2相切于点M、N，求BD的长。分析：正确理解圆的切线的性质定理，由切线想过切点作半径，可得到垂线段，然后利用三角形相似求得线段BD的长。解略。（答案：BD=1）提炼：能利用方程的思想，根据切线的性质结合相似三角形的知识，通过设未知数列方程加以计算。例3、读句画图：⊙O和任意一点P，连接OP，以OP为直径作⊙Q。（1）、在所画的图形中，⊙O与⊙Q有怎样的位置关系？\n（2）、当⊙O与⊙Q相交时，交点为A、B，分别作直线PA与PB，则PA、PB与⊙O是什么位置关系？并说明理由。（3）、在题（2）下，连接AB、OA、OB，请根据所画图形尽可能多地写出你认为正确的结论。分析：①画图时要能想到点P与⊙O的不同位置，从而⊙O与⊙Q也就有不同的位置情况。②利用切线的判别定理说明直线与圆的位置关系。③正确画图的基础上，寻找线段之间、三角形之间的数量与位置关系。解：①两圆有内切、相交、内含这三种位置关系；②直线PA与PB是⊙O的切线；③在一般情况下，线段OQ垂直平分AB，在特殊情况下，除了具有一般情况下的结论，线段OQ与AB互相垂直平分。提炼：在画图时通常需要分类讨论，并且用特殊到一般的思想方法解决具体问题三、【小结】1、知识结构：见上表2、基本数学思想方法：转化的思想；分类讨论的思想；由特殊到一般的思想等。3、解题注意点：在解决问题的过程中，注意解决问题的严密性，充分考虑各种情况。四、【实践】（1）教师自行设计作业；（2）复习指导用书第107～109页第3、4、16、18、22题。第19课时作(画)图溧阳市第二中学朱淑芳复习教学目标:1、能用三角板或量角器过一点画已知直线的垂线,能用三角板、直尺过直线外一点作已知直线的平行线；能用直尺和圆规作一条线段等于已知线段、作一个角等于已知角；作角的平分线；作线段的垂直平分线。了解尺规作图的步骤，对于尺规作图题会写已知、求作和作法（不写证明）；2、会用三角板作三角形的高，会用直尺和圆规利用已知条件作一个三角形；会过一点、两点和不在一条直线上的三点作圆；3、把一些较复杂的作图问题转化为基本作图问题来解决。复习教学过程设计：一、【唤醒】1、填空：（1）尺规作图的基本工具是和。作一条线段等于已知线段作一个角等于已知角（2）（阅读）基本作图：作一个角的角平分线作一条线段的垂直平分线已知三边作三角形已知两边及夹角作三角形（3）（阅读）利用基本作图作图已知两角及其夹边作三角形已知底边及底边上的高作等腰三角形过一点、两点和不在一条直线上的三点作圆。\n1、判断：（1）画一条直线a，使a=10cm。（）（2）过点A作线段BC的中垂线。（）（3）过三点A、B、C一定能画一个圆。（）（4）过一点一定能作一条已知直线的垂线。（）2、选择：（1）三角形的外心是（）A、三条高的交点B、三条中线的交点C、三条角平分线的交点D、三边垂直平分线的交点（2）到B、C两点的距离相等的点有（）A、一个B、两个C、无限个D、有限个（3）下列所给条件不能确定一个圆的是（）A、圆心及圆经过的一点B、圆心及半径C、圆经过的两点D、一段圆弧二、【尝试】例1利用尺规，按下列要求作图，不写作法，保留作图痕迹。（1）作出AB的中点M；（2）作∠BCD的平分线；（3）延长CD到P，使DP=2CD。分析：本题考查学生用尺规进行基本作图解：（略）提炼：本题同时考查了尺规作垂直平分线、作角平分线、作一条线段等于已知线段等知识。例2小明的爸爸上街配一块三角形的玻璃，到街上后发现把所量的三边长度弄丢了，打电话问小明，小明却回答他：两边长为30cm和50cm，这两边的夹角为45。请问：按照这三个数据，他爸爸能配到符合要求的玻璃吗？若能，请按1：10的比例画出这个三角形；若不能，请说明理由。分析：根据“两边及夹角对应相等的三角形全等”，所以能配到符合要求的玻璃。解：（略）提炼：这题一方面考查了三角形全等的判定，另一方面帮学生复习1：10作图的含义。例3已知Rt△ABC中，∠C=，用直尺和圆规作图，把它分成两个直角三角形，且要求其中至少一个三角形为等腰三角形（至少两种方法）分析：本题关键是根据等腰三角形的定义想办法得到相等的线段解：（略）提炼：本题是开放题，考查基本作图方法及一些知识的综合运用。\n例1两条公路a、b相交于点O，A、B为两个收购站，请在这块地上找一个仓库P，使仓库到两个收购站的距离相等。分析：到两点A、B的距离相等的点在线段AB的垂直平分线上，到两边的距离相等的点在交角的平分线上，所以求交点即可。解：（略）提炼：本题通过分析题意，运用作垂直平分线和作角平分线找交点，体现数学与生活的联系。三、【小结】前面填空部分，并能用所学综合知识解决实际问题。四、【实践】1、教师自行设计；2、复习指导：P112:3、5、6第20课时视图溧阳市第二中学王飞浦春萍复习教学目标：1、认识点、线、面，会说出它们之间的关系；认识圆柱、圆锥、棱柱、球，会结合点线面说出它们的特征；知道圆柱、圆锥的侧面展开图、正方体的侧面展开图，认识正方体、圆柱、圆锥的截面形状，知道物体的三种视图；认识多边形。2、会识别简单物体的三视图，会根据三种视图描述基本几何体或实物原型；会画立方体极其简单组合体、圆柱、圆锥、球、直三棱柱、直四棱柱的三种视图。3、能由实物形状想象出几何图形，由几何图形想象出实物形状，进行几何体与其三视图、展开图之间的相互转化。复习教学过程设计：（阅读）生活中的立体图形一、【唤醒】1、填空：（1）*在画视图时，看得见部分的轮廓线通常画成实线，看不见部分的轮廓线通常画成虚线。（2）点动成，线动成，面动成。（3）四棱柱（或n棱柱）有棱，个顶点，个面，这些面的形状都是。\n（4）圆柱的侧面展开图是，截面可能是；圆锥的侧面展开图是，截面可能是。(5)写出三视图中有一个是三角形的两个几何体：。2、判断：（1）如图，正三棱柱的主视图、左视图、俯视图分别是：（）（2）一空间几何体的三视图如图所示，则这个几何体是圆柱。（）（3）如图，截一个正方体得到的截面形状是平行四边形。（）3、选择：（1）图中几何体的左视图是（）（2）在下图中，平面图形经过折叠不能围成正方体的是（）（3）如果从一个多边形的某个顶点出发，与其余不相邻的各个顶点连接，能得到2002个三角形，那么这个多边形的边数为（）A、2001B、2002C、2003D、2004（4）俯视图是的几何体是（）（5）将下图所示放置的Rt△ABC（∠C=90）绕斜边AB旋转一周所得到的几何体的主视图是下面四个图形中的（）（6）如图所示的玩具是由两个正方体用胶水黏合而成的，它们的棱长分别为1分米和2分米。为了美观，现在其表面喷涂油漆，已知喷涂1平方分米需用油漆5克，那么喷涂这个玩具共需油漆（）A、120克B、130克C、140克D、150克（7）小丽制作了一个如图所示的正方体礼品盒，那么这个正方体的平面展开图可能是（）（8）图示是由一些相同的小正方体构成的立体图形的三视图，构成这个立体图形的小正方体的个数是（）A、5B、6C、7D、8二、【尝试】\n例1画出下列几何体的三种视图。答案：例2如图的几何体是在正方体的中心挖去一个圆柱得到的，试画出该几何体的三视图。分析：这是一个正方体和圆柱的简单结合体，可先分别考虑它们的三视图，而后结合该几何体的特征思考它三视图中实线、虚线的画法。答案：例3下图的四边形是一个四棱柱的俯视图，尝试画出它的主视图和左视图。分析：根据棱柱的定义，该几何体的侧面形状都是长方形，可以由其俯视图想象出几何体形状，再思考其三视图的画法，并注意画三视图的相关要求。答案：提炼：以上三题都考查了学生对几何体与其三视图之间的相互转化能力。例4用若干个小立方块搭成一个几何体，它的主视图和俯视图如图所示：（1）俯视图上标注A、B的各由几个小立方块搭成？（2）搭成符合上述要求的几何体，至少需要多少个立方块？最多需要多少个立方块？（3）这样的几何体共有几种？画出两种不同的左视图。分析：由主视图易知，A、B上各由3个、1个小立方块搭成，关键分析中间一列的小立方块数，每个位置上最多2个，最少1个立方块且至少有一个位置上有2个小立方块，分情况讨论后，这样的几何体共计有4种。答案：（1）3个，1个；①②③④（2）至少8个，至多10个；（3）4种。左视图：提炼：该题实现了“视图—几何体—视图”的转化过程，可列举各种情况后再得到各种左视图。三、【小结】1、见前面知识结构图；2、由实物形状想象出几何图形，由几何图形想象出实物形状，进行几何体与其三视图、展开图之间的相互转化。四、【实践】1、教师自行设计作业；2、复习指导用书第122页第1~5、7、8、10、11题。第21课时投影溧阳市第二中学钱惠琴复习教学目标：1、通过实例了解平行投影和中心投影的含义，了解视点、视线和盲区的含义。2、会确定物体在太阳光和灯光下的影子，初步进行平行投影和中心投影条件下物体与其投影之间的相互转化。能体会视点、视线和盲区在生活中的应用，并能在简单的平面图和立体图中表示。3、能根据在太阳光下同一时刻物体与影长成正比或相似三角形来帮助我们解决一些实际问题，会用“数学的眼光”看世界，体会数学与现实生活的联系。\n复习教学过程设计：Ⅰ.【唤醒】一、填空1、物体在光线的照射下，会在地面或墙壁上留下它的，这就是投影现象。2、太阳光线可以看成光线，像这样的光线所形成的投影称为；探照灯、手电筒、路灯等的光线可以看成是从点发出的，像这样的光线所形成的投影称为。3、请你各举一个平行投影和中心投影的实例：。4、当人观察物体时，眼睛的位置称为，由视点发出的线称为，看不到的地方称为。5、从远处走近一个物体，我们会感觉这个物体越来越大，这是因为。二、判断：1、你见过的皮影或自己用手势做的手影都是在太阳光照射下形成的中心投影。（）2、两人在太阳光下行走，同一时刻他们的身高与其影长的比相等。（）3、如果一根木杆在太阳光下的影长等于木杆的长，那么这根木杆与地面平行。（）4、较大的会场都成阶梯形状是为了缩小各座位的盲区。（）5、物体的主视图实际上就是该物体在某一时刻某一光线下的投影。（）三、选择：1、在同一时刻，物高与影长成正比例，如果高为1.5米的测竿的影长为2.5米,那么影长为30米的旗杆的高是()A．20米B．18米C．16米D．15米２、已知下面的四幅图是小红某天四个时刻看到的一根木棒及其影子的情况，那么她看到的先后顺序是　　　　（）（1）（2）（3）（4）A．（1）（2）（3）（4）Ｂ．（2）（1）（3）（4）Ｃ．（4）（3）（1）（2）Ｄ．（4）（1）（3）（2）3、如图，晚上小亮在路灯下散步，小亮由A处走到B处这一过程中，他在地上的影子（）A．逐渐变短　B．逐渐变长C．先变短后变长D．先变长后变短4、兄弟两人在家中向窗外观察，图中虚线表示视线，则（）（A．哥哥的盲区大B．弟弟的盲区大Ｃ．两人的盲区一样大　　　　　　　Ｄ．盲区大小不确定5、乘车沿着平坦大道向前行驶时发现前方高一些的建筑物“沉”到位于它们前面的矮一些建筑物后面，这是由于（）A.汽车一定在上坡B.汽车一定在下坡C.矮建筑物的盲区越来越大D.矮建筑物越来越大Ⅱ.【尝试】例1、如图（1）是两根垂直于地面的旗杆，粗线段表示旗杆甲在太阳光照射下的影子，请你再画出：（1）太阳光线；（2）旗杆乙的影子；\n如图（2）是树和旗杆及它们在灯光下的影子，试确定路灯的位置及小明在路灯下的影子。（2）分析：（1）已知旗杆甲和影子，可确定一条光线，即为太阳能光线，根据同一时刻太阳光线是平行的，便可画出旗杆乙的影子；（2）根据旗杆和影子，树和影子可确定两条光线，它们的交点就是灯的位置。画图（略）提炼：确定一条光线，需要两个点；确定光源的位置，需要两条光线。例1、如图，小灵要到不熟悉地形的某市的新华书店去购书。当他走到大街A处的位置，就断定新华书店不在附近。你说小灵的判断正确吗？为什么？分析：根据盲区的含义画出图形加以判断。解：不正确。新华书店在小灵的盲区内，再往十字路口方向前走若干米即可见。提炼：会利用盲区的含义用“数学的眼光”看世界，体会数学与现实生活的联系。例2、赵亮同学想利用影长测量学校旗杆的高度。如图，他在某一时刻立1米长的标杆，测得其影长为1.2米，同时旗杆的投影一部分在地面上，另一部分在某一建筑物的墙上，分别测得其长度为9.6米和2米，求旗杆的高度。分析：本题难点在于影子落在了两个面上，解决此问题关键是理解当投影面与物体平行时，影长等于其高度。然后再利用在同一时刻影长与物高成比例，或三角形相似来解。解：延长光线AB，与地面交于C，墙上的投影可以看成是竖起的标杆。由已知，得BD：CD=1：1.2，求得CD=2.4，CE=9.6+2.4=12。又由AE：CE=1：1.2，解得AE=10米。提炼：利用在同一时刻影子长度与物体的高度成比例解题，关键是如何理解投影在墙上的影子，不能简单的用地面影子加上墙上影子作为旗杆的投影。例4、已知：CD为一幢3米高的温室，其南面窗户的底框G距地面1米，CD在地面上留下的最大影长CF为2米，现欲在距C点5米的正南方A点处建一幢9米高的楼房AB（设A、C、F在同一水平线上）（1）按比例较精确地作出高楼AB及它的最大影长AE；（2）问：若大楼AB建成后是否影响CD的采光，试说明理由。分析：由CD=3米，按比例易作出9米高的楼房AB；根据物体都取最大影长时太阳光线平行，作出楼房AB的最大影长，并利用太阳光下同一时刻物高与影长成比例，及当物体与投影平面平行时物高与影长相等，求出AB-CG的影长并与AC比较大小即可。解（1）画图略；（2）大楼AB建成后影响CD的采光。理由略。提炼：会利用太阳光下同一时刻物高与影长成比例，及当物体与投影平面平行时物高与影长相等来解决问题。Ⅲ、【小结】：1、本单元知识结构（见填空）2、解题注意点：在太阳光下同一时刻物高与影长成比例，但灯光下不一定成比例。Ⅳ、【实践】教师自行设计作业；复习指导用书第123—124页练习二第6、9、12、13、14题。\n第22课时图形的变换南渡初级中学张旗复习教学目标：1、了解轴对称、平移、旋转这三种图形变化的主要特征和基本性质。2、会判断常见图形的对称性，探索图形之间的变换关系。3、会利用轴对称、平移、旋转的组合进行图案设计。复习教学过程设计一、【唤醒】1、填空：（1）变换类型要求性质研究变换图形的关键翻折沿一条直线翻折______翻折后所得图形与原图形关于这条直线成对称。对应点所连的线段被对称轴________。找对应点找对应边找对应角找对应图形平移需要知道原来的位置及平移的和平移不改变图形的和____对应点的连线____且____。旋转需要知道原来的位置和旋转中心外，还要知道旋转的方向及旋转角度。对应点到旋转中心距离对应点的旋转中心的连线所成的角彼此。（2）如图所示，∠AOB=∠COD=60°,OA=OB,OC=OD,把△AOC绕着点O旋转60°，点A将落在点_____上，点C将落在点_____上，因此，△AOC与△BOD可以通过______变换完全重合。BC（1）（2）（3）AOD第（2）题第（3）题（3）如图，由小正方形组成的L形图中，请你用三种方法分别在上图中添画一个小正方形使它成为轴对称图形。2、判断：（1）旋转变换前后的图形中，对应线段平行且相等，对应角相等。（）（2）关于某直线对称的两个图形，对应角相等，对应点连线平行且相等。（）（3）平移后的图形与原来的图形的对应线段平行且相等。（）3、选择题：（1）如果△ABC和△A1B1C1成中心对称，△A1B1C1和△A2B2C2成轴对称，则△ABC和△A2B2C2有（）A.全等关系B.无全等关系C.可能有全等关系D.以上都不对\n（2）矩形ABCD和A1B1C1D1于点A成中心对称，则四边形BDB1D1是（）AECDBA.矩形B.菱形C.正方形D.梯形（3）如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（）A.2cmB.3cmC.4cmD.5cm\n二、【尝试】ACBO例1、在下面的网格中按要求画出图形，要求：先画出△ABC向下平移5格后的△A1B1C1，再画出ADCBMNO△ABC以点O为旋转中心，沿顺时针方向旋转90°后的△A2B2C2。例1图例2图例2、已知：如图：ABCD（1）画出A1B1C1D1，使A1B1C1D1与ABCD关于直线MN对称；（2）画出A2B2C2D2，使与ABCD关于点O中心对称；（3）A1B1C1D1与A2B2C2D2是对称图形吗？若是，请在图上画出对称轴或对称中心。A提炼：由例1和例2可知，画变换图形应抓住对应点，先画点，再连线。D例3、如图：线段AB绕点O旋转了一个角度后成为线段CD，由于不小心点O被擦掉，你能找到点O的位置吗？CB分析：由于对应点到旋转中心的距离相等，即AO=CO，BO=DO，因此点O既在线段AC的垂直平分线上，又在线段BD的垂直平分线上，帮点O在两垂直平分线的交点上。解答见《复习指导》P116。提炼：对应点连线的中垂线过旋转中心。A例4，（1）操作与证明：如图，O是边长为a的正方形ABCD的中心，将一块半径足够长，圆心角为直角的扇形纸板的圆心放在O点处，并将纸板绕O点旋转。求证：正方形ABCD的边被纸板覆盖部分的总长度为定值a。ANEBDAOOOOCDBCBC（2）尝试与思考：如图，将一块半径足够长的扇形纸板的圆心放在边长为a的正三角形或边长为a的正五边形的中心O点处，并将纸板绕O点旋转。当扇形纸板的圆心角为时，正三角形的边被纸板覆盖部分的总长度为定值a；当扇形纸板的圆心角为时，正五边形的边被纸板覆盖部分的总长度也为定值a。(正多边形的中心即正多边形各边垂直平分线的交点.)\n分析：本题为实验型探究题，解题的关键在于理解题意，按题意动手操作，在动手操作中获得知识，接着把正方形推广到正三角形和正五边形。进而引申到任意正多边形中去，体现了从特殊到一般研究数学问题的方法，有效地考查了学生动手、观察、猜想、归纳、探究的能力。解：（1）略（2）120°,72°提炼：旋转图形时应抓住旋转角，同时引导学生观察猜想。三、【小结】1、知识点见前表2、在翻折、平移、旋转图形的思考中，应抓住对应的点，对应的角和对应的线段研究问题。四、【实践】（1）教师自行设计作业（2）《复习指导用书》第116-120页第1、2、4、5、7、9、10、11、17。第23课时相似形（1）南渡初级中学芮和保复习教学目标：1、知道线段的比、比例线段、黄金分割、相似、位似等概念，了解比例的性质。2、会利用比例的性质进行比例变形，会用相似多边形的性质解决实际问题，能够利用位似将一个图形放大或缩小。3、体会利用从特殊到一般解决问题的方法和分类的数学思想复习教学过程设计：一、【唤醒】1、______________________________2、______________________________3、______________________________1、填空：（1）比例线段（2）比例性质（3）黄金分割：若点C是线段AB的黄金分割点（AC>BC），则AC：AB=_____（4）位似图形的性质：位似图形上任意一对对应点到位似中心的距离等于__________2、判断：（1）、由a∶b=7∶9得7a=9b()（2）、有一个角对应相等的菱形相似（）（3）、如果四边形ABCD和四边形A1B1C1D1是位似图形，且位似比为k，那么=（）（4）、位似图形一定是相似图形，相似图形也一定是位似图形（）3、选择：⑴、A、B两地实际距离AB=250m,画在图上的距离A/B/=5cm,则这幅图的比例尺是----------（）A、1∶50B、50∶1C、1∶5000D、1∶500\n⑵、已知a、b、c、d是成比例线段，且a=4,b=3,c=8,则d等于------------------------()A、B、C、5D、6⑶、已知，下列变形错误的是--------------------------------------------------------------------（）A、(b+d≠0)B、C、D、⑷、已知，则----------------------------------------------------------（）A、B、C、D、2⑸、两个相似多边形的相似比为2∶3，周长之和为65cm，则较大的多边形周长为--------（）A、39cmB、45cmC、cm　D、cm⑹、若点C、D是线段AB的黄金分割点,且AB=1，则CD=-----------------------------------------（）A、B、C、D、　二、【尝试】：例1、已知三条线段长度分别为4、8、5，试写出另一条线段，使这四条线段为成比例线段。分析：这是一道开放题，目的在于考查学生对比例线段概念的理解，题中没有明确告诉具体的比例式，所以本题包含着多种情况。解略，答案：、、10提炼：认真审题，正确应用分类思想，防止漏解。例2、一木框的内外是两个矩形ABCD和EFGH，按图中尺寸，在什么条件下两个矩形相似？分析：这是一道结合比例性质和多边形相似判定的题目，解答本题时，要根据多边形的定义，看题中还缺少判定四边形相似的什么条件，从要找的条件入手列出比例式，再根据比例的性质进行变形。nmbbaaEHGFCDBA解：由题意得：要使两个矩形相似，还须由比例的基本性质得：即当时，两个矩形相似。提炼：当a=b时两个矩形相似，但这只是其中的一种特殊情况。本题属于条件探索题，解题时不要把条件和结论用错了。\n例3、定义：若某个图形可分割为若干个都与他相似的图形，则称这个图形是自相似图形.探究：（1）如图甲，已知△ABC中∠C=900，你能把△ABC分割成4个与它自己相似的小直角三角形吗？若能，请在图甲中画出分割线，并说明理由.BA图甲（2）一般地，“任意三角形都是自相似图形”，只要顺次连结三角形各边中点，则可将原三角形分割为四个都与它自己相似的小三角形.我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割，称为1阶分割（如图1）；把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割，称为2阶分割（如图2）…依次规则操作下去.n阶分割后得到的每一个小三角形都是全等三角形（n为正整数），设此时小三角形的面积为SN，若△DEF的面积为10000，利用计算器探索当n为何值时，21），则纵向上拉长到n倍（压缩到）；纵坐标乘以-1，则图形与原图形关于x轴成轴对称。进而可再类比得出纵坐标不变条件下图形变化规律。例2.△ABC在方格纸中的位置如图所示：（1）请在方格纸上建立平面直角坐标系，使得A，B两点的坐标分别为A（2，-1），B（1-4），并求出C点的坐标；（2）作出△ABC关于横轴对称的△A1B1C1，再作出△ABC以坐标原点为旋转中心，旋转1800后的△A2B2C2，并写出C1、C2两点的坐标；（3）观察△A1B1C1和△A2B2C2，其中的一个三角形能否由另一个三角形经过某种变换而得到？若能，请指出是什么变换。分析：通过作图，利用轴对称、中心对称知识解决。解略〔答案：(1)C(3,-3)；(2)图略C1(3,3),C2(-3,3);(3)能，轴对称〕提炼点：从图形的变换到坐标的变化，在观察，分析时要数形结合。例3．如图，在直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1\n变换成△OA2B2，第三次将△OA2B2变换成△OA3B3，已知A(1，3)，A1(2，3)，A2(4，3)，A3(8，3)；B(2，O)，B1(4，0)，B2(8，0)，B3(16，0)．y(1)观察每次变换前后的三角形有何变化，找出规律，按此变换AA1A2A3规律再将△OA3B3变换成△OA4B4，则A4的坐标是B4的坐标是(2)若按(1)中找到的规律将△OAB进行了n次变换，得到△OAnBn则A。的坐标是,Bn的坐标是。OBB1B2B3分析：要正确地解答本题，就应认真观察A、A1、、、、A2、A3和B、B1、B2、B3的横、纵坐标的特点．通过观察不难发现，A、A1、、、、A2、A3的纵坐标不变，横坐标按2的指数幂递增；B、B1、B2、B3纵坐标为O，横坐标也按2的指数幂递增．由此可得第(1)小题的结论为A4(16，3)，B4(32，0)；也可推出第(2)小题的结论为A。(2n,3),B(2n+1,0).提炼点：探索图形坐标的变化与图形变化的关系，往往要抓住坐标的变与不变，来确定解题的突破口。例4.如图，已知△ABC是边长为4的等边三角形，AB在x轴上，AC与y轴交于点D，点A的坐标为（-1，0），B点坐标为（3，0）求C、D两点的坐标。分析：先确定点C的位置，再经过计算求O点的坐标，求D点的坐标可通过相似或三角函数计算。解略[答案：C点：（1，2）或（1，-2），D点：（0，）或（0，-）。]提炼点：运用数形结合的思想和分类讨论以及转化的思想，将求点的坐标结合图形问题转化为求边长的问题。三、[小结]1.本单元知识结构（见上表）2.本节课用的数学思想方法：类比思想、数形结合思想、分类思想等。四、[实践]复习指导用书第128页第11、12、13题第28课时统计燕山中学王爱军复习教学目标1、知道加权平均数、频数、频率的概念；指出总体、个体、样本；了解三种统计图的联系和区别。2、会求平均数、众数、中位数；会用计算器求方差、标准差；会列频数分布表、画频数分布直方图、折线图。3、能用统计知识解决简单的实际问题。体会用样本估计总体的思想；会对日常生活中的某些数据发表自己的看法，对统计结果作出合理的判断和预测。复习教学过程设计分布状况频数分布直方图频数分布折线图频数数字特征集中趋势波动大小极差众数统计调查的方式总体抽查整理数据的方式折线统计图数字特征分布状况一、【唤醒】1、填空题\n2、判断题（1）n个数的中位数一定是这n个数中的某一个（╳）（2）方差是表示一组数据离散程度的量，方差越大，数据越整齐（╳）（3）要了解全市中学生身高在某一范围内学生所占的比例，需知道相应的频率分布（√）（4）在频数分布直方图中，小长方形的高是该组的频率（╳）（5）如果将所给定的数据组中的每个数都减去一个非零常数，那么该数组的平均数改变，方差改变（╳）3、选择题（1）已知一组数据5，15，25，35，35，45，45，45，75，75那么40是这一组的（B）A、平均数但不是中位数B、平均数也是中位数C、众数D、中位数但不是平均数（2）为了解我校八年级800名学生期中数学考试情况，从中抽取了200名学生的数学成绩进行统计.下列判断：①这种调查方式是抽样调查；②800名学生是总体；③每名学生的数学成绩是个体；④200名学生是总体的一个样本；其中正确的判断有（B）A.、1个B、2个C、3个D、.4个（3）有十五位同学参加智力竞赛，且他们的分数互不相同，取八位同学进入决赛，某人知道了自己的分数后，还需知道这十五位同学的分数的什么量，就能判断他能不能进入决赛（D）A、平均数B、众数C、最高分数D、中位数（4）为了估计湖里有多少条鱼，先捕了100条鱼，做好标记然后放回到湖里，过一段时间，待带有标记的鱼完全混合于鱼群后，再捕上200条鱼，发现其中带有标记的鱼为2条，湖里大约有鱼（C）A、800条B、6000条C、10000条D、1000条（5）已知样本数据为9.9，10.3，10，10.1，9.7，则方差为（B）A、0B、0.04C、0.2D、0.4二、【尝试】例1有100名学生参加两次科技知识测试，条形图显示两次测试的分数分布情况．请你根据条形图提供的信息，回答下列问题（把答案填在题中横线上）；（1）两次测试最低分在第一次测试中；第二次测试第一次测试0~1920~3940~5960~7980~992010学生数分数40300（2）第二次测试较容易；这次测试分数在60～79之间的频率是0.3（3）第一次测试中，中位数在20~39分数段，\n第二次测试中，中位数在40~59分数段．提炼：频数分布直方图的纵坐标表示的量是频数，小长方形越高，频数越大。横坐标表示的量一般是从小到大排列，与求中位数的要求相一致。例2某校组织初三同学外出郊游，下图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图。（1）求该班有多少名学生？（2）在扇形统计图中，求骑车人数所占的圆心角度数。（3）补上步行分布直方图的空缺部分；（4）若全年级有500人，估计该年级步行人数。乘车50%步行20%骑车30%2012乘车步行骑车学生数分析：本例从条形统计图我们可以获取乘车、骑车的人数，从扇形统计图获取乘车、步行、骑车人数所占班级学生人数的百分比。求全年级步行学生可以用样本估计总体。解（略）答案（1）40（2）108°（3）略（4）100提炼：条形统计图、扇形统计图之间的相互转化，关键是抓住在不同图形中乘车与骑车人数不变。补全频数分布直方图要注意小长方形的高与频数成正比。例3快乐公司决定按左图给出的比例，从甲、乙、丙三个工厂共购买200件同种产品A，已知这三个工厂生产的产品A的优品率如右表所示．⑴求快乐公司从丙厂应购买多少件产品Ａ；⑵求快乐公司所购买的200件产品A的优品率；⑶你认为快乐公司能否通过调整从三个工厂所购买的产品A的比例，使所购买的200件产品A的优品率上升3%．若能，请问应从甲厂购买多少件产品A；若不能，请说明理由．③①②①甲25%③丙②乙40%甲乙丙优品率80%85%90%解⑴丙厂：200×（1-25%-40%）＝70⑵甲厂：200×25%＝50；乙厂200×40%=80；优品率(50×80%+80×85%+70×90%)÷200=0.855=85.5%⑶设从甲厂购买x件，从乙厂购买ｙ件，丙厂购买（200―x―y）件．则80%x+85%y+90%(200―x―y)=200×88.5%，即2x+y=60；又80%x和85%y均为整数。所以当y=0时，x=30；当y=20时，x=20；当y=40时，x=10；当y=60时，x=0,提炼：进行加工的能力是学生必备能力。本题把统计知识和不定方程融为一体，解题的关键是注意隐藏条件0.8x、0.85y是整数。即x是5的倍数，y是20的倍数三、【小结】1、带领学生回顾尝试中的填空题。2、数形转化、从图表、数据、文字获取信息是统计的主线，用统计知识解决生活中的实际问题是我们学习的目的。四、【实践】（1）教师自行设计作业（2）复习指导：144页练习一6、148页12、\n第29课时概率燕山中学王爱军复习教学目标：1、了解确定事件、可能事件的概念及内涵；知道实验次数充分大时，可以用实验频率估计理论概率。2、会估计不确定事件发生可能性的大小，会求单一事件概率；会用列举法（列表法、画树状图）计算简单事件的概率；会用概率判定游戏是否公平。3、会用概率解决生活中的一些实际问题。复习教学过程设计一、唤醒：事件确定事件必然事件概率求二次操作事件的概率树状图求一次操作事件的概率1、填空题：2、判断题：（1）买一张奖券，不中奖是不太可能（×）（2）东北的冬天会下雪是确定事件（√）（3）你和同学周日单独逛商场会相遇很可能（×）（4）小王同学的身高能长到3m是不可能事件（√）（5）从一副扑克牌中任意抽出一张扑克牌，抽到红色牌是可能事件（√）3、选择题：(1)某商店举办有奖销售活动，购物满100元者发对奖券一张．在10000张奖券中，设特等奖1个，一等奖10个，二等奖100个．若某人购物刚好满100元，那么他中一等奖的概率是（B）A、B、C、D、(2)一个转盘被划分成六个相同大小的扇形，并分别标上1，2，3，4，5，6这六个数字，指针停在每个扇形的可能性相等．四位同学各自发表了下述见解：甲：如果指针前三次都停在了3号扇形，下次就一定不会停在3号扇形乙：只要转盘连续转六次，一定会有一次指针停在6号扇形丙：指针停在奇数号扇形的概率与停在偶数号扇形的概率相等丁：运气好的时候，只要在转动前默默想好让指针停在6号扇形，指针停在6号扇形的可能性就会加大.其中，你认为正确的见解有（A）A、1个B、2个C、3个D、4个\n(3)在“抛一枚均匀硬币”的实验中，如果现在没有硬币，则下面各个试验中哪个不能代替（C）A、两张扑克，“黑桃”代替“正面”，“红桃”代替“反面”B、两个形状大小完全相同，但一红一白的两个乒乓球C、扔一枚图钉D、人数均等的男生、女生，以抽签的方式随机抽取一人(4)一个袋中里有4个珠子，其中2个红色，2个蓝色，除颜色外其余特征均相同，若从这个袋中任取2个珠子，都是蓝色珠子的概率是（D）A、　　　B、　　　C、　　　D．二、尝试：例1：从分别标有1、2、3、4、5的5张卡片中任选2张，求：（1）2张的号数之和为5的概率（2）它们互质（没有大于1的公因数）的概率（3）它们的乘积超过5的概率（4）它们的乘积超过10的概率分析：本例复习用列表法或树状图求概率，解（略）答案0.2、0.9、0.6、0.3提炼：解题要注意摸取卡片不能有重复，即如果第一张摸出1后，第二张不可能是1例2：已知集合A=，B=，C=，且它们分别表示包含这些线段长度的集合，如果分别从集合A、B、C中任意选取一个长度，请回答下列问题：（1）以选取的三个长度的线段能够构成三角形的概率是多少？（2）以选取的三个长度的线段能够构成等腰三角形的概率是多少？（3）以选取的三个长度的线段能够构成等边三角形的概率是多少？分析：本例无法用列表法求概率，复习用画树状图求概率。解答见《复习指导》P136提炼：例题中有三个变量，无法用列表法求解，只能用树状图将所有情况一一列出，然后通过找出符合要求的情况求出概率例3：集市上有一个人在设摊“摸彩”，只见他手拿一个黑色的袋子，内装大小、形状、质量完全相同的白球20只，且每一个球上都写有号码（1－20号）和1只红球，规定：每次只摸一只球．摸前交1元钱且在1——20内写一个号码，摸到红球奖5元，摸到号码数与你写的号码相同奖10元．（1）求摸彩者获奖的概率．（2）若一个“摸彩”者多次摸奖后，他平均每次将获利或损失多少元？说明你的理由.分析：（1）获奖概率有两部分组成，摸到红球奖和摸到号码数与你写的号码相同。（2）一个试验多次重复后，概率接近频率，可以用概率代替频率进行计算解：（1）P=（2）（元）提炼：例题联系生活，用数学知识解决生活中一些实际问题，有助于我们提高警惕，防止上当受骗。例4：（思考题）如下图是9×\n7的正方形点阵，其水平方向和竖直方向的两格点间的长度都为1个单位，以这些点为顶点的三角形称为网格三角形．请通过画图分析、探究回答下列问题：(1)请在图中画出以AB为边且面积为2的一个网格三角形．(2)任取该网格中的一点M，求以A、B、M为顶点的三角形的面积为2的概率．(3)任取该网格中的一点M，求以A、B、M为顶点的三角形为直角三角形的概率．分析：例题是一道动手操作和几何知识相结合，通过操作探求动点M的特殊位置，（2）注意同底等高的三角形面积相等，符合条件的直线有两条。（3）三角形为直角三角形，但直角顶点不确定，所以要分类画图，以A为直角顶点，B为直角顶点，M为直角顶点，特别是M为直角顶点，M在AB中垂线上。找出符合条件的所有点，再求概率解：（1）略（2）P=（3）P=提炼：例题解答要注意数形结合和分类思想，同时考虑问题要全面，防止遗漏。三、小结：带领学生回顾尝试中的填空题，注意解概率题的基本方法和注意点。四、实践：（1）教师自行设计作业（2）复习指导：134页练习一1～6，136页练习二1、2、5、6、8、12袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈葿螈聿蒄葿袁羁莀蒈羃膇芆蒇蚃羀膂蒆螅膅蒁薅袇羈莇薄罿膄芃薃虿羆艿薃袁节膅薂羄肅蒃薁蚃芀荿薀螆肃芅蕿袈芈膁蚈羀肁蒀蚇蚀袄莆蚇螂肀莂蚆羅袂芈蚅蚄膈膄蚄螇羁蒂蚃衿膆莈蚂羁罿芄螁蚁膄膀螁螃羇葿螀袅膃蒅蝿肈羆莁螈螇芁芇莄袀肄膃莄羂艿蒂莃蚂肂莈蒂螄芈芄蒁袆肀膀蒀罿袃薈羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿袈聿蚇蒂膇肈莇螇肃肇葿薀罿肆薂螆袅肅芁薈螁膅莃螄聿膄蒆薇羅膃蚈螂羁膂莈蚅袇膁蒀袀螃膀薂蚃肂腿节衿羈腿莄蚂袄芈蒇袇螀芇蕿蚀聿芆艿蒃肅芅蒁螈羁芄薃薁袆芃芃螆螂芃莅蕿肁节蒈螅羇莁薀薈袃莀艿螃蝿荿莂薆膈莈薄袁肄莇蚆蚄羀莇莆袀袆羃蒈蚂螂羂薁袈肀肁芀蚁羆肁莃袆袂肀薅虿