初中三角函数知识点总结(中考复习) 9页

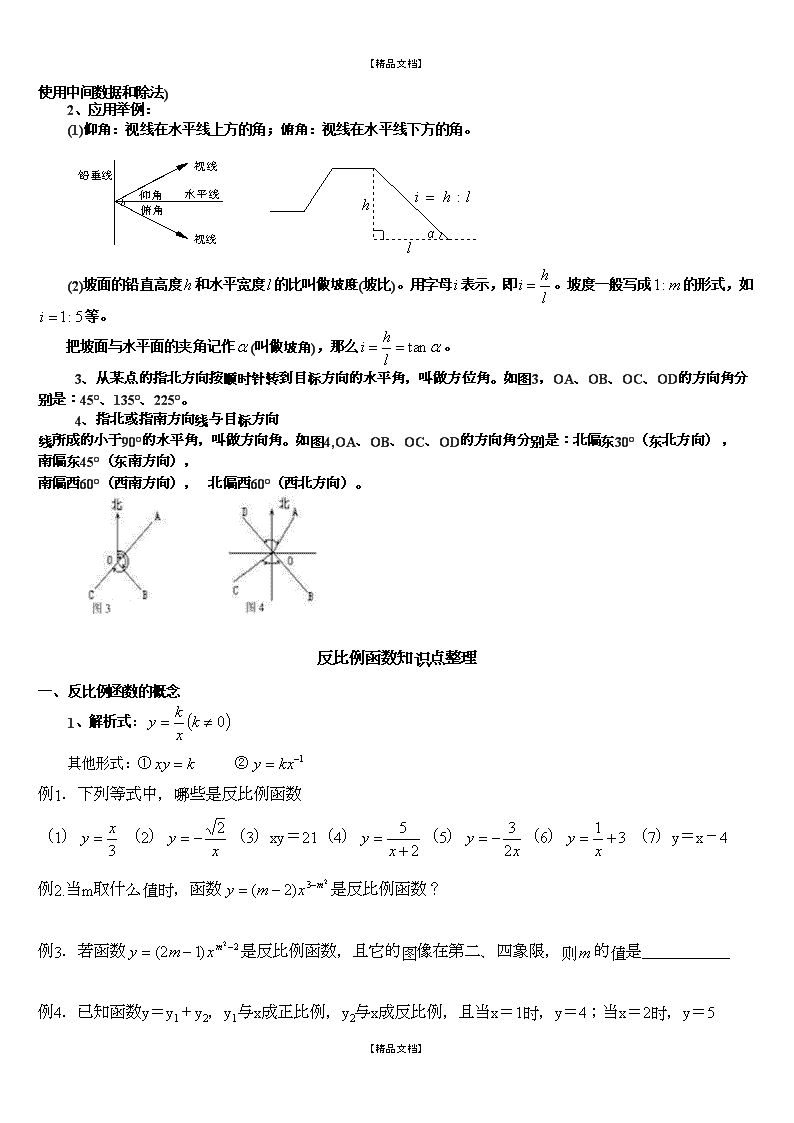
------------------------------------------作者xxxx------------------------------------------日期xxxx初中三角函数知识点总结(中考复习)\n【精品文档】锐角三角函数知识点总结1、勾股定理：直角三角形两直角边、的平方和等于斜边的平方。2、如下图，在Rt△ABC中，∠C为直角，则∠A的锐角三角函数为(∠A可换成∠B)：定义表达式取值范围关系正弦(∠A为锐角)余弦(∠A为锐角)正切(∠A为锐角)(倒数)余切(∠A为锐角)对边邻边斜边ACB3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)三角函数0°30°45°60°90°011001不存在不存在106、正弦、余弦的增减性：当0°≤≤90°时，sin随的增大而增大，cos随的增大而减小。7、正切、余切的增减性：当0°<<90°时，tan随的增大而增大，cot随的增大而减小。1、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。依据：①边的关系：；②角的关系：A+B=90°；③边角关系：三角函数的定义。(【精品文档】\n【精品文档】注意：尽量避免使用中间数据和除法)2、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。(2)坡面的铅直高度和水平宽度的比叫做坡度(坡比)。用字母表示，即。坡度一般写成的形式，如等。把坡面与水平面的夹角记作(叫做坡角)，那么。3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。如图3，OA、OB、OC、OD的方向角分别是：45°、135°、225°。4、指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角。如图4,OA、OB、OC、OD的方向角分别是：北偏东30°（东北方向），南偏东45°（东南方向），南偏西60°（西南方向），北偏西60°（西北方向）。反比例函数知识点整理一、反比例函数的概念1、解析式：其他形式：①②例1．下列等式中，哪些是反比例函数（1）（2）（3）xy＝21（4）（5）（6）（7）y＝x－4例2.当m取什么值时，函数是反比例函数？例3．若函数是反比例函数，且它的图像在第二、四象限，则的值是___________例4．已知函数y＝y1＋y2，y1与x成正比例，y2与x成反比例，且当x＝1时，y＝4；当x＝2时，y＝5【精品文档】\n【精品文档】（1）求y与x的函数关系式（2）当x＝－2时，求函数y的值2.反比例函数图像上的点的坐标满足：例1．已知反比例函数的图象经过点（m，2）和（-2，3）则m的值为　　　　　例2．下列函数中，图像过点M（-2，1）的反比例函数解析式是()例3.如果点（3，－4）在反比例函数的图象上，那么下列各点中，在此图象上的是（）A.（3,4）　　B.　（－2，－6）　　C.（－2，6）　　D.（－3，－4）例4.如果反比例函数的图象经过点（3，－1），那么函数的图象应在（）A．第一、三象限　B．第二、四象限C．第一、二象限　D．第三、四象限二、反比例函数的图像与性质1、基础知识时，图像在一、三象限，在每一个象限内，y随着x的增大而减小；时，图像在二、四象限，在每一个象限内，y随着x的增大而增大；，当时，y随x的增大而增大，求函数关系式例2．已知反比例函数的图象在每个象限内函数值y随自变量x的增大而减小，且k的值还满足≥2k－1，若k为整数，求反比例函数的解析式2、面积问题（1）三角形面积：pyAxO例1.如图，过反比例函数（x＞0）的图象上任意两点A、B分别作x轴的垂线，垂足分别为C、D，连接OA、OB，设△AOC和△BOD的面积分别是S1、S2，比较它们的大小，可得（）（A）S1＞S2（B）S1＝S2（C）S1＜S2（D）大小关系不能确定【精品文档】\n【精品文档】例2.如图，点P是反比例函数的图象上任一点，PA垂直在轴，垂足为A，设的面积为S，则S的值为　　　　　例3．直线OA与反比例函数的图象在第一象限交于A点，AB⊥x轴于点B，若△OAB的面积为2，则k＝.例4．如图，若点在反比例函数的图象上，轴于点，的面积为3，则．例5．如图，在轴的正半轴上依次截取，过点分别作轴的垂线与反比例函数的的图象相交于点，得直角三角形并设其面积分别为则的值为.例6．如图，A、B是函数的图象上关于原点对称的任意两点，BC∥轴，AC∥轴，△ABC的面积记为，则（）A．B．C．D．（2）矩形面积：例1．如图，P是反比例函数图象上的一点，由P分别向x轴和y轴引垂线，阴影部分面积为3，则k=。例2．如图，已知点C为反比例函数上的一点，过点C向坐标轴引垂线，垂足分别为A、B，那么四边形AOBC的面积为．例3图例3．如图，点、是双曲线上的点，分别经过、两点向轴、轴作垂线段，若则．例4、如图，矩形AOCB的两边OC，OA分别位于x轴，y轴上，点B的坐标为B（，5），D是AB边上的一点，将△ADO沿直线OD翻折，使A【精品文档】\n【精品文档】点恰好落在对角线OB上的点E处，若点E在一反比例函数的图像上，那么该函数的解析式是______．y=和y=在第一象限内的图像如图3所示，点P在y=的图像上，PC⊥x轴于点C，交y=的图像于点A，PD⊥y轴于点D，交y=的图像于点B，当点P在y=的图像上运动时，以下结论：①△ODB与△OCA的面积相等；②四边形PAOB的面积不会发生变化；③PA与PB始终相等④当点A是PC的中点时，点B一定是PD的中点．其中一定正确的是_______（把你认为正确结论的序号都填上，少填或错填不给分）．（1）比较点的坐标大小例1．已知点（－1，y1）、（2，y2）、（π，y3）在双曲线上，则下列关系式正确的是（）（A）y1＞y2＞y3（B）y1＞y3＞y2（C）y2＞y1＞y3（D）y3＞y1＞y2例2．已知三点，，都在反比例函数的图象上，若，，则下列式子正确的是（）A．B．C．D．例3．反比例函数，当x＝－2时，y＝；当x＜－2时；y的取值范围是；当x＞－2时；y的取值范围是例4.点A(2，1)在反比例函数的图像上，当1﹤x﹤4时，y的取值范围是.例5．若A(，)、B(，)在函数的图象上，则当、满足________时，＞.【精品文档】\n【精品文档】例6．在反比例函数的图象上有两点A，B，当时，有，则的取值范围是（）A、B、C、D、例7、已知反比例函数的图像上有两点A(，)，B(，)，且，则的值是（）A、正数B、负数C、非正数D、不能确定（2）比较函数值大小例1．如图是一次函数y1=kx+b和反比例函数y2=的图象，观察图象写出y1＞y2时，的取值范围例2．如图,一次函数ｙ=ｘ－1与反比例函数ｙ=的图像交于点A(2,1),B(－1,－2),则使ｙ＞ｙ的ｘ的取值范围是（）A.ｘ＞2B.ｘ＞2或－1＜ｘ＜0C.－1＜ｘ＜2D.ｘ＞2或ｘ＜－1三、反比例函数与一次函数的综合题（1）在同一坐标系中的图像问题例1．一次函数与反比例函数在同一直角坐标系内的大致图象是（）例2．函数y＝－ax＋a与（a≠0）在同一坐标系中的图象可能是（）【精品文档】\n【精品文档】xy（2）其他类型例1．如图，已知一次函数的图象与反比例函数的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是，求：（1）一次函数的解析式；（2）△AOB的面积．例2．如图，在直角坐标系中，直线y=6-x与函数y=(x>0)的图象相交于点A、B，设点A的坐标为(x1，，y1)，那么长为x1,宽为y1的矩形面积和周长分别为()A．4，12B．8，12C．4，6D．8,6CBxODAy例3．如图：已知一次函数的图象与轴、轴分别交于、两点，且与反比例函数的图象在第一象限交于点，⊥轴，垂足为，若（1）求点、、的坐标；（2）求一次函数与反比例函数的解析式；；yxAOB例4：如图，反比例函数的图象与一次函数的图象交于，两点．[来源:（1）求反比例函数与一次函数的解析式；（2）根据图象回答：当取何值时，反比例函数的值大于一次函数的值【精品文档】\n【精品文档】例5.如图，A、B是反比例函数y＝的图象上的两点。AC、BD都垂直于x轴，垂足分别为C、D。AB的延长线交x轴于点E。若C、D的坐标分别为（1，0）、（4，0），则ΔBDE的面积与ΔACE的面积的比值是（）A．B．Ｃ．D．三、反比例函数的应用例1．已知甲、乙两地相s（千米），汽车从甲地匀速行驶到达乙地，如果汽车每小时耗油量为a（升），那么从甲地到乙地汽车的总耗油量y（升）与汽车的行驶速度v（千米/时）的函数图象大致是（）例2．一张正方形的纸片，剪去两个一样的小矩形得到一个“”图案，如图所示，设小矩形的长和宽分别为、，剪去部分的面积为20，若，则与的函数图象是（　　　）【精品文档】