初中几何证明中考压轴全国初中数学联赛必做100题第二部 7页

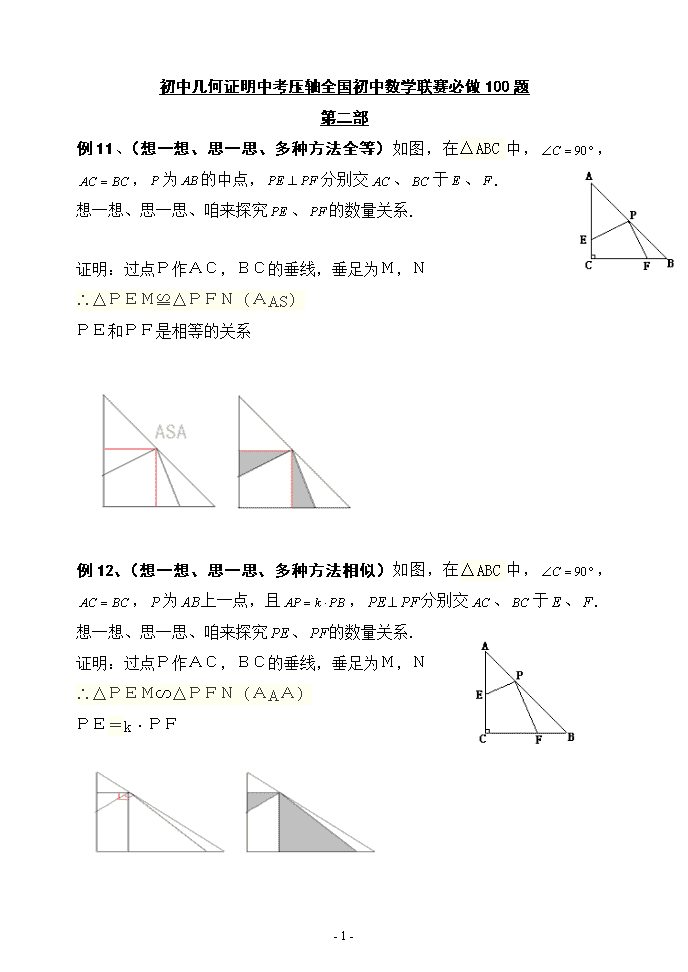
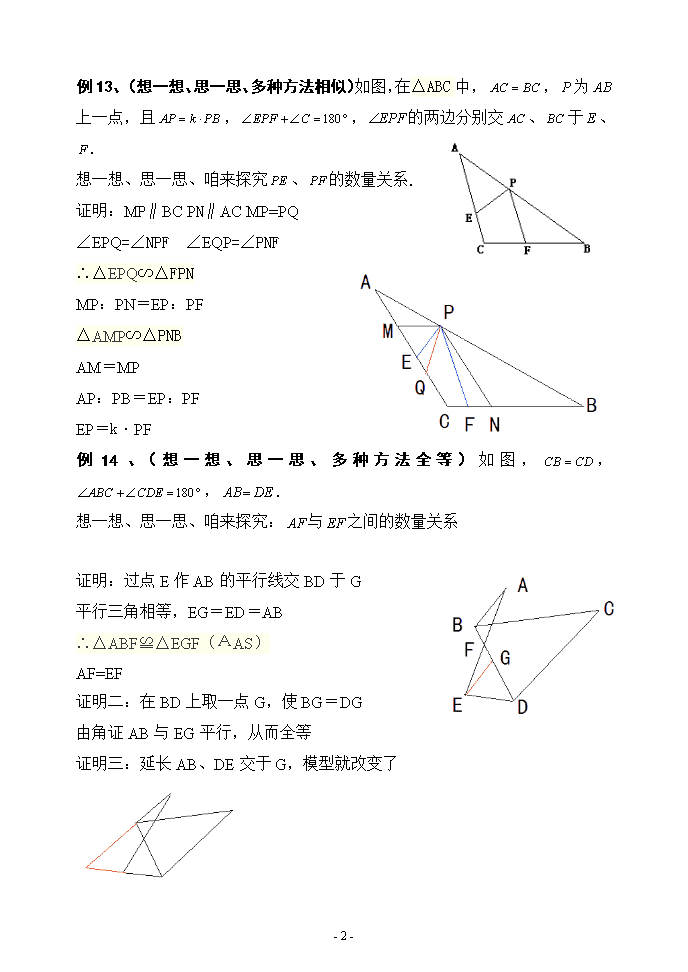
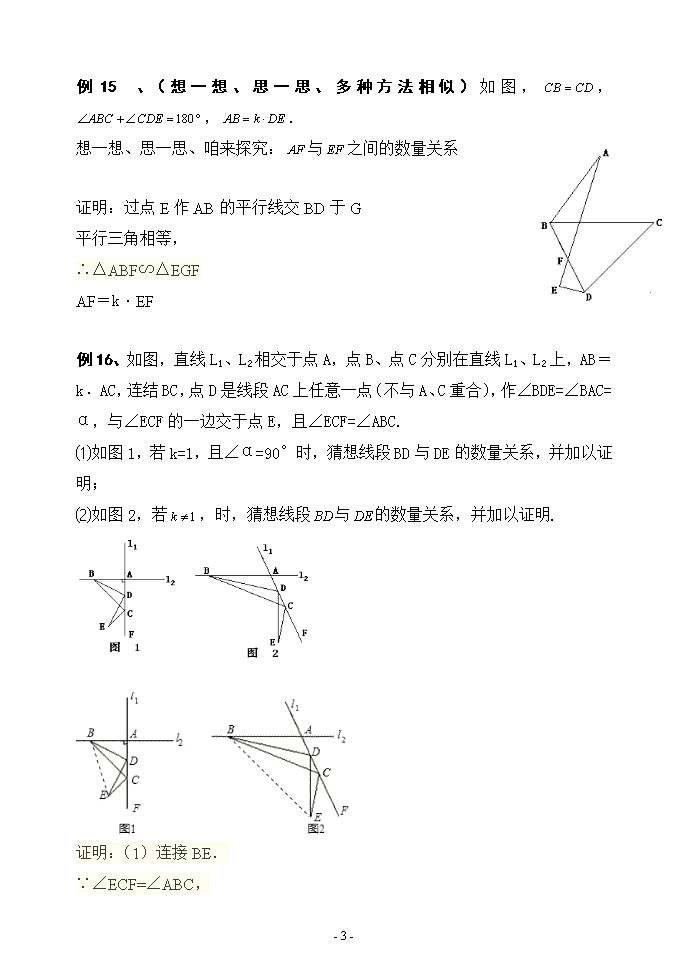
初中几何证明中考压轴全国初中数学联赛必做100题第二部例11、（想一想、思一思、多种方法全等）如图，在△ABC中，，，为的中点，分别交、于、.想一想、思一思、咱来探究、的数量关系.证明：过点Ｐ作ＡＣ，ＢＣ的垂线，垂足为Ｍ，Ｎ∴△ＰＥＭ≌△ＰＦＮ（ＡAS）ＰＥ和ＰＦ是相等的关系例12、（想一想、思一思、多种方法相似）如图，在△ABC中，，，为上一点，且，分别交、于、.想一想、思一思、咱来探究、的数量关系.证明：过点Ｐ作ＡＣ，ＢＣ的垂线，垂足为Ｍ，Ｎ∴△ＰＥＭ∽△ＰＦＮ（ＡAＡ）ＰＥ＝k·ＰＦ-7-\n例13、（想一想、思一思、多种方法相似）如图，在△ABC中，，为上一点，且，，的两边分别交、于、.想一想、思一思、咱来探究、的数量关系.证明：MP∥BCPN∥ACMP=PQ∠EPQ=∠NPF∠EQP=∠PNF∴△EPQ∽△FPNMP：PN＝EP：PF△AMP∽△PNBAM＝MPAP：PB＝EP：PFEP＝k·PF例14、（想一想、思一思、多种方法全等）如图，，，.想一想、思一思、咱来探究：与之间的数量关系证明：过点E作AB的平行线交BD于G平行三角相等，EG＝ED＝AB∴△ABF≌△EGF（ＡAS）AF=EF证明二：在BD上取一点G，使BG＝DG由角证AB与EG平行，从而全等证明三：延长AB、DE交于G，模型就改变了-7-\n例15、（想一想、思一思、多种方法相似）如图，，，.想一想、思一思、咱来探究：与之间的数量关系证明：过点E作AB的平行线交BD于G平行三角相等，∴△ABF∽△EGFAF＝k·EF例16、如图，直线L1、L2相交于点A，点B、点C分别在直线L1、L2上，AB＝k﹒AC，连结BC，点D是线段AC上任意一点（不与A、C重合），作∠BDE=∠BAC=α，与∠ECF的一边交于点E，且∠ECF=∠ABC.⑴如图1，若k=1，且∠α=90°时，猜想线段BD与DE的数量关系，并加以证明；⑵如图2，若，时，猜想线段与的数量关系，并加以证明.证明：（1）连接BE．∵∠ECF=∠ABC，-7-\n∠ECF+∠BCE+∠BCA=∠ABC+∠BAC+∠BCA=180°，∴∠BCE=∠BAC；∵∠BDE=∠BAC=α=90°，∴B、E、D、C四点共圆，∴∠BED=∠BCA，∴△BED∽△BCA，∴BD：DE=AB：AC=k=1，∴BD=DE．（2）连接BE．∵∠ECF=∠ABC，∠ECF+∠BCE+∠BCA=∠ABC+∠BAC+∠BCA=180°，∴∠BCE=∠BAC；∵∠BDE=∠BAC=α，∴B、E、D、C四点共圆，∴∠BED=∠BCA，∴△BED∽△BCA，∴BD：DE=AB：AC=k，∴BD=k•DE．问题解析（1）连接BE．若k=1，且∠α=90°时，要求线段BD与DE的数量关系，可以通过证明△BED∽△BCA得出；（2）连接BE．若k≠1，且∠α≠90°时，要求线段BD与DE的数量关系，可以通过证明△BED∽△BCA得出．名师点评本题考点：确定圆的条件；圆周角定理．考点点评：本题考查了圆周角定理，相似三角形的判定和性质，综合性较强，有一定的难度．解题的关键是确定B、E、D、C四点共圆．-7-\n二．倍长中线法：例17、（想一想、思一思、多种方法全等）如图，点是中点，，求证：例18、（想一想、思一思、多种方法相似）如图，AD是△ABC的中线，AB＝k﹒AC，点E是AC延长线上一点，且∠AEF=∠BAD，EF交BA延长线于点F.想一想、思一思、咱来探究AE、AF的数量关系.-7-\nAE=kAF证明：延长AD到G,使DG=AD,连接BG、CG,则ABGC是平行四边形,AB∥=CG∴∠BAG=∠AGC就是∠BAD=∠AGC而∠BAD=∠AEF∴∠AGC=∠AEF又∠FAE=∠ACG(平行线内错角相等)∴△AEF∼△CGA∴AE/AF=CG/AC∴AE/AF=AB/AC因为AB=kAC∴AE=kAF例19、（想一想、思一思、多种方法全等）如图，在△ABC中，，，是边的中线.求证：证明：延长AE到F，使EF＝AE∠ADC＝∠B+∠BAD＝∠BDA+∠BDF＝∠ADF　　AB＝BD＝CD＝DF∴△ADF≌△ADC（SAS）AC＝2AE例20、（想一想、思一思、多种方法相似）如图，在△ABC中，，，是边的中线，且.想一想、思一思、咱来探究、的数量关系.证明：延长AE到F，使EF＝AE-7-\n∠ADC＝∠B+∠BAD＝∠BDA+∠BDF＝∠ADF∴△FDA∽△ADCAE＝k·AC-7-