初中中考平面几何动点类问题压轴题精选 12页

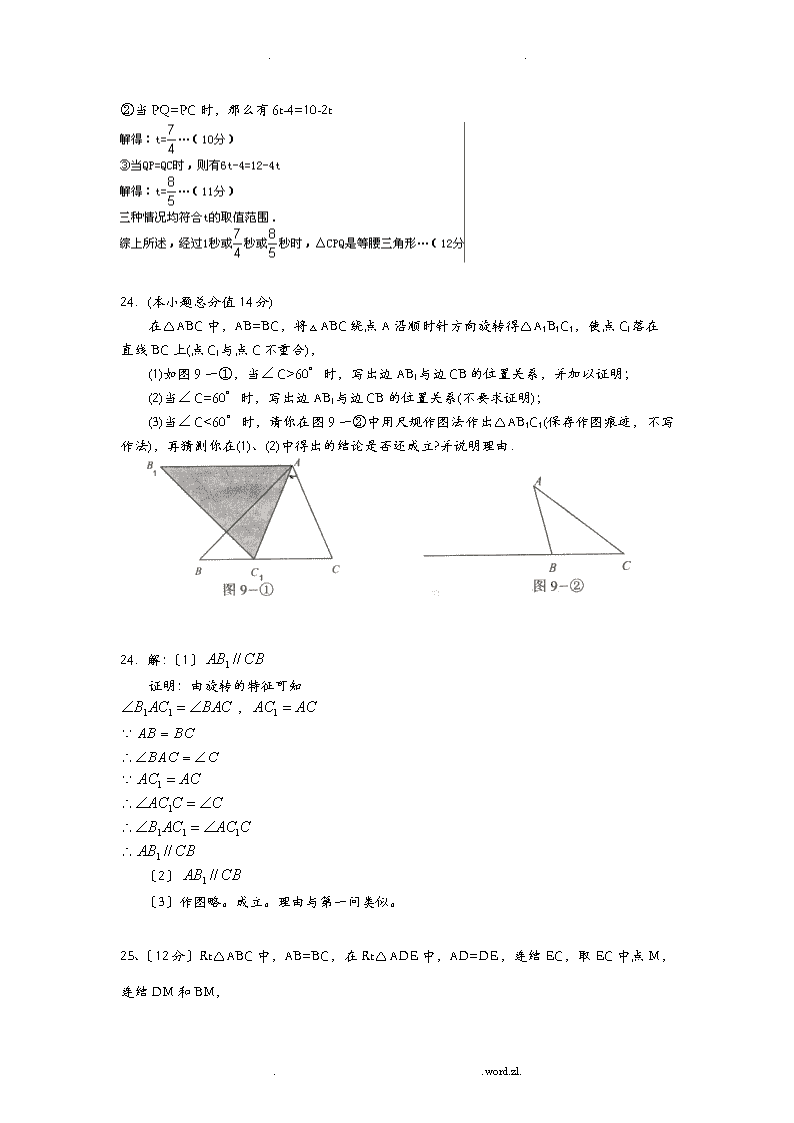
..〔2011•〕如图，在Rt△ABC中，∠B=90°，BC=5，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停顿运动．设点D、E运动的时间是t秒〔t＞0〕．过点D作DF⊥BC于点F，连接DE、EF．〔1〕求证：AE=DF；〔2〕四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．〔3〕当t为何值时，△DEF为直角三角形？请说明理由．解答：〔1〕证明：在△DFC中，∠DFC=90°，∠C=30°，DC=2t，∴DF=t．又∵AE=t，∴AE=DF．〔2分〕〔2〕解：能．理由如下：∵AB⊥BC，DF⊥BC，∴AE∥DF．又AE=DF，∴四边形AEFD为平行四边形．〔3分〕∵AB=BC•tan30°=5=5，∴AC=2AB=10．∴AD=AC﹣DC=10﹣2t．假设使▱AEFD为菱形，那么需AE=AD，即t=10﹣2t，t=．即当t=时，四边形AEFD为菱形．〔5分〕〔3〕解：①∠EDF=90°时，四边形EBFD为矩形．在Rt△AED中，∠ADE=∠C=30°，∴AD=2AE．即10﹣2t=2t，t=．〔7分〕②∠DEF=90°时，由〔2〕知EF∥AD，∴∠ADE=∠DEF=90°．∵∠A=90°﹣∠C=60°，∴AD=AE•cos60°．..word.zl.\n..即10﹣2t=t，t=4．〔9分〕③∠EFD=90°时，此种情况不存在．综上所述，当t=或4时，△DEF为直角三角形．〔10分〕如图，△ABC中，AB=AC=12cm，BC=10cm，点D为AB的中点．如果点P在线段BC上以2cm/s的速度由点B向C点运动，同时，点Q在线段AC上由点A向C点以4cm/s的速度运动．〔1〕假设点P、Q两点分别从B、A两点同时出发，经过2秒后，△BPD与△CQP是否全等，请说明理由；〔2〕假设点P、Q两点分别从B、A两点同时出发，△CPQ的周长为18cm，问：经过几秒后，△CPQ是等腰三角形？解：〔1〕，△BPD与△CQP是全等．理由如下：当P，Q两点分别从B，A两点同时出发运动2秒时有BP=2×2=4cm，AQ=4×2=8cm那么CP=BC-BP=10-4=6cmCQ=AC-AQ=12-8=4cm…〔2分〕∵D是AB的中点∴BD=1/2AB=1/2×12=6cm∴BP=CQ，BD=CP…〔3分〕又∵△ABC中，AB=AC∴∠B=∠C…〔4分〕在△BPD和△CQP中BP=CQ∠B=∠CBD=CP∴△BPD≌△CQP〔SAS〕…〔6分〕 〔2〕设当P，Q两点同时出发运动t秒时，有BP=2t，AQ=4t∴t的取值围为0＜t≤3那么CP=10-2t，CQ=12-4t…〔7分〕∵△CPQ的周长为18cm，∴PQ=18-〔10-2t〕-〔12-4t〕=6t-4…〔8分〕要使△CPQ是等腰三角形，那么可分为三种情况讨论：①当CP=CQ时，那么有10-2t=12-4t解得：t=1…〔9分〕..word.zl.\n..②当PQ=PC时，那么有6t-4=10-2t24．(本小题总分值14分)在△ABC中，AB=BC，将ABC绕点A沿顺时针方向旋转得△A1B1C1，使点Cl落在直线BC上(点Cl与点C不重合)，(1)如图9一①，当C>60°时，写出边ABl与边CB的位置关系，并加以证明；(2)当C=60°时，写出边ABl与边CB的位置关系(不要求证明)；(3)当C<60°时，请你在图9一②中用尺规作图法作出△AB1C1(保存作图痕迹，不写作法)，再猜测你在(1)、(2)中得出的结论是否还成立?并说明理由．24．解：〔1〕证明：由旋转的特征可知，∵∴∵∴∴∴〔2〕〔3〕作图略。成立。理由与第一问类似。25、〔12分〕Rt△ABC中，AB=BC，在Rt△ADE中，AD=DE，连结EC，取EC中点M，连结DM和BM，..word.zl.\n..〔1〕假设点D在边AC上，点E在边AB上且与点B不重合，如图①，求证：BM=DM且BM⊥DM；〔2〕如图①中的△ADE绕点A逆时针转小于45°的角，如图②，那么〔1〕中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明。25.本小题主要考察三角形、图形的旋转、平行四边形等根底知识，考察空间观念、演绎推理能力．总分值12分．〔1〕证法1：在Rt△EBC中，M是斜边EC的中点，∴．在Rt△EDC中，M是斜边EC的中点，∴．∴BM=DM，且点B、C、D、E在以点M为圆心、BM为半径的圆上．∴∠BMD=2∠ACB=90°，即BM⊥DM．证法2：证明BM=DM与证法1一样，下面证明BM⊥DM．∵DM=MC，∴∠EMD=2∠ECD．∵BM=MC，∴∠EMB=2∠ECB．..word.zl.\n..∴∠EMD＋∠EMB=2〔∠ECD＋ECB〕．∵∠ECD＋∠ECB=∠ACB=45°，∴∠BMD=2∠ACB=90°，即BM⊥DM．〔2〕当△ADE绕点A逆时针旋转小于45°的角时，〔1〕中的结论成立．证明如下：证法1〔利用平行四边形和全等三角形〕：连结BD，延长DM至点F，使得DM=MF，连结BF、FC，延长ED交AC于点H．MDBACEHF∵DM=MF，EM=MC，∴四边形CDEF为平行四边形.∴DE∥CF，ED=CF.∵ED=AD,∴AD=CF.∵DE∥CF，∴∠AHE=∠ACF．∵,，∴∠BAD=∠BCF.又∵AB=BC,∴△ABD≌△CBF.∴BD=BF，∠ABD=∠CBF.∵∠ABD+∠DBC=∠CBF+∠DBC，∴∠DBF=∠ABC=90°.在Rt△中，由,，得BM=DM且BM⊥DM．证法2〔利用旋转变换〕：连结BD，将△ABD绕点B逆时针旋转90°，点A旋转到点C，点D..word.zl.\n..旋转到点，得到△，那么且．连结．∵MDBACE∴．又∵，∴四边形为平行四边形．∴D、M、三点共线，且．在Rt△中，由,，得BM=DM且BM⊥DM．证法3〔利用旋转变换〕：连结BD，将△ABD绕点B逆时针旋转90°，点A旋转到点C，点D旋转到点，得到△，那么且．连结，延长ED交AC于点H．∵∠AHD=90°－∠DAH=90°－(45°－∠BAD)=45°＋∠BAD，，∵，MDBACEH∴．∴．又∵，∴四边形为平行四边形．∴D、M、三点共线，且．..word.zl.\n..在Rt△中，由,，得BM=DM且BM⊥DM．4、〔14分〕如图10，扇形OAB的半径OA=3，圆心角∠AOB=90°，点C是上异于A、B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连结DE，点G、H在线段DE上，且DG=GH=HE〔1〕求证：四边形OGCH是平行四边形〔2〕当点C在上运动时，在CD、CG、DG中，是否存在长度不变的线段？假设存在，请求出该线段的长度〔3〕求证：是定值图1024．〔1〕连结OC交DE于M，由矩形得OM＝CG，EM＝DM　　　　因为DG=HE所以EM－EH＝DM－DG得HM＝DG〔2〕DG不变，在矩形ODCE中，DE＝OC＝3，所以DG＝1〔3〕设CD＝x,那么CE＝，由得CG＝　　所以所以HG＝3－1－所以3CH2＝所以..word.zl.\n..24.〔本小题总分值14分〕如图12，边长为1的正方形ABCD被两条与边平行的线段EF、GH分割为四个小矩形，EF与GH交于点P。〔1〕假设AG=AE，证明：AF=AH；〔2〕假设∠FAH=45°，证明：AG+AE=FH；〔3〕假设RtΔGBF的周长为1，求矩形EPHD的面积。24.〔本小题总分值14分〕解：(1)易证ΔABF≌ΔADH,所以AF=AH(2)如图，将ΔADH绕点A顺时针旋转90度，如图，易证ΔAFH≌ΔAFM,得FH=MB+BF,即：FH=AG+AE(3)设PE=x,PH=y,易得BG=1-x,BF=1-y,FG=x+y-1,由勾股定理，得〔1-x〕2+〔1-y〕2=(x+y-1)2,化简得xy=0.5,所以矩形EPHD的面积为0.5.2．〔2010，25，14分〕如下图，四边形OABC是矩形，点A、C的坐标分别为〔3，0〕，〔0，1〕，点D是线段BC上的动点〔与端点B、C不重合〕，过点D作直线＝－＋交折线OAB于点E．〔1〕记△ODE的面积为S，求S与的函数关系式；〔2〕当点E在线段OA上时，假设矩形OABC关于直线DE的对称图形为四边形OA1B1C1，试探究OA1B1C1与矩形OABC的重叠局部的面积是否发生变化，假设不变，求出该重叠局部的面积；假设改变，请说明理由...word.zl.\n..CDBAEO【答案】〔1〕由题意得B〔3，1〕．假设直线经过点A〔3，0〕时，那么b＝假设直线经过点B〔3，1〕时，那么b＝假设直线经过点C〔0，1〕时，那么b＝1①假设直线与折线OAB的交点在OA上时，即1＜b≤，如图25-a，图1此时E〔2b，0〕∴S＝OE·CO＝×2b×1＝b②假设直线与折线OAB的交点在BA上时，即＜b＜，如图2图2此时E〔3，〕，D〔2b－2，1〕∴S＝S矩－(S△OCD＋S△OAE＋S△DBE)＝3－[(2b－1)×1＋×(5－2b)·()＋×3()]＝..word.zl.\n..∴如图，在梯形ABCD中，AD∥BC，AD=3，DC=5，AB=，∠B=45°，动点M从点B出发，沿线段BC以每秒1个单位长度的速度向终点C运动；动点N同时从C点出发，沿C→D→A，以同样速度向终点A运动，当其中一个动点到达终点时，另一个动点也随之停顿运动．设运动的时间为t秒．〔1〕求线段BC的长度；〔2〕求在运动过程中形成的△M的面积S与运动的时间t之间的函数关系式，并写出自变量t的取值围；并求出当t为何值时，△M的面积S最大，并求出最大面积；〔3〕试探索：当M，N在运动过程中，△M是否可能为等腰三角形？假设可能，那么求出相应的t值；假设不可能，说明理由．解答：解：〔1〕如图1，分别过A，D作AE⊥BC，DF⊥BC，分别交BC于E，F；..word.zl.\n..∴EF=AD=3；∵∠B=45°，AB=；∴BE=AE=DF=4．〔1分〕在Rt△DFC中，CF=；〔2分〕∴BC=BE+EF+CF=4+3+3=10；〔3分〕〔2〕①如图2，当0≤t≤5时，=BM=t，MC=10﹣t；过N作NG⊥于BC于点G；∴△NGC∽△DFC∴，即；∴NG=；∴S=；∵，函数开口向下；∴当时，Smax=10；〔5分〕②如图3，当5≤t≤8时，S=；∵﹣2＜0，即S随t的减小而增大；∴当t=5时，Smax=10；〔6分〕综上：，当t=5时，△M的面积S最大，最大值为10；〔3〕当0≤t≤5时：=BM=t，MC=10﹣t；①当MC=NC时，t=10﹣t，解得：t=5；〔7分〕②当HM=MC时，如图4，过N作NH⊥BC于点H，..word.zl.\n..那么有HC=MH，可得：，解得：；〔8分〕③当MN=MC时，如图5，过M作MI⊥CD于I，CI=，又，即：，可得，解得：〔舍去〕；〔9分〕当5＜t≤8时，如图6，过C作CJ⊥AD的延长线于点J，过N作NK⊥BC于点K；那么：MC2=〔10﹣t〕2=t2﹣20t+100；MN2=〔12﹣2t〕2+42=4t2﹣48t+160；NC2=〔t﹣2〕2+42=t2﹣4t+20；④当MC=NC时，t2﹣20t+100=t2﹣4t+20，解得：t=5〔舍去〕；〔10分〕⑤当MN=MC时，4t2﹣48t+160=t2﹣20t+100，解得：〔舍去〕；〔11分〕⑥当MN=NC时，t2﹣4t+20=4t2﹣48t+160，解得：〔舍去〕．〔12分〕综上：当时，△M为等腰三角形．..word.zl.