2021年初中数学中考100题压轴题精选 35页

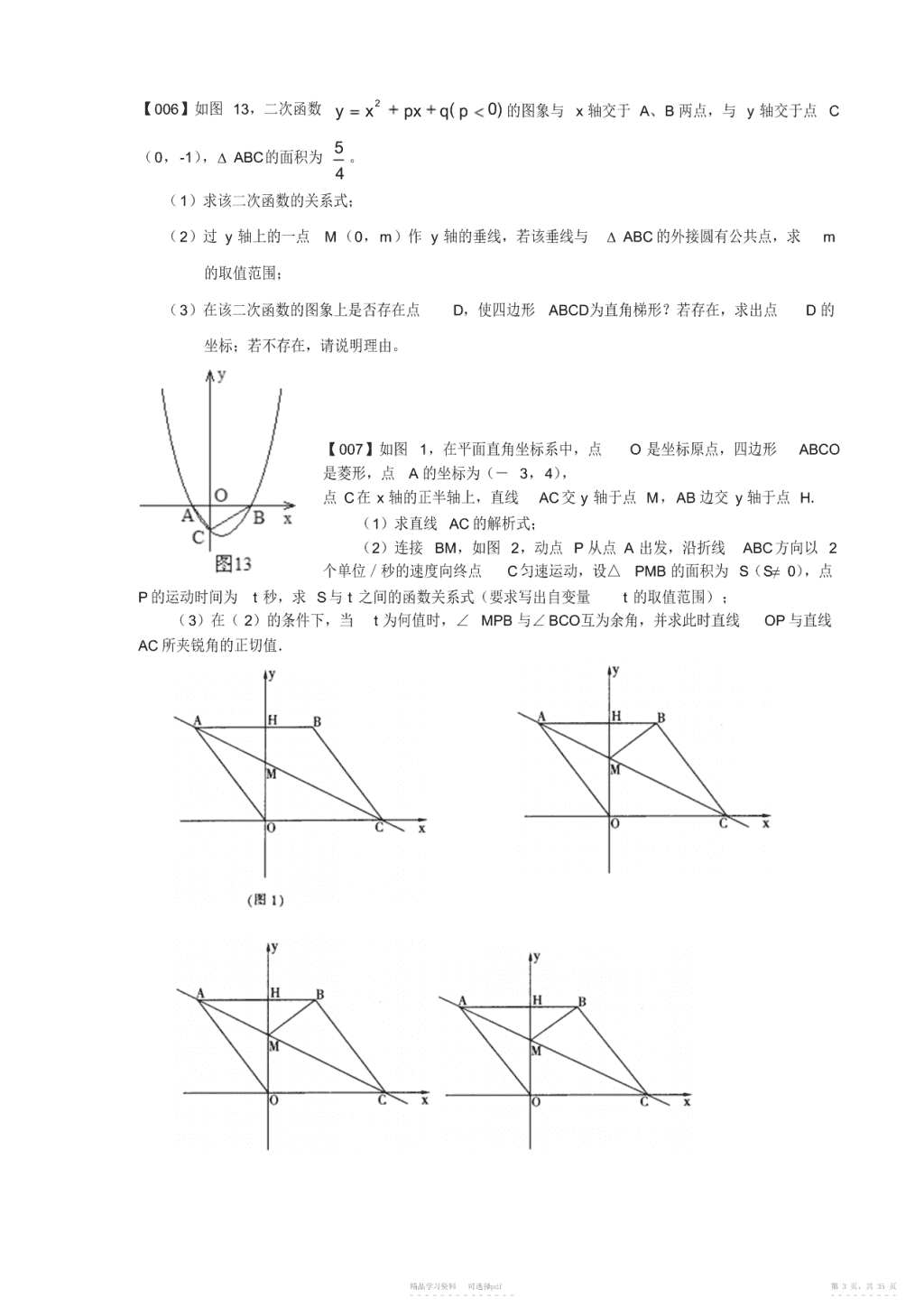
2011年中考数学压轴题100题精选2【001】如图，已知抛物线yax(1)33（a≠0）经过点A(2，0)，抛物线的顶点为D，过O作射线OM∥AD．过顶点D平行于x轴的直线交射线OM于点C，B在x轴正半轴上，连结BC．（1）求该抛物线的解析式；（2）若动点P从点O出发，以每秒1个长度单位的速度沿射线OM运动，设点P运动的时间为ts()．问当t为何值时，四边形DAOP分别为平行四边形？直角梯形？等腰梯形？（3）若OCOB，动点P和动点Q分别从点O和点B同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t()s，连接PQ，当t为何值时，四边形BCPQ的面积最小？并求出最小值及此时PQ的长．MyDCPAOQBx【002】如图16，在Rt△ABC中，∠C=90°，AC=3，AB=5．点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AC返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB-BC-CP于点E．点P、Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0）．B（1）当t=2时，AP=，点Q到AC的距离是；（2）在点P从C向A运动的过程中，求△APQ的面积S与t的函数关系式；（不必写出t的取值范围）（3）在点E从B向C运动的过程中，四边形QBED能否成EQ为直角梯形？若能，求t的值．若不能，请说明理由；（4）当DE经过点C时，请直接写出t的值．．．DACP图16【003】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）.2抛物线y=ax+bx过A、C两点.(1)直接写出点A的坐标，并求出抛物线的解析式；(2)动点P从点A出发．沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动．速度均为每秒1个单位长度，运动时间为t秒.过点P作PE⊥AB交AC于点E，①过精品学习资料可选择pdf第1页，共35页-----------------------\n点E作EF⊥AD于点F，交抛物线于点G.当t为何值时，线段EG最长?②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值。28【004】如图，已知直线l1:yx与直线l2:y2x16相交于点C，、l1l2分别交x轴于33AB、两点．矩形DEFG的顶点D、E分别在直线l1、l2上，顶点F、G都在x轴上，且点G与点B重合．（1）求△ABC的面积；（2）求矩形DEFG的边DE与EF的长；（3）若矩形DEFG从原点出发，沿x轴的反方向以每秒1个单位长度的速度平移，设移动时间为t(0≤≤t12)秒，矩形DEFG与△ABC重叠部分的面积为S，求S关t的函数关系式，并写出相应的t的取值范围．yl2l1EDCAOF（G）Bx（第26题）【005】如图1，在等腰梯形ABCD中，AD∥BC，E是AB的中点，过点E作EF∥BC交CD于点F．AB4，BC6，∠B60.（1）求点E到BC的距离；（2）点P为线段EF上的一个动点，过P作PMEF交BC于点M，过M作MN∥AB交折线ADC于点N，连结PN，设EPx.①当点N在线段AD上时（如图2），△PMN的形状是否发生改变？若不变，求出△PMN的周长；若改变，请说明理由；②当点N在线段DC上时（如图3），是否存在点P，使△PMN为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由.NADADADNPPEFEFEFBCBCBCMM图1图2图3AD（第25题）ADEFEFBCBC图4（备用）精品学习资料可选择pdf图5（备用）第2页，共35页-----------------------\n2【006】如图13，二次函数yxpxq(p)0的图象与x轴交于A、B两点，与y轴交于点C5（0，-1），ΔABC的面积为。4（1）求该二次函数的关系式；（2）过y轴上的一点M（0，m）作y轴的垂线，若该垂线与ΔABC的外接圆有公共点，求m的取值范围；（3）在该二次函数的图象上是否存在点D，使四边形ABCD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由。【007】如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（－3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H．（1）求直线AC的解析式；（2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；（3）在（2）的条件下，当t为何值时，∠MPB与∠BCO互为余角，并求此时直线OP与直线AC所夹锐角的正切值．精品学习资料可选择pdf第3页，共35页-----------------------\n【008】如图所示，在直角梯形ABCD中，∠ABC=90°，AD∥BC，AB=BC，E是AB的中点，CE⊥BD。（1）求证：BE=AD；（2）求证：AC是线段ED的垂直平分线；（3）△DBC是等腰三角形吗？并说明理由。【009】一次函数yaxb的图象分别与x轴、y轴交于点MN,，与k反比例函数y的图象相交于点,AB．过点A分别作ACx轴，AEy轴，垂足分别为CE,；x过点B分别作BFx轴，BDy轴，垂足分别为F，，DAC与BD交于点K，连接CD．k（1）若点AB，在反比例函数y的图象的同一分支上，如图1，试证明：x①SS；四边形AEDK四边形CFBK②ANBM．k（2）若点AB，分别在反比例函数y的图象的不同分支上，如图2，则AN与BM还相等x吗？试证明你的结论．yyNAx(1，y1)EEAx(1，y1)Bx(2，y2)NDKFMOCFMxOCxDKBx(3，y3)（图1）（图2）2【010】如图，抛物线yaxbx3与x轴交于AB，两点，与y轴交于C点，且经过点(2，3)a，对称轴是直线x1，顶点是M．（1）求抛物线对应的函数表达式；（2）经过C,M两点作直线与x轴交于点N，在抛物线上是否存在这样的点P，使以点PACN，，，为顶点的四边形为平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由；（3）设直线yx3与y轴的交点是D，在线段BD上任取一点E（不与BD，重合），经过ABE，，三点的圆交直线BC于点F，试判断△AEF的形状，并说明理由；（4）当E是直线yx3上任意一点时，（3）中的结论是否成立？（请直接写出结论）．yxAO1B3CM【011】已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为精品学习资料可选择pdf第4页，共35页-----------------------\nDF中点，连接EG，CG．（1）求证：EG=CG；（2）将图①中△BEF绕B点逆时针旋转45o，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）ADADADGFGEEFECCBCBFB①②③【012】如图，在平面直角坐标系xOy中，半径为1的圆的圆心O在坐标原点，且与两坐标轴分别2交于ABC、、、D四点．抛物线yaxbxc与y轴交于点D，与直线yx交于点M、N，且MA、NC分别与圆O相切于点A和点C．（1）求抛物线的解析式；（2）抛物线的对称轴交x轴于点E，连结DE，并延长DE交圆O于F，求EF的长．（3）过点B作圆O的切线交DC的延长线于点P，判断点P是否在抛物线上，说明理由．yDNEAOxCFMB【013】如图，抛物线经过A(40)，，B(10)，，C(0，2)三点．（1）求出抛物线的解析式；（2）P是抛物线上一动点，过P作PMx轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；（3）在直线AC上方的抛物线上有一点D，使得△DCA的面积最大，求出点D的坐标．yOB1Ax42C精品学习资料可选择pdf第5页，共35页-----------------------\n【014】在平面直角坐标中，边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点.现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线yx上时停止旋转，旋转过程中，AB边交直线yx于点M，BC边交x轴于点N（如图）.（1）求边OA在旋转过程中所扫过的面积；（2）旋转过程中，当MN和AC平行时，求正方形yOABC旋转的度数；yxA（3）设MBN的周长为p，在旋转正方形OABCM的过程中，p值是否有变化？请证明你的结论.BONxC【015】如图，二次函数的图象经过点D(0，73)，且(第26题)9顶点C的横坐标为4，该图象在x轴上截得的线段AB的长为6.⑴求二次函数的解析式；⑵在该抛物线的对称轴上找一点P，使PA+PD最小，求出点P的坐标；⑶在抛物线上是否存在点Q，使△QAB与△ABC相似？如果存在，求出点Q的坐标；如果不存在，请说明理由．【016】如图9，已知正比例函数和反比例函数的图象都经过点A(33)，．（1）求正比例函数和反比例函数的解析式；（2）把直线OA向下平移后与反比例函数的图象交于y点B(6，m)，求m的值和这个一次函数的解析式；A（3）第（2）问中的一次函数的图象与x轴、y轴分别交于C、D，求过A、3BB、D三点的二次函数的解析式；（4）在第（3）问的条件下，二次函数的图象上是否存在点E，使四边O3C6x2形OECD的面积S1与四边形OABD的面积S满足：S1S？若存在，求点3D精品学习资料可选择pdf第6页，共35页-----------------------\nE的坐标；若不存在，请说明理由．2【017】如图，已知抛物线yxbxc经过A(10)，，B(02)，两点，顶点为D．（1）求抛物线的解析式；（2）将△OAB绕点A顺时针旋转90°后，点B落到点C的位置，将抛物线沿y轴平移后经过点C，求平移后所得图象的函数关系式；（3）设（2）中平移后，所得抛物线与y轴的交点为B1，顶点为D1，若点N在平移后的抛物线上，且满足△NBB1的面积是△NDD1面积的2倍，求点N的坐标．yBOADx2018】如图，抛物线yaxbx4a经过A(10)，、C(04)，两点，与x轴交于另一点B．（1）求抛物线的解析式；（2）已知点Dm(，m1)在第一象限的抛物线上，求点D关于直线BC对称的点的坐标；（3）在（2）的条件下，连接BD，点P为抛物线上一点，且DBP45°，求点P的坐标．yCABxO【019】如图所示，将矩形OABC沿AE折叠，使点O恰好落在BC上F处，以CF为边作正方形CFGH，延长BC至M，使CM＝｜CF—EO｜，再以CM、CO为边作矩形CMNO(1)试比较EO、EC的大小，并说明理由S四边形CFGH(2)令m，请问m是否为定值？若是，请求出m的值；若不是，请说明理由S四边形CNMN；122(3)在(2)的条件下，若CO＝1，CE＝，Q为AE上一点且QF＝，抛物线y＝mx+bx+c经过C、Q33两点，请求出此抛物线的解析式.2(4)在(3)的条件下，若抛物线y＝mx+bx+c与线段AB交于点P，试问在直线BC上是否存在点K，精品学习资料可选择pdf第7页，共35页-----------------------\n使得以P、B、K为顶点的三角形与△AEF相似?若存在，请求直线KP与y轴的交点T的坐标?若不存在，请说明理由。【020】如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连结AD，以AD为一边且在AD的右侧作正方形ADEF。解答下列问题：（1）如果AB=AC，∠BAC=90°，①当点D在线段BC上时（与点B不重合），如图乙，线段CF、BD之间的位置关系为，数量关系为。②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，为什么？（2）如果AB≠AC，∠BAC≠90°点D在线段BC上运动。试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外）？画出相应图形，并说明理由。（画图不写作法）（3）若AC=42，BC=3，在（2）的条件下，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值。k1【021】如图，点P是双曲线y(k10，x0)上一动点，过点P作x轴、y轴的垂线，分别xk2交x轴、y轴于A、B两点，交双曲线y=（0＜k2＜|k1|）于E、F两点．x（1）图1中，四边形PEOF的面积S1=▲(用含k1、k2的式子表示)；（2）图2中，设P点坐标为（－4，3）．①判断EF与AB的位置关系，并证明你的结论；②记S2SPEFSOEF，S2是否有最小值？若有，求出其最小值；若没有，请说明理由。精品学习资料可选择pdf第8页，共35页-----------------------\n【022】一开口向上的抛物线与x轴交于A(m－2，0)，B(m＋2，0)两点，记抛物线顶点为C，且AC⊥BC．(1)若m为常数，求抛物线的解析式；(2)若m为小于0的常数，那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点？(3)设抛物线交y轴正半轴于D点，问是否存在实数m，使得△BCD为等腰三角形？若存在，求出m的值；若不存在，请说明理由．yDOABxC【023】如图，在梯形ABCD中，AD∥BC，AD2，BC4，点M是AD的中点，△MBC是等边三角形．（1）求证：梯形ABCD是等腰梯形；（2）动点P、Q分别在线段BC和MC上运动，且∠MPQ60保持不变．设PCx，MQy，求y与x的函数关系式；（3）在（2）中：①当动点P、Q运动到何处时，以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形？并指出符合条件的平行四边形的个数；②当y取最小值时，判断y△PQC的形状，并说明理由．BMADEQD60°QBCPAOPFCx23题24题【024】如图，已知ABC为直角三角形，ACB90，ACBC,点A、C在x轴上，点B坐标为（3，m）（m0），线段AB与y轴相交于点D，以P（1，0）为顶点的抛物线过点B、D．（1）求点A的坐标（用m表示）；（2）求抛物线的解析式；（3）设点Q为抛物线上点P至点B之间的一动点，连结PQ并延长交BC于点E，连结BQ并延长交AC于点F，试证明：FCAC(EC)为定值．【025】如图12，直线yx4与两坐标轴分别相交于A、B点，点M是线段AB上任意一点（A、B两点除外），过M分别作MC⊥OA于点C，MD⊥OB于D．精品学习资料可选择pdf第9页，共35页-----------------------\n（1）当点M在AB上运动时，你认为四边形OCMD的周长是否发生变化？并说明理由；（2）当点M运动到什么位置时，四边形OCMD的面积有最大值？最大值是多少？（3）当四边形OCMD为正方形时，将四边形OCMD沿着x轴的正方向移动，设平移的距离为a（0a)4，正方形OCMD与△AOB重叠部分的面积为S．试求S与a的函数关系式并画出该函数的图象．yyyBBBMDOCAxOAxOAx图12（1）图12（2）图12（3）【026】如图11，在△ABC中，∠C=90°，BC=8，AC=6，另有一直角梯形DEFH（HF∥DE，∠HDE=90°）的底边DE落在CB上，腰DH落在CA上，且DE=4，∠DEF=∠CBA，AH∶AC=2∶3（1）延长HF交AB于G，求△AHG的面积.（2）操作：固定△ABC，将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动，直到点D与点B重合时停止，设运动的时间为t秒，运动后的直角梯形为DEFH′（如图12）.探究1：在运动中，四边形CDH′H能否为正方形？若能，请求出此时t的值；若不能，请说明理由.探究2：在运动过程中，△ABC与直角梯形DEFH′重叠部分的面积为y，求y与t的函数关系.【027】阅读材料：如图12-1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得1出一种计算三角形面积的新方法：Sah，即三角形面积等于水平宽与铅垂高乘积的ABC2一半.解答下列问题：如图12-2，抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.(1)求抛物线和直线AB的解析式；(2)点P是抛物线(在第一象限内)上的一个动点，连结PA，PB，当P点运动到顶点C时，求△CAB的9铅垂高CD及SCAB；(3)是否存在一点P，使S△PAB=S△CAB，若存在,求出P点的坐标；若不存在，8请说明理由.yCBD1x精品学习资料可选择pdf第10页，共35页O1A-----------------------\n【028】如图，已知抛物线与x交于A(－1，0)、E(3，0)两点，与y轴交于点B(0，3)。（1）求抛物线的解析式；（2）设抛物线顶点为D，求四边形AEDB的面积；（3）△AOB与△DBE是否相似？如果相似，请给以证明；如果不相似，请说明理由。2【029】已知二次函数yxaxa2。（1）求证：不论a为何实数，此函数图象与x轴总有两个交点。（2）设a<0，当此函数图象与x轴的两个交点的距离为13时，求出此二次函数的解析式。（3）若此二次函数图象与x轴交于A、B两点，在函数图象上是否存在点P，使得△PAB的面积为313，若存在求出P点坐标，若不存在请说明理由。2【030】如图，已知射线DE与x轴和y轴分别交于点D(30)，和点E(04)，．动点C从点M(50)，出发，以1个单位长度/秒的速度沿x轴向左作匀速运动，与此同时，动点P从点D出发，也以1个单位长度/秒的速度沿射线DE的方向作匀速运动．设运动时间为t秒．（1）请用含t的代数式分别表示出点C与点P的坐标；1（2）以点C为圆心、t个单位长度为半径的⊙C与x轴交于A、B两点（点A在点B的左侧），2连接PA、PB．y①当⊙C与射线DE有公共点时，求t的取值范围；②当△PAB为等腰三角形时，求t的值．EPxODACBM【031】已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为(4,0)，(0,3).现有两动点P,Q分别从A,C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒.精品学习资料可选择pdf第11页，共35页-----------------------\n（1）填空：菱形ABCD的边长是▲、面积是▲、高BE的长是▲；（2）探究下列问题：①若点P的速度为每秒1个单位，点Q的速度为每秒2个单位.当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式，以及S的最大值；②若点P的速度为每秒1个单位，点Q的速度变为每秒k个单位，在运动过程中,任何时刻都有相应的k值，使得△APQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形.请探究当t=4秒时的情形，并求出k的值。yDEAOCxB【032】如图，已知A、B是线段MN上的两点，MN4，MA1，MB1．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使M、N两点重合成一点C，构成△ABC，设ABx．（1）求x的取值范围；（2）若△ABC为直角三角形，求x的值；（3）探究：△ABC的最大面积？CMABN21【033】已知抛物线yx2xa（a0）与y轴相交于点A，顶点为M.直线yxa分2别与x轴，y轴相交于B，C两点，并且与直线AM相交于点N.(1)填空：试用含a的代数式分别表示点M与N的坐标，则M，，N，；(2)如图，将△NAC沿y轴翻折，若点N的对应点N′恰好落在抛物线上，AN′与x轴交于点D，连结CD，求a的值和四边形ADCN的面积；精品学习资料可选择pdf第12页，共35页-----------------------\n2(3)在抛物线yx2xa（a0）上是否存在一点P，使得以P，，，ACN为顶点的四边形是平行四边形？若存在，求出P点的坐标；若不存在，试说明理由.yyCABCNN′NOxOBDxBBCA第（34）题AMM第（2）题备用图【034】若P为△ABC所在平面上一点，且APBBPCCPA120°，则点P叫做△ABC的费马点.（1）若点P为锐角△ABC的费马点，且ABC60°，PA3，PC4，则PB的值为________；（2）如图，在锐角△ABC外侧作等边△ACB′连结BB′.求证：BB′过△ABC的费马点P，且BB′=PAPBPC.【035】如图①，正方形ABCD中，点A、B的坐标分别为（0，10），（8，4），点C在第一象限．动点P在正方形ABCD的边上，从点A出发沿A→B→C→D匀速运动，同时动点Q以相同速度在x轴正半轴上运动，当P点到达D点时，两点同时停止运动，设运动的时间为t秒．(1)当P点在边AB上运动时，点Q的横坐标x（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；(2)求正方形边长及顶点C的坐标；(3)在（1）中当t为何值时，△OPQ的面积最大，并求此时P点的坐标；(4)如果点P、Q保持原速度不变，当点P沿A→B→C→D匀速运动时，OP与PQ能否相等，若能，写出所有符合条件的t的值；若不能，请说明理由．【036】已知：如图，在平面直角坐标系xOy中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=2，OC=3．过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E．（1）求过点E、D、C的抛物线的解析式；精品学习资料可选择pdf第13页，共35页-----------------------\n（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与y轴的正半轴交于点F，另一边与线段OC6交于点G．如果DF与（1）中的抛物线交于另一点M，点M的横坐标为，那么EF=2GO是否成立？5若成立，请给予证明；若不成立，请说明理由；（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．yDABExOC26题图1【037】已知平行于x轴的直线ya(a)0与函数yx和函数y的图像分别交于点A和点B，x又有定点P（2，0）.1（1）若a0，且tan∠POB=，求线段AB的长；（2）在过A，B两点且顶点在直线yx上9的抛物线中，已知线段8AB=，且在它的对称轴左边时，3y随着x的增大而增大，试求出满足条件的抛物线的解析式；（3）已知经过A，B，P三点的抛物线，平移后能得到92yx的图像，求点P到直5线AB的距离。【038】如图1，在平面直角坐标系中，O为坐标原点，点A的坐标为（－8，0），直线BC经过点B（－8，6），将四边形OABC绕点O按顺时针方向旋转α度得到四边形OA′B′C′，此时声母OA′、直线B′C′分别与直线BC相交于P、Q．（1）四边形的形状是，BP当α=90°时，的值是．PQBP（2）①如图2,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求的值;PQ②如图3,当四边形OA′B′C′的顶点B′落在直线BC上时,求ΔOPB′的面积．001（3）在四边形OABC旋转过程中,当0180时，是否存在这样的点P和点Q，使BP=BQ？2精品学习资料可选择pdf第14页，共35页-----------------------\n若存在，请直接写出点P的坐标；基不存在，请说明理由．2【039】如图，已知点A(-4，8)和点B(2，n)在抛物线yax上．(1)求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ+QB最短，求出点Q2的坐标；(2)平移抛物线yax，记平移后点A的对应点为A′，点B的对应点为B′，点C(-2，0)和点D(-4，0)是x轴上的两个定点．①当抛物线向左平移到某个位置时，A′C+CB′最短，求此时抛物线的函数解析式；②当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．【040】△ABC与△ABC是两个直角边都等于4厘米的等腰直角三角y形，M、N分别是直角边AC、BC的中点。△ABC位置固定，△ABC按A8如图叠放，使斜边AB在直线MN上,顶点B与点M重合。等腰直角△6ABC以1厘米/秒的速度沿直线MN向右平移，直到点A与点N重合。4设x秒时，△ABC与△ABC重叠部分面积为y平方厘米。2BDC3（1）当△ABC与△ABC重叠部分面积为2平方厘米时，求△-4-2O24x2-2-4ABC移动的时间；（2）求y与x的函数关系式；(第24题)（3）求△ABC与△ABC重叠部分面积的最大值。【041】某公交公司的公共汽车和出租车每天从乌鲁木y齐市出发往返于乌鲁木齐市和石河子市两地，出租车比1公共汽车多往返一趟，如图表示出租车距乌鲁木齐市的路程y（单位：千米）与所用时间x（单位：小时）的1函数图象．已知公共汽车比出租车晚1小时出发，到达石河子市后休息2小时，然后按原路原速返回，结果比5出租车最后一次返回乌鲁木齐早1小时．请在图中画出公共汽车距乌鲁木齐市的路程y（1）千米）与所用时间x（小时）的函数图象．012345678x精品学习资料可选择pdf第15页，共35页-----------------------\n（2）求两车在途中相遇的次数（直接写出答案）（3）求两车最后一次相遇时，距乌鲁木齐市的路程．【042】如图9，在矩形OABC中，已知A、C两点的坐标分别为A(40)，、C(02)，，D为OA的y中点．设点P是AOC平分线上的一个动点（不与点O重合）．（1）试证明：无论点P运动到何处，PC总与PD相等；C(02)，B（2）当点P运动到与点B的距离最小时，试确定过OPD、、三点的抛物线的解析式；P（3）设点E是（2）中所确定抛物线的顶点，当点P运动到何ODA(40)，x处时，△PDE的周长最小？求出此时点P的坐标和△PDE的周长；图9（4）设点N是矩形OABC的对称中心，是否存在点P，使CPN90°？若存在，请直接写出点P的坐标．2【043】已知函数y1x，y2xbxc，，为方程y1y20的两个根，点M1，T在函数y2的图象上．11（Ⅰ）若，，求函数y2的解析式；321（Ⅱ）在（Ⅰ）的条件下，若函数y1与y2的图象的两个交点为AB，，当△ABM的面积为12时，求t的值；（Ⅲ）若01，当0t1时，试确定T，，三者之间的大小关系，并说明理由．12【044】如图9，已知抛物线y=x–2x＋1的顶点为P，A为抛物线与y轴的交点，过A与y轴垂2直的直线与抛物线的另一交点为B，与抛物线对称轴交于点O′，过点B和P的直线l交y轴于点C，连结O′C，将△ACO′沿O′C翻折后，点A落在点D的位置．(1)求直线l的函数解析式；(2)求点D的坐标；(3)抛物线上是否存在点Q，使得S△DQC=S△DPB?若存在，求出所有符合条件的点Q的坐标；若不存在，请说明理由．1045】如图，已知直线yx1与y轴交于点A，与x轴交于点D，212抛物线yxbxc与直线交于A、E两点，与x轴交于B、C两2点，且B点坐标为(1，0)。⑴求该抛物线的解析式；⑵动点P在轴上移动，当△PAE是直角三角形时，求点P的坐标P。⑶在抛物线的对称轴上找一点M，使|AMMC|的值最大，求出点图9M的坐标。精品学习资料可选择pdf第16页，共35页-----------------------\n28【046】如图，已知直线l1:yx与直线l2:y2x16相交于点C，、l1l2分别交x轴于33AB、两点．矩形DEFG的顶点D、E分别在直线l1、l2上，顶点F、G都在x轴上，且点G与点B重合．（1）求△ABC的面积；（2）求矩形DEFG的边DE与EF的长；（3）若矩形DEFG从原点出发，沿x轴的反方向以每秒1个单位长度的速度平移，设移动时间为t(0≤≤t12)秒，矩形DEFG与△ABC重叠部分的面积为S，求S关于t的函数关系式，并写出相应的t的取值范围．yl2l1EDCAOF（G）Bx【047】如图（1），将正方形纸片ABCD折叠，使点B落在CD边上一点E（不与点C，D重合），CE1AM压平后得到折痕MN．当时，求的值．CD2BN方法指导：AM为了求得的值，可先求BN、AM的长，不妨设：AB=2BN类比归纳CE1AMCE1AM在图（1）中，若，则的值等于；若，则的值等CD3BNCD4BNCE1AM于；若（n为整数），则的值等于．（用含n的式子表示）CDnBN联系拓广如图（2），将矩形纸片ABCD折叠，使点B落在CD边上一点E（不与点C，D重合），压平AB1CE1AM后得到折痕MN，设m1，，则的值等于．（用含m，n的式子表BCmCDnBN示）FFAMDMADEEBCBCNN图（2）图（1）精品学习资料可选择pdf第17页，共35页-----------------------\n【048】如图11，抛物线ya(x3)(x)1与x轴相交于A、B两点（点A在点B右侧），过点A的直线交抛物线于另一点C，点C的坐标为（-2，6）.(1)求a的值及直线AC的函数关系式；(2)P是线段AC上一动点，过点P作y轴的平行线，交抛物线于点M，交x轴于点N.①求线段PM长度的最大值；②在抛物线上是否存在这样的点M，使得△CMP与△APN相似？如果存在，请直接写出所有满足条件的点M的坐标（不必写解答过程）；如果不存在，请说明理由。2【049】已知：抛物线yaxbxca0的对称轴为x1，与x轴交于AB，两点，与y轴交于点C，其中A30，、C0，2．（1）求这条抛物线的函数表达式．（2）已知在对称轴上存在一点P，使得△PBC的周长最小．请求出点P的坐标．（3）若点D是线段OC上的一个动点（不与点O、点C重合）．过点D作DE∥PC交x轴于点E．连接PD、PE．设CD的长为m，△PDE的面积为S．求S与m之间的函数关系式．试说明S是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．yAEDQAOBPxBCF50题C【050】如图，在梯形ABCD中，AD∥BC，AD6cm，CD4cm，BCBD10cm，点P由B出发沿BD方向匀速运动，速度为1cm/s；同时，线段EF由DC出发沿DA方向匀速运动，速度为1cm/s，交BD于Q，连接PE．若设运动时间为t（s）（0t5）．解答下列问题：（1）当t为何值时，PE∥AB？2（2）设△PEQ的面积为y（cm），求y与t之间的函数关系式；2（3）是否存在某一时刻t，使S△PEQS△BCD？若存在，求出此时t的值；若不存在，说明理由．25（4）连接PF，在上述运动过程中，五边形PFCDE的面积是否发生变化？说明理由．2【051】如图14（1），抛物线yx2xk与x轴交于A、B两点，与y轴交于点C（0，3）．［图14（2）、图14（3）为解答备用图］精品学习资料可选择pdf第18页，共35页-----------------------\n（1）k，点A的坐标为，点B的坐标为；2（2）设抛物线yx2xk的顶点为M，求四边形ABMC的面积；（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；2（4）在抛物线yx2xk上求点Q，使△BCQ是以BC为直角边的直角三角形．图14（1）图14（2）图14（3）2【052】已知二次函数yaxbxc（a0）的图象经过点A(10)，，B(20)，，C(0，2)，直线xm（m2）与x轴交于点D．（1）求二次函数的解析式；（2）在直线xm（m2）上有一点E（点E在第四象限），使得E、、DB为顶点的三角形与以AO、、C为顶点的三角形相似，求E点坐标（用含m的代数式表示）；（3）在（2）成立的条件下，抛物线上是否存在一点F，使得四边形ABEF为平行四边形？若存在，请求出m的值及四边形ABEF的面积；若不存在，请说明理由．yOx2【053】如图所示，在平面直角坐标系中，抛物线yaxbxc（a0）经过A(10)，，B(30)，，C(03)，三点，其顶点为D，连接BD，点P是线段BD上一个动点（不与B、D重合），过点P作yDy轴的垂线，垂足为E，连接BE．C32（1）求抛物线的解析式，并写出顶点D的坐标；EP1AB（2）如果P点的坐标为(x，y)，△PBE的面积为s，求s与x321O123x1的函数关系式，写出自变量x的取值范围，并求出s的最大值；（3）在（2）的条件下，当s取得最大值时，过点P作x的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为P，请直接写出P点坐标，并判断点P是否在该抛物线上．【054】如图，在直角坐标系中，矩形ABCD的边AD在y轴正半轴上，点A、C的坐标分别为（0，1）、（2，4）．点P从点A出发，沿A→B→C以每秒1个单位的速度运动，到精品学习资料可选择pdf第19页，共35页-----------------------\n12点C停止；点Q在x轴上，横坐标为点P的横、纵坐标之和．抛物线yxbxc4经过A、C两点．过点P作x轴的垂线，垂足为M，交抛物线于点R．设点P的运动时间为t（秒），△PQR的面积为S（平方单位）．（1）求抛物线对应的函数关系式．（2）分别求t=1和t=4时，点Q的坐标．（3）当0＜t≤5时，求S与t之间的函数关系式，并直接写出S的最大值．【055】在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，2且点A(02)，，点C(10)，，如图所示：抛物线yaxax2经过点B．（1）求点B的坐标；y（2）求抛物线的解析式；（3）在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在，请说明理由．ByAPA（0，2）BODCxC（－1，0）x图56（第25题）2【056】如图18，抛物线F：yaxbxc的顶点为P，抛物线：与y轴交于点A，与直线OP交于点B．过点P作PD⊥x轴于点D，平移抛物线F使其经过点2A、D得到抛物线F′：yaxbxc，抛物线F′与x轴的另B、一个交点为C．⑴当a=1，b=－2，c=3时，求点C的坐标(直接写出答案)；2⑵若a、b、c满足了b2ac①求b：b′的值；精品学习资料可选择pdf第20页，共35页-----------------------\n②探究四边形OABC的形状，并说明理由．【057】直线ykxb(k)0与坐标轴分别交于A、B两点，OA、OB的长分别是方程2x14x480的两根（OAOB），动点P从O点出发，沿路线O→B→A以每秒1个单位长度的速度运动，到达A点时运动停止．（1）直接写出A、B两点的坐标；（2）设点P的运动时间为t(秒)，OPA的面积为S，求S与t之间的函数关系式（不必写出自变量的取值范围）；（3）当S12时，直接写出点P的坐标，此时，在坐标轴上是否存在点M，使以O、A、P、M为顶点的四边形是梯形？若存在，请直接写出点M的坐标；若不存在，请说明理由．yyBPPOAxAoBxC58题2【058】如图，已知抛物线yx1与x轴交于A、B两点，与y轴交于点C．（1）求A、B、C三点的坐标．（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．（3）在x轴上方的抛物线上是否存在一点M，过M作MGx轴于点G，使以A、M、G三点为顶点的三角形与PCA相似．若存在，请求出M点的坐标；否则，请说明理由．【059】如图（1），已知正方形ABCD在直线MN的上方，BC在直线MN上，E是BC上一点，以AE为边在直线MN的上方作正方形AEFG．（1）连接GD，求证：△ADG≌△ABE；(4分)（2）连接FC，观察并猜测∠FCN的度数，并说明理由；(4分)（3）如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=a，BC=b（a、b为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变，若∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请举例说明．(5分)GGDADFFMECNMBECNB图（1）图（2）精品学习资料可选择pdf第21页，共35页-----------------------\n2【060】已知：如图所示，关于x的抛物线yaxxca(0)与x轴交于点A(20)，、点B(60)，，与y轴交于点C．（1）求出此抛物线的解析式，并写出顶点坐标；（2）在抛物线上有一点D，使四边形ABDC为等腰梯形，写出点D的坐标，并求出直线AD的解析式；（3）在（2）中的直线AD交抛物线的对称轴于点M，抛物线上有一动点P，x轴上有一动点Q．是否存在以A、M、、PQ为顶点的平行四边形？如果存在，请直接写出点Q的坐标；如果不存在，yC请说明理由．AOBx（第26题图）3【061】如图已知直线L：yx3，它与x轴、y轴的交点分别为A、B两点。4（1）求点A、点B的坐标。（2）设F为x轴上一动点，用尺规作图作出⊙P，使⊙P经过点B且与x轴相切于点F（不写作法，保留作图痕迹）。（3）设92）中所作的⊙P的圆心坐标为P（x，y），求y关于x的函数关系式。（4）是否存在这样的⊙P，既与x轴相切又与直线L相切于点B，若存在，求出圆心P的坐标，若不存在，请说明理由。精品学习资料可选择pdf第22页，共35页-----------------------\n【062】如图13-1至图13-5，⊙O均作无滑动滚动，⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置，⊙O的周长为c．O1OO2阅读理解：（1）如图13-1，⊙O从⊙O1的位置出发，沿AB滚动到AB⊙O2的位置，当AB=c时，⊙O恰好自转1周．图13-1（2）如图13-2，∠ABC相邻的补角是n°，⊙O在O1∠ABC外部沿A-B-C滚动，在点B处，必须由O2⊙O1的位置旋转到⊙O2的位置，⊙O绕点B旋ABn°DnC转的角∠O1BO2=n°，⊙O在点B处自转周．图13-2360实践应用：（1）在阅读理解的（1）中，若AB=2c，则⊙O自转周；若AB=l，则⊙O自转周．在O1OO2阅读理解的（2）中，若∠ABC=120°，则⊙OO3AB在点B处自转周；若∠ABC=60°，则⊙O在点B处自转周．1CO4（2）如图13-3，∠ABC=90°，AB=BC=c．⊙O从2图13-3⊙O1的位置出发，在∠ABC外部沿A-B-C滚动到⊙O4的位置，⊙O自转周．拓展联想：B（1）如图13-4，△ABC的周长为l，⊙O从与AB相切于点D的位置出发，在△ABC外部，按顺时针方向沿三角形滚O动，又回到与AB相切于点D的位置，⊙O自转了多少D周？请说明理由．AC图13-4（2）如图13-5，多边形的周长为l，⊙O从与某边相切于点D的位置出发，在多边形外部，按顺时针方向沿多边形滚动，又回到与该边相切于点D的位置，直接写．．出⊙O自转的周数．ODy2【063】如图12，已知抛物线yx4x3交x轴于A、B两点，图13-5交y轴于点C，?抛物线的对称轴交x轴于点E，点B的C坐标为（1，0）．（1）求抛物线的对称轴及点A的坐标；D（2）在平面直角坐标系xoy中是否存在点P，与A、B、C三点构成一个平行四边形？AEBOx若存在，请写出点P的坐标；若不存在，请说明理由；图12精品学习资料可选择pdf第23页，共35页-----------------------\n（4）连结CA与抛物线的对称轴交于点D，在抛物线上是否存在点M，使得直线CM把四边形DEOC分成面积相等的两部分？若存在，请求出直线CM的y解析式；若不存在，请说明理由．A·B12【064】如图，抛物线yxx2的顶点为A，与y轴交于点B．4（1）求点A、点B的坐标．Ox（2）若点P是x轴上任意一点，求证：PAPB≤AB．（3）当PAPB最大时，求点P的坐标．【065】如图11，AB是⊙O的直径，弦BC=2cm，∠ABC=60o．第64题图（1）求⊙O的直径；（2）若D是AB延长线上一点，连结CD，当BD长为多少时，CD与⊙O相切；（3）若动点E以2cm/s的速度从A点出发沿着AB方向运动，同时动点F以1cm/s的速度从B点出发沿BC方向运动，设运动时间为t(s)(0t)2，连结EF，当t为何值时，△BEF为直角三角形．CCCFFEAABABOBDOOE图10（1）图10（2）图10（3）m15【066】如图，反比例函数y＝(x＞0)的图象与一次函数y＝－x＋的图象交于A、B两点，点Cx221的坐标为(1，)，连接AC，AC∥y轴．2(1)求反比例函数的解析式及点B的坐标；(2)现有一个直角三角板，让它的直角顶点P在反比例函数图象上A、B之间的部分滑动(不与A、B重合)，两直角边始终分别平行于x轴、y轴，且与线段AB交于M、N两点，试判断P点在滑动过程中△PMN是否与△CBA总相似？简要说明判断理由．APDOBCQ67题精品学习资料可选择pdf第24页，共35页-----------------------\n【067】如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90o，AB＝12cm，AD＝8cm，BC＝22cm，AB为⊙O的直径，动点P从点A开始沿AD边向点D以1cm/s的速度运动，动点Q从点C开始沿CB边向点B以2cm/s的速度运动，P、Q分别从点A、C同时出发，当其中一点到达端点时，另一个动点也随之停止运动．设运动时间为t(s)．(1)当t为何值时，四边形PQCD为平行四边形？(2)当t为何值时，PQ与⊙O相切？【068】如图12，在直角梯形OABC中，OA∥CB，A、B两点的坐标分别为A（15，0），B（10，12），动点P、Q分别从O、B两点出发，点P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q也同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交x轴于点F．设动点P、Q运动时间为t（单位：秒）．（1）当t为何值时，四边形PABQ是等腰梯形，请写出推理过程；（2）当t=2秒时，求梯形OFBC的面积；（3）当t为何值时，△PQF是等腰三角形？请写出推理过程．22【069】如图11，已知二次函数y(xm)km的图象与x轴相交于两个不同的点Ax(1，0)、Bx(2，0)，与y轴的交点为C．设△ABC的外接圆的圆心为点P．（1）求⊙P与y轴的另一个交点D的坐标；（2）如果AB恰好为⊙P的直径，且△ABC的面积等于5，求m和k的值．【070】如图所示，菱形ABCD的边长为6厘米，B60°．从初始时刻开始，点P、Q同时从A点出发，点P以1厘米/秒的速度沿ACB的方向运动，点Q以2厘米/秒的速度沿ABCD的方向运动，当点Q运动到D点时，P、Q两点同时停止运动，设P、Q运动的时间为x秒时，△APQ与△ABC重叠部分的面积为y平方厘米（这里规定：点和线段是面．．．．积为O的三角形），解答下列问题：（1）点P、Q从出发到相遇所用时间是秒；（2）点P、Q从开始运动到停止的过程中，当△APQ是等边三角形时x的值是秒；yAOBx精品学习资料可选择pdf第25页，共35页-----------------------\n（3）求y与x之间的函数关系式．CDPBAQ（第70题）2【071】已知：抛物线yaxbxca0的对称轴为x1，与x轴交于AB，两点，与y轴交于点C，其中A30，、C0，2．（1）求这条抛物线的函数表达式．（2）已知在对称轴上存在一点P，使得△PBC的周长最小．请求出点P的坐标．（3）若点D是线段OC上的一个动点（不与点O、点C重合）．过点D作DE∥PC交x轴于点E．连接PD、PE．设CD的长为m，△PDE的面积为S．求S与m之间的函数关系式．试说明S是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．【072】如图1所示，直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l．将直线l平移，平移后的直线l与x轴交于点D，与y轴交于点E．（1）将直线l向右平移，设平移距离CD为t(t0)，直角梯形OABC被直线l扫过的面积（图中阴影部份）为s，s关于t的函数图象如图2所示，OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．①求梯形上底AB的长及直角梯形OABC的面积；②当2t4时，求S关于t的函数解析式；（2）在第（1）题的条件下，当直线l向左或向右平移时（包括l与直线BC重合），在直线AB上．．．．是否存在点P，使PDE为等腰直角三角形?若存在，请直接写出所有满足条件的点P的坐标;若不存在，请说明理由．【073】)如图，半径为25的⊙O内有互相垂直的两条弦AB、CD相交于P点．(1)求证：PA·PB=PC·PD；(2)设BC的中点为F，连结FP并延长交AD于E，求证：EF⊥AD：(3)若AB=8，CD=6，求OP的长．精品学习资料可选择pdf第26页，共35页-----------------------\nCFPABEOD第23题图【074】如图，在平面直角坐标系中，点O1的坐标为(40)，，以点O1为圆心，8为半径的圆与x轴交于AB，两点，过A作直线l与x轴负方向相交成60°的角，且交y轴于C点，以点O2(135)，为圆心的圆与x轴相切于点D．（1）求直线l的解析式；（2）将⊙O2以每秒1个单位的速度沿x轴向左平移，当⊙O2第一次与⊙O1外切时，求⊙O2平移yy的时间．lO260°O1AOBDxBOAxCC（第74题）D75题2075】如图11，已知抛物线yax2axb（a0）与x轴的一个交点为B(10)，，与y轴的负半轴交于点C，顶点为D．（1）直接写出抛物线的对称轴，及抛物线与x轴的另一个交点A的坐标；（2）以AD为直径的圆经过点C．①求抛物线的解析式；②点E在抛物线的对称轴上，点F在抛物线上，且以B，A，F，E四点为顶点的四边形为平行四边形，求点F的坐标．12【076】如图，抛物线yxmxn与x轴交于A、B两点，与y轴交于C点，四边形OBHC为2矩形，CH的延长线交抛物线于点D（5，2），连结BC、AD.（1）求C点的坐标及抛物线的解析式；（2）将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；（3）设过点E的直线交AB边于点P，交CD边于点Q.问是否存在点P，使直线PQ分梯形ABCD的面积为1∶3两部分？若存在，求出P点坐标；若不存在，请说明理由.精品学习资料可选择pdf第27页，共35页-----------------------\n3【077】已知直线yxm与x轴y轴分别交于点A和点B，点B的坐标为（0，6）4（1）求的m值和点A的坐标；（2）在矩形OACB中，点P是线段BC上的一动点，直线PD⊥AB于点D，与x轴交于点E，设BP=a，梯形PEAC的面积为s。①求s与a的函数关系式，并写出a的取值范围；②⊙Q是△OAB的内切圆，求当PE与⊙Q相交的弦长为2.4时点P的坐标。【078】如图12，已知直线L过点A(01)，和B(10)，，P是x轴BPC正半轴上的动点，OP的垂直平分线交L于点Q，交x轴于QD点M．OEA（1）直接写出直线L的解析式；（2）设OPt，△OPQ的面积为S，求S关于t的函数关系式；并求出当0t2时，S的最大值；（3）直线L1过点A且与x轴平行，问在L1上是否存在点C，使得△CPQ是以Q为直角顶点的等腰直角三角形？若存在，求出点C的坐标，并证明；若不存在，请说明理由．yyLL1ADAQxOMPBBOCx图1279题图【079】如图，ABCD在平面直角坐标系中，AD6，若OA、OB的长是关于x的一元二次方2程x7x120的两个根，且OAOB．16（1）求sinABC的值．（2）若E为x轴上的点，且S△AOE，求经过D、E两3点的直线的解析式，并判断△AOE与△DAO是否相似？（3）若点M在平面直角坐标系内在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，请直接写出F点的坐标；若不存在，请说明理由．【080】已知：等边三角形ABC的边长为4厘米，长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动（运动开始时，点M与点A重合，点N到达点B时运动终止），过点M、N分别作AB边的垂线，与△ABC的其它边交于P、Q两点，线段MN运动的时间为t秒．（1）线段MN在运动的过程中，t为何值时，四边形MNQP恰为矩形？并求出该矩形的面积；（2）线段MN在运动的过程中，四边形MNQP的面积为S，运动的时间为t．求四边形MNQP的面积S随运动时间t变化的函数关系式，并写出自变量t的取值范围．精品学习资料可选择pdf第28页，共35页-----------------------\nCyQHQAOBxP81题PCAMNB32【081】如图，已知抛物线y＝x＋bx＋c与坐标轴交于A、B、43C三点，A点的坐标为（－1，0），过点C的直线y＝x－3与x轴交于点Q，点P是线段BC4t上的一个动点，过P作PH⊥OB于点H．若PB＝5t，且0＜t＜1．（1）填空：点C的坐标是_▲_，b＝_▲_，c＝_▲_；（2）求线段QH的长（用含t的式子表示）；（3）依点P的变化，是否存在t的值，使以P、H、Q为顶点的三角形与△COQ相似？若存在，求出所有t的值；若不存在，说明理由．【082】（09上海）在直角坐标平面内，O为原点，点A的坐标为(10)，，点C的坐标为(04)，，直线CM∥x轴（如图7所示）．点B与点A关于原点对称，直线yxb（b为常数）经过点B，且与直线CM相交于点D，联结OD．（1）求b的值和点D的坐标；yyxb（2）设点P在x轴的正半轴上，若△POD是等腰三角形，求点P的坐标；4CDM（3）在（2）的条件下，如果以PD为半径的圆P与3圆O外切，求圆O的半径．2【083】如图，在直角坐标系中，点A的坐标为（－2，1BA0），连结OA，将线段OA绕原点O顺时针旋转120°，x得到线段OB.1O1（1）求点B的坐标；（2）求经过A、O、B三点的抛物线的解析式；82题（3）在（2）中抛物线的对称轴上是否存在点C，使△BOC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由.（4）如果点P是（2）中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由.y【084】如图，在平面直角坐标系中，直线l：y=－2x－8分别与x轴，y轴相交于A，B两点，点P（0，k）是y轴的负半轴上的B一个动点，以P为圆心，3为半径作⊙P.（1）连结PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；（2）当k为何值时，以⊙P与直线lAOx的两个交点和圆心P为顶点的三角形是正三角形？83题精品学习资料可选择pdf第29页，共35页-----------------------\n84题2【085】如图①，已知抛物线yaxbx3（a≠0）与x轴交于点A(1，0)和点B(－3，0)，与y轴交于点C．(1)求抛物线的解析式；(2)设抛物线的对称轴与x轴交于点M，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．(3)如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．【086】如图，以BC为直径的⊙O交△CFB的边CF于点A，BM平分23∠ABC交AC于点M，AD⊥BC于点D，AD交BM于点N，ME⊥BC于点E，AB=AF·AC，cos∠ABD=，5AD=12．⑴求证：△ANM≌△ENM；⑵求证：FB是⊙O的切线；⑶证明四边形AMEN是菱形，并求该菱形的面积S．2【087】如图，已知抛物线y＝x＋bx＋c经过矩形ABCD的两个顶点A、B，AB平行于x轴，对角线3BD与抛物线交于点P，点A的坐标为(0，2)，AB＝4．1)求抛物线的解析式；(2)若S△APO＝，求矩2y形ABCD的面积．yAB2xABO1QPCOP13xDC第88题图(第87题图)精品学习资料可选择pdf第30页，共35页-----------------------\n【088】如图所示，已知在直角梯形OABC中，AB∥OC，BC⊥x轴于点C，A(11)，、B(31)，．动点P从O点出发，沿x轴正方向以每秒1个单位长度的速度移动．过P点作PQ垂直于直线，．．OA垂足为Q．设P点移动的时间为t秒（0t4），△OPQ与直角梯形OABC重叠部分的面积为S．（1）求经过O、、AB三点的抛物线解析式；（2）求S与t的函数关系式；（3）将△OPQ绕着点P顺时针旋转90°，是否存在t，使得△OPQ的顶点O或Q在抛物线上？若存在，直接写出t的值；若不存在，请说明理由．【089】如图，在平面直角坐标系xOy中，半径为1的圆的圆心O在坐标原点，且与两坐标轴分别2交于ABC、、、D四点．抛物线yaxbxc与y轴交于点D，与直线yx交于点M、N，且MA、NC分别与圆O相切于点A和点C．（1）求抛物线的解析式；（2）抛物线的对称轴交x轴于点E，连结DE，并延长DE交圆O于F，求EF的长．（3）过点B作圆O的切线交DC的延长线于点P，判断点P是否在抛物线上，说明理由．yyyDNEGAOBxAOFBxEAOCxQDCMFMNBy=kx+1图（9）-1图（9）-22【090】如图（9）-1，抛物线yax3axb经过A（1，0），C（3，2）两点，与y轴交于点D，与x轴交于另一点B．（1）求此抛物线的解析式；（2）若直线ykx(1k)0将四边形ABCD面积二等分，求k的值；（3）如图（9）-2，过点E（1，1）作EF⊥x轴于点F，将△AEF绕平面内某点旋转180°得△MNQ（点M、N、Q分别与点A、E、F对应），使点M、N在抛物线上，作MG⊥x轴于点G，若线段MG︰AG＝1︰2，求点M，N的坐标．2【091】已知二次函数y＝x－x＋c．2(1)若点A(－1，a)、B(2，2n－1)在二次函数y＝x－x＋c的图象上，求此二次函数的最小值；2(2)若点D(x1，y1)、E(x2，y2)、P(m，n)(m＞n)在二次函数y＝x－x＋c的图象上，且D、E两点关于坐标原点成中心对称，连接OP．当22≤OP≤2＋2时，试判断直线DE与抛物23线y＝x－x＋c＋的交点个数，并说明理由．8精品学习资料可选择pdf第31页，共35页-----------------------\n372【092】已知：直角梯形OABC的四个顶点是O(0，0)，A(，1)，B(s，t)，C(，0)，抛物线y=x22＋mx－m的顶点P是直角梯形OABC内部或边上的一个动点，m为常数．(1)求s与t的值，并在直角坐标系中画出．．直角梯形OABC；2(2)当抛物线y=x＋mx－m与直角梯形OABC的边AB相交时，求m的取值范围．y321-1O12345x-1（第24题）【093】已知在平面直角坐标系中，四边形OABC是矩形，点A、C的坐标分别为A3，、C04，，点D的坐标为D5，，点P是直线AC上的一动点，直线DP与y轴交于点M．问：（1）当点P运动到何位置时，直线DP平分矩形OABC的面积，请简要说明理由，并求出此时直线DP的函数解析式；（2）当点P沿直线AC移动时，是否存在使△DOM与△ABC相似的点M，若存在，请求出点M的坐标；若不存在，请说明理由；（3）当点P沿直线AC移动时，以点P为圆心、半径长为R（R＞0）画圆，所得到的圆称为动圆P．若设动圆P的直径长为AC，过点D作动圆P的两条切线，切点分别为点E、F．请探求是否存在四边形DEPF的最小面积S，若存在，请求出S的值；若不存在，请说明理由．注：第（3）问请用备用图解答．yyCBCBDOAxDOAx备用图精品学习资料可选择pdf第32页，共35页-----------------------\n【094】在平面直角坐标系中，已知A(40)，，B(10)，，且以AB为直径的圆交y轴的正半轴于点C(02)，，过点C作圆的切线交x轴于点D．（1）求过ABC，，三点的抛物线的解析式（2）求点D的坐标（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与xy轴相切？若存在，求出该圆的半径，若不存在，请说明理由？12【095】）如图1，已知：抛物线yxbxc与C22x轴交于AB、两点，与y轴交于点C，经过BC、ABD4O1x1两点的直线是yx2，连结AC．2（1）B、C两点坐标分别为B（_____，_____）、C（_____，_____），抛物线的函数关系式为______________；（2）判断△ABC的形状，并说明理由；3）若△ABC内部能否截出面积最大的矩形DEFC（顶点D、、、EFG在△ABC各边上）？若能，求出在AB边上的矩形顶点的坐标；若不能，请说明理由．yyAOBxAOBxCC图1图2(备用)（第26题）【096】如图12，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为(2,4)；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3.（1）求该抛物线所对应的函数关系式；（2）将矩形ABCD以每秒1个单位长度的速度从图12所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t．．．．．≤3），直线AB与该抛物线的交点为N（如图13所示）.5①当t=时，判断点P是否在直线ME上，并说明理由；2②设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．yyMMNCBCB·PDO(A)ExDOAEx精品学习资料可选择pdf第33页，共35页图12--------------图13---------\n【097】矩形OABC在平面直角坐标系中位置如图13所示，AC、两点的坐标分别为A(60)，，3C(0，3)，直线yx与BC边相交于D点．4（1）求点D的坐标；29（2）若抛物线yaxx经过点A，试确定此抛物线的表达式；4（3）设（2）中的抛物线的对称轴与直线OD交于点M，点P为对称轴上一动点，以PO、、M为顶点的三角形与△OCD相似，求符合条件的点P的坐标．yAO6x3BCD3yx4图13【098】如图，在平面直角坐标系中，点A（0，6），点B是x轴上的一个动点，连结AB，取AB的o中点M，将线段MB绕着点B按顺时针方向旋转90，得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是（t，0）.（1）当t=4时，求直线AB的解析式；（2）当t>0时，用含t的代数式表示点C的坐标及△ABC的面积；（3）是否存在点B,使△ABD为等腰三角形?若存在，请求出所有符合条件的点B的坐标；若不存在，请说明理由.yyAA·DCMOBxOx备用图【099】我们所学的几何知识可以理解为对“构图”的研究：根据给定的（或构造的）几何图形提．．．．．．．．．．．．．．．．出相关的概念和问题（或者根据问题构造图形），并加以研究.．．．．．．．．．．．．．．．．．．．．．．．．．．．例如：在平面上根据两条直线的各种构图，可以提出“两条直线平行”、“两条直线相交”的概念；若增加第三条直线，则可以提出并研究“两条直线平行的判定和性质”等问题（包括研究的思想和方法）.精品学习资料可选择pdf第34页，共35页-----------------------\n请你用上面的思想和方法对下面关于圆的问题进行研究：(1)如图1，在圆O所在平面上，放置一条直线m（m和圆O分别交于点A、B），根据这个．．图形可以提出的概念或问题有哪些（直接写出两个即可）？(2)如图2，在圆O所在平面上，请你放置与圆O都相交且不同时经过圆心的两条直线m和n．．．．．．．．．（m与圆O分别交于点A、B，n与圆O分别交于点C、D）.请你根据所构造的图形提出一个结论，并证明之.ABC(3)如图3，其中AB是圆O的直径，AC是弦，D是的中点，弦DE⊥AB于点F.请找出点C和点E重合的条件，并说明理由.BEDmCGABAOFOOCD第25题图1第25题图2第25题图32100】抛物线yaxbxc(a)0的顶点为M，与x轴的交点为A、B（点B在点A的右侧），△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b。若关于x的一元二次方程2(ma)x2bx(ma)0有两个相等的实数根。（1）判断△ABM的形状，并说明理由。（2）当顶点M的坐标为（－2，－1）时，求抛物线的解析式，并画出该抛物线的大致图形。（3）若平行于x轴的直线与抛物线交于C、D两点，以CD为直径的圆恰好与x轴相切，求该圆的圆心坐标。精品学习资料可选择pdf第35页，共35页-----------------------