圆的性质(初中数学中考题汇总35) 43页

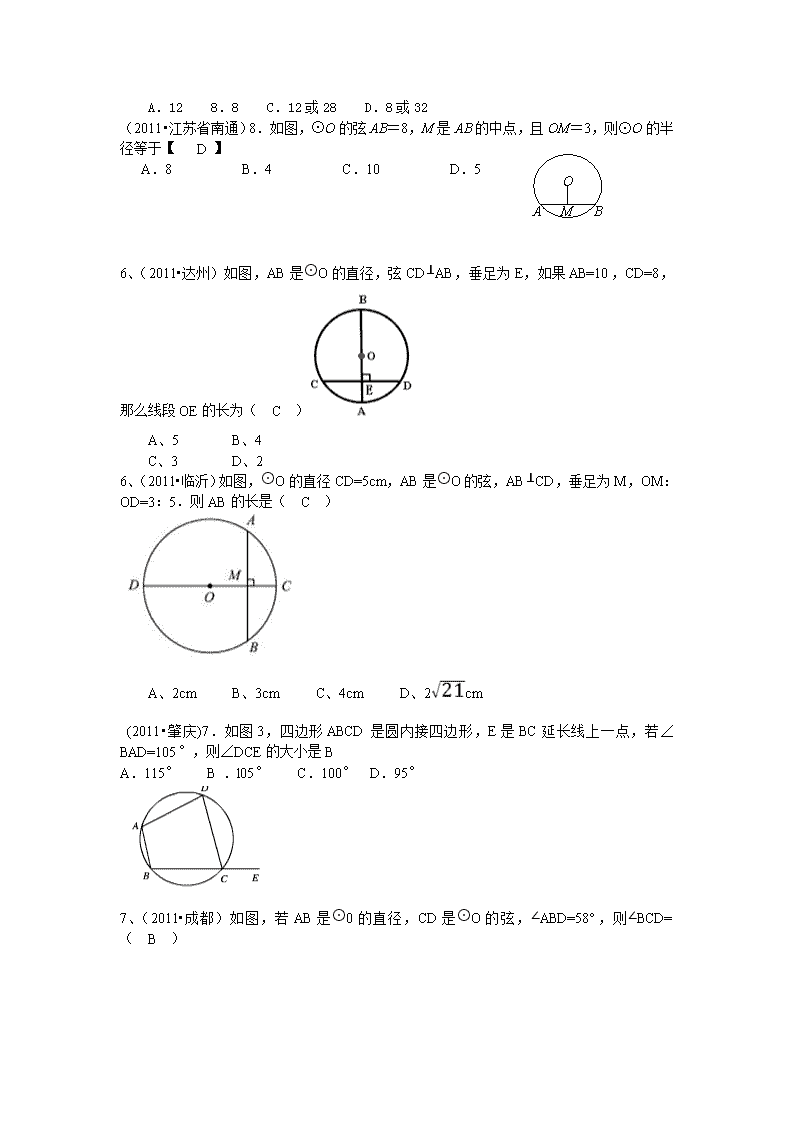
l选择题（每小题x分，共y分）（2011•福建省三明）7．如图，AB是⊙O的直径，C，D两点在⊙O上，若∠C＝40°，则∠ABD的度数为（B）A．40°B．50°C．80°D．90°（2011•四川省内江市）9、如图，⊙O是△ABC的外接圆，∠BAC=60°，若⊙O的半径0C为2，则弦BC的长为（　D　）A、1B、C、2D、12、（2011•毕节地区）如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为（　C　）A、2cmB、cmC、D、7、（2011•娄底）若⊙O的半径为5cm，点A到圆心O的距离为4cm，那么点A与⊙O的位置关系是（　C　）A、点A在圆外B、点A在圆上C、点A在圆内D、不能确定（2011•牡丹江）19．已知⊙0的直径AB=40，弦CD⊥AB于点E，且CD=32，则AE的长为(C)\nA．128．8C．12或28D．8或32ABOM（2011•江苏省南通）8．如图，⊙O的弦AB＝8，M是AB的中点，且OM＝3，则⊙O的半径等于【D】A．8B．4C．10D．56、（2011•达州）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10，CD=8，那么线段OE的长为（　C　）A、5B、4C、3D、26、（2011•临沂）如图，⊙O的直径CD=5cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OD=3：5．则AB的长是（　C　）A、2cmB、3cmC、4cmD、2cm(2011•肇庆)7．如图3，四边形ABCD是圆内接四边形，E是BC延长线上一点，若∠BAD=105°，则∠DCE的大小是BA．115°B．l05°C．100°D．95°7、（2011•成都）如图，若AB是⊙0的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD=（　B　）\nA、116°B、32°C、58°D、64°（2011•上海市）6．矩形ABCD中，AB＝8，，点P在边AB上，且BP＝3AP，如果圆P是以点P为圆心，PD为半径的圆，那么下列判断正确的是（C）．(A)点B、C均在圆P外；(B)点B在圆P外、点C在圆P内；(C)点B在圆P内、点C在圆P外；(D)点B、C均在圆P内．（2011•甘肃兰州）12.如图，⊙O过点B、C，圆心O在等腰Rt△ABC的内部，∠BAC=90°，OA=1，BC=6.则⊙O的半径为CA.6B.13C.D.（2011•重庆市）6．如图，⊙O是△ABC的外接圆，∠＝400，则∠A的度数等于（B）A．60°B．50°C．45°D．40°（2011•佛山）4、若的一条弧所对的圆周角为，则这条弧所对的圆心角是（C）A、B、C、D、以上答案都不对（2011•鸡西市）8．如图，A、B、C、D是⊙O上的四个点，AB=AC，AD交BC于点E，AE=3，ED=4，则AB的长为（C）A3B2CD3\n（2011•南充市）9.在圆柱形油槽内装有一些油。截面如图，油面宽AB为6分米，如果再注入一些油后，油面AB上升1分米，油面宽变为8分米，圆柱形油槽直径MN为（C）（A）6分米（B）8分米（C）10分米（D）12分米（2011•安徽省）7.如图，⊙半径是1，A、B、C是圆周上的三点，∠BAC=36°，则劣弧的长是………………………………………………………………………【B】第7题图A.B.C.D.（2011•达州）6、如图3,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段OE的长为CA、5　　B、4　　　C、3　D、2　（2011•重庆市潼南县）3.如图，AB为⊙O的直径，点C在⊙O上,∠A=30°,则∠B的度数为DA．15°B.30°C.45°D.60°〔2011•芜湖市〕8．如图，直径为10的⊙A山经过点C(0，5)和点0(0，0)，B是y轴右侧⊙A优弧上一点，则∠OBC的余弦值为(C)\nA.B．C.D．(2011●嘉兴)6．如图，半径为10的⊙O中，弦AB的长为16，则这条弦的弦心距为（　A　）（第6题）（A）6（B）8（C）10（D）12（2011•乐山）6．如图（3），CD是⊙O的弦，直径AB过CD的中点M，若∠BOC=40°，则∠ABD=C(A)40°(B)60°（C）70°（D）80°（2011•泰安市）10.如图，⊙O的弦AB垂直平分半径OC，若AB=则⊙O的半径为A（A）（B）（C）（D）〔2011•浙江省衢州〕10、如图，一张半径为1的圆形纸片在边长为a()的正方形内任意移动，则该正方形内，这张圆形纸片“不能接触到的部分”的面积是(D)(第10题)A、B、C、D、O1ACB1xy第10题图（2011•金华市）10.如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能\n够与该圆弧相切的是（C▲)A.点（0，3）　B.点（2，3）　C.点（5，1）D.点（6，1）第10题图（2011•茂名市）10、如图，正方形ABCD内接于⊙O，⊙O的直径为分米，若在这个圆面上随意抛一粒豆子，则豆子落在正方形ABCD内的概率是AA．B．C．D．ABCDO(第8题)〔2011•浙江省衢州〕8、一个圆形人工湖如图所示，弦AB是湖上的一座桥，已知桥AB长100m，测得圆周角∠ACB=45°，则这个人工湖的直径AD为(B)A、B、C、D、〔2011•德州市〕7．一个平面封闭图形内（含边界）任意两点距离的最大值称为该图形的“直径”，封闭图形的周长与直径之比称为图形的“周率”，下面四个平面图形（依次为正三角形、正方形、正六边形、圆）的周率从左到右依次记为，，，，则下列关系中正确的是B（A）>>（B）>>（C）>>（D）>>ABCDEFO（第6题）〔2011•福州市〕7．如图，顺次连结圆内接矩形各边的中点，得到菱形ABCD，若BD＝6，DF＝4，则菱形ABCD的边长为（D）A.4B.3C.5D.7〔2011•山东省烟台市〕11、如图，△ABC内接于⊙O，D为线段AB的中点，延长OD交⊙O于点E，连接AE，BE，则下列五个结论①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤,正确结论的个数是B\nA、2B、3C、4D、5l二、填空题（每小题x分，共y分）16、（2011•江津区）已知如图，在圆内接四边形ABCD中，∠B=30°，则∠D=　150°　．（2011•上海市）17．如图3，AB、AC都是圆O的弦，OM⊥AB，ON⊥AC，垂足分别为M、N，如果MN＝3，那么BC＝___6______．（2011•连云港）15．如图，点D为AC上一点，点O为边AB上一点，AD＝DO．以O为圆心，OD长为半径作圆，交AC于另一点E，交AB于点F，G，连接EF．若∠BAC＝22°，则∠EFG＝_▲．【答案】33°。（2011•无锡市）18．如图，以原点O为圆心的圆交X轴于A、B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB=20°，则∠OCD=65°．\nA第8题图CB（2011•黑龙江省龙东地区）8、如图，已知⊙O的半径为4，OC垂直弦AB于点C，∠AOB=120°，则弦AB长为4。（2011•湖北省咸宁）12．如图，梯形ABCD内接于⊙O，AD∥BC，，则的度数为98．ABCDO（第12题）8、（2011•黑河）如图，A、B、C、D是⊙O上的四个点，AB=AC，AD交BC于点E，AE=3，ED=4，则AB的长为．（2011•绥化市）8．如图，A、B、C、D处⊙O上的四个点．AB=AC．AD交BC于点E．AE=3，ED=4．则AB的长为___________．15、（2011•常州）如图，DE是⊙O的直径，弦AB⊥CD，垂足为C，若AB=6，CE=1，则OC=　4　，CD=　9　．（2011•长春）11．如图，将三角板的直角顶点放在⊙O的圆心上，两条直角边分别交⊙O于A、B两点，点P在优弧AB上，且与点A、B不重合，连结PA、PB.则∠APB的大小为_45__度．\n（第11题）（2011•深圳市）14、如图5，在⊙O中，圆心角∠AOB=120º，弦AB=cm，则OA=4cm.（2011•广西玉林）18、如图，AB是半圆O的直径，以0A为直径的半圆O′与弦AC交于点D，O′E∥AC，并交OC于点E．则下列四个结论：18题图①点D为AC的中点；②；③；④四边形O'DEO是菱形．其中正确的结论是____①③④______．（把所有正确的结论的序号都填上）（2011•龙岩市）16．如图．⊙O是△ABC的外接圆AC是⊙O的直径，OD⊥BC于点D．OD=2．则AB的长是____4_____19．（2011·西宁）如图10，在⊙O中，AB、AC是互相垂直的两条弦，OD⊥AB于点D，OE⊥AC于点E，且AB＝8cm，AC＝6cm，那么⊙O的半径OA长为_▲．\nOBACED【答案】5cm（2011•扬州市）15．如图，的弦与直线径相交，若，则=____40_______°.OBDAC（第15题）12．（2011·辽阜新）如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于点E，若AB＝2DE，∠B＝18°，则∠AOC的度数为_▲．OABDCE【答案】54第13题图（2011•安徽省）13.如图，⊙O的两条弦AB、CD互相垂直，垂足为E，且AB=CD，已知CE=1，ED=3，则⊙O的半径是_________.16．（2011·湖南衡阳），16，3分）如图，⊙的直径过弦的中点G，∠EOD=40°，则∠FCD的度数为．\n【答案】20（2011•天津）(1S)如图，AD，AC分别是⊙O的直径和弦．且∠CAD=30°．OB⊥AD，交AC于点B．若OB=5，则BC的长等于_____5____。16、（2011•娄底）如图，△ABC内接于⊙O，已知∠A=55°，则∠BOC=　110°　．（2011•甘肃兰州）16.如图，OB是⊙O的半径，点C、D在⊙O上，∠DCB=27°，则∠OBD=63度.13、（2011•綦江县）如图，已知AB为⊙O的直径，∠CAB=30°，则∠D=　60°　．（2011•郴州）10.如图3，四边形ABCD是O的内接四边形，∠DCE＝，则图3\n∠BAD＝____60__________.(2011•威海市)15．如图，⊙O的直径AB与弦CD交于点E，AE=5，BE=1，CD=4，则∠AED=____30____。ABODEC•（第15题图）〔2011•温州市〕14、如图，AB是⊙O的直径，点C,D都在⊙O上，连结CA,CB,DC,DB.已知∠D=30°，BC=3，则AB的长是6；（第16题）(2011●嘉兴)16．如图，AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB交弧BC于点D，连结CD、OD，给出以下四个结论：①AC∥OD；②；③△ODE∽△ADO；④．其中正确结论的序号是　①④▲　．（2011•黄石市）14.如图（5），△内接于⊙，若＝30°，，则⊙的直径为.BCAO图（5）\n16、（2011•湛江）如图，A，B，C是⊙O上的三点，∠BAC=30°，则∠BOC=　60　度．(2011●河北省)16．如图7，点O为优弧ACB所在圆的心，∠AOC=108°，点D在AB的延长线上，BD=BC，则∠D=___27_________.ABCDO图72011•芜湖市〕16.如图，在正方形ABCD内有一折线段，其中AE⊥EF，EF⊥FC,并且AE=6，EF=8，FC=10，则正方形与其外接圆之间形成的阴影部分的面积为_____80π-160___。〔2011•日照市〕14．如图，在以AB为直径的半圆中，有一个边长为1的内接正方形CDEF，则以AC和BC的长为两根的一元二次方程是如：x2-x+1=0；．〔2011•南京市〕13．如图，海边有两座灯塔A、B，暗礁分布在经过A、B\n两点的弓形（弓形的弧是⊙O的一部分）区域内ABOP(第12题)，∠AOB=80°，为了避免触礁，轮船P与A、B的张角∠APB的最大值为__40____°．〔2011•福建省泉州市〕16.已知三角形的三边长分别为3，4，5，则它的边与半径为1的圆的公共点个数所有可能的情况是2.（写出符合的一种情况即可）l三、解答题：（共x分）（2011•张家界）24、（本题8分）如图，在⊙Ｏ中，直径ＡＢ的两侧有定点Ｃ和动点Ｐ，点Ｐ在弧ＡＢ上运动（不与A、B重合），过点C作ＣＰ的垂线，与ＰＢ的延长线交于点Ｑ.（１）试猜想：△ＰＣＱ与△ＡＣＢ具有何种关系？（不要求证明）；（２）当点Ｐ运动到什么位置时，△ABC≌△PCB,并给出证明.24、（1）△PCQ～△ACB…………………………3分（2）当PC过圆心时，△ABC△PCB…..4分证明：∵PC和AB都是⊙O的直径∴∠ACB=∠PBC=90°……………………5分且AB=PC………………………………6分又∠A=∠P…………………………….7分∴△ABC≌△PCB……………………..8分\n25.（2011山东烟台，25，12分）已知：AB是⊙O的直径，弦CD⊥AB于点G，E是直线AB上一动点（不与点A、B、G重合），直线DE交⊙O于点F，直线CF交直线AB于点P.设⊙O的半径为r.（1）如图1，当点E在直径AB上时，试证明：OE·OP＝r2（2）当点E在AB（或BA）的延长线上时，以如图2点E的位置为例，请你画出符合题意的图形，标注上字母，（1）中的结论是否成立？请说明理由.ABCDEFP.OG（图1）.ABCDE.OG（图2）【解】（1）证明：连接FO并延长交⊙O于Q，连接DQ.∵FQ是⊙O直径，∴∠FDQ＝90°.∴∠QFD＋∠Q＝90°.∵CD⊥AB，∴∠P＋∠C＝90°.∵∠Q＝∠C，∴∠QFD＝∠P.∵∠FOE＝∠POF，∴△FOE∽△POF.∴.∴OE·OP＝OF2＝r2.（2）解：（1）中的结论成立.理由：如图2，依题意画出图形，连接FO并延长交⊙O于M，连接CM.∵FM是⊙O直径，∴∠FCM＝90°，∴∠M＋∠CFM＝90°.∵CD⊥AB，∴∠E＋∠D＝90°.∵∠M＝∠D，∴∠CFM＝∠E.∵∠POF＝∠FOE，∴△POF∽△FOE.∴，∴OE·OP＝OF2＝r2.【思路分析】（1）要证等积式，需要将其化为比例式，再利用相似证明.观察图形，此题显然要连半径OF，构造OE、OP所在的三角形，这样问题便转化为证明△FOE∽△POF了.而要证明△FOE∽△POF，由于已经存在一个公共角，因此只需再证明另一角对应相等即可，这一点利用圆周角定理及其推论可获证，且方法不惟一；（2）同（1）类似.【方法规律】此题综合考查圆的性质及相似的知识，解题关键是辅助线的灵活添加.\n值得注意的是（2）问是（1）知识的变式，能开拓视野，提高思维深度、灵敏性，其证明同（1）类似，可不必证明.22．（2011湖北鄂州，22，8分）在圆内接四边形ABCD中，CD为∠BCA外角的平分线，F为弧AD上一点，BC=AF，延长DF与BA的延长线交于E．⑴求证△ABD为等腰三角形．⑵求证AC•AF=DF•FE 第22题图BAFEDCM【解题思路】（1）利用同角的补角相等，同弧所对的圆周角相等，等量代换；（2）证等积式就要找三角形相似，发现AC、AF、FE所在的三角形，且利用等弧对等弦，同圆中等弦对等弧，发现DF可以被DC替换，进而求解。【答案】⑴由圆的性质知∠MCD=∠DAB、∠DCA=∠DBA，而∠MCD=∠DCA，所以∠DBA=∠DAB，故△ABD为等腰三角形．⑵∵∠DBA=∠DAB∴弧AD=弧BD又∵BC=AF∴弧BC=弧AF、∠CDB=∠FDA∴弧CD=弧DF∴CD=DF再由“圆的内接四边形外角等于它的内对角”知∠AFE=∠DBA=∠DCA①，∠FAE=∠BDE∴∠CDA=∠CDB＋∠BDA=∠FDA＋∠BDA=∠BDE=∠FAE②由①②得△DCA∽△FAE∴AC：FE=CD：AF∴AC•AF=CD•FE而CD=DF，∴AC•AF=DF•FE（2011•泰州市）26．（本题满分10分）如图，以点O为圆心的两个同心圆中，矩形ABCD的边BC为大圆的弦，边AD与小圆相切于点M，OM的延长线与BC相交于点N。（1）点N是线段BC的中点吗？为什么？（2）若圆环的宽度（两圆半径之差）为6cm，AB=5cm，BC=10cm，求小圆的半径。21世纪教育网【答案】解：（1）点N是线段BC的中点，理由如下：∵AD与小圆相切于点M∴ON⊥AD又∵AD∥BC∴ON⊥BC∴点N是线段BC的中点\n（2）连接OB,设小圆的半径为r，则ON=r+5,OB=r+6,且BN=5在Rt△OBN中：5²+(r+5)²=(r+6)²解得：r=7cm答：小圆的半径7cm。ABECD（2011•潜江市）20．（满分8分）如图，BD是⊙O的直径，A、C是⊙O上的两点，且AB=AC，AD与BC的延长线交于点E.（1）求证：△ABD∽△AEB；（2）若AD=1，DE=3，求BD的长.20.（1）证明：∵AB=AC，∴.∴∠ABC=∠ADB.……………………2分又∠BAE=∠DAB，∴△ABD∽△AEB.…………………………………4分（2）解：∵△ABD∽△AEB，∴.∵AD=1，DE=3，∴AE=4.∴AB2=AD·AE=1×4=4.∴AB=2.……………………………………………………………………6分∵BD是⊙O的直径，∴∠DAB=90°.在Rt△ABD中，BD2=AB2＋AD2=22＋12=5，∴BD=.…………………………………………………………………8分21、（2011•金华）如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连接OA，此时有OA∥PE．（1）求证：AP=AO；（2）若tan∠OPB=，求弦AB的长；（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为　P、A、O、C　，能构成等腰梯形的四个点为　A、B、D、C　或　P、A、O、D　或　P、C、O、B　．考点：垂径定理；勾股定理；菱形的判定；等腰梯形的判定；锐角三角函数的定义。专题：证明题。分析：\n（1）由已知条件“射线PG平分∠EPF”求得∠DPO=∠BPO；然后根据平行线的性质，两直线OA∥PE，内错角∠DPO=∠POA；最后由等量代换知∠BPO=∠POA，从而根据等角对等边证明AP=AO；（2）设OH=x，则PH=2x．作辅助线OH（“过点O作OH⊥AB于点H”），根据垂径定理知AH=HB=AB；又有已知条件“tan∠OPB=”求得PH=2OH；然后利用（1）的结果及勾股定理列出关于x的一元二次方程，解方程即可；（3）根据菱形的性质、等腰梯形的判定定理填空．解答：（1）∵PG平分∠EPF，∴∠DPO=∠BPO，∵OA∥PE，∴∠DPO=∠POA，∴∠BPO=∠POA，∴PA=OA；（2分）（2）过点O作OH⊥AB于点H，则AH=HB=AB，（1分）∵tan∠OPB=，∴PH=2OH，（1分）设OH=x，则PH=2x，由（1）可知PA=OA=10，∴AH=PH﹣PA=2x﹣10，∵AH2+OH2=OA2，∴（2x﹣10）2+x2=102，（1分）解得x1=0（不合题意，舍去），x2=8，∴AH=6，∴AB=2AH=12；（1分）（3）P、A、O、C；A、B、D、C或P、A、O、D或P、C、O、B．（2分）（写对1个、2个、3个得（1分），写对4个得2分）点评：本题综合考查了垂径定理、勾股定理、菱形的性质、等腰梯形的判定定理及锐角三角函数的定义．解此类题目要注意将圆的问题转化成三角形的问题再进行计算． 第22题图BAFEDCM（2011•随州）22．（10分）在圆内接四边形ABCD中，CD为∠BCA外角的平分线，F为上一点，BC＝AF，延长DF与BA的延长线交于E．（1）求证△ABD为等腰三角形．（2）求证AC•AF＝DF•FE．22．（1）证法一：连CF、BF\n∠ACD=∠MCD=∠CDB＋∠CBD=∠CFB＋∠CFD=∠DFB而∠ACD=∠DFB=∠DAB又∠ACD=∠DBA∴∠DAB=∠DBA∴△ABD为等腰三角形……（4分）证法二：由题意有∠MCD=∠ACD=∠DBA,又∠MCD+∠BCD=∠DAB+∠BCD=180°,∴∠MCD=∠DAB，∴∠DAB=∠DBA即△.ABD为等腰三角形……（4分）（2）由（1）知AD=BD，BC=AF，则弧AFD=弧BCD，弧AF=弧BC，∴弧CD=弧DF,∴弧CD=弧DF……①……（5分）又BC=AF,∴∠BDC=∠ADF,∠BDC＋∠BDA=∠ADF＋∠BDA，即∠CDA=∠BDF，而∠FAE＋∠BAF=∠BDF＋∠BAF=180°，∴∠FAE=∠BDF=∠CDA，同理∠DCA=∠AFE……（8分）∴在△CDA与△FDE中，∠CDA=∠FAE，∠DCA=∠AFE∴△CDA∽△FAE∴,即CD·EF=AC·AF，又由①有AC·AF=DF·EF命题即证……（10分）（2011•湖北省宜昌市）21．如图，D是△ABC的边BC的中点,过AD延长线上的点E作AD的垂线EF，E为垂足，EF与AB的延长线相交于点F，点O在AD上，AO＝CO，BC∥EF．(1)证明：AB＝AC；(2)证明：点O是△ABC的外接圆的圆心；(3)当AB＝5，BC＝6时，连接BE，若∠ABE＝90°，求AE的长．(1)∵AE⊥EF， EF∥BC，∴AD⊥BC．(1分)在△ABD和△ACD中，∵BD＝CD，∠ADB＝∠ADC，AD＝AD，∴△ABD≌△ACD．(或者：又∵BD＝CD，∴AE是BC的中垂线．) (2分)∴AB＝AC． (3分)(2)连BO，∵AD是BC的中垂线，∴BO＝CO．(或者：证全等也可得到BO＝CO．)\n又AO＝CO，∴AO＝BO＝CO．(4分)∴点O是△ABC外接圆的圆心． (5分)（3）解法1：∵∠ABE＝∠ADB=90°，∴∠ABD+∠BAD=∠AEB+∠BAE=90°，∴∠ABD=∠AEB． 又∵∠BAD=∠EAB，∴△ABD∽△AEB．∴(或者：由三角函数得到) （6分）在Rt△ABD中，∵AB=5，BD=BC=3，∴AD=4．（7分）∴AE=．(8分)解法2：∵AO＝BO， ∴∠ABO＝∠BAO．∵∠ABE＝90°，∴∠ABO＋∠OBE＝∠BAO＋∠AEB＝90°．∴∠OBE＝∠OEB，∴OB＝OE．(6分)在 Rt△ABD中，∵AB=5，BD=BC=3，∴AD=4． 设 OB＝x， 则 OD＝4－x，由32+（4-x)2=x2,解得x=．(7分)∴AE＝2OB＝．(8分)解法3：设AO的延长线与⊙O交于点E1，则AE1是⊙O的直径， ∴∠ABE1=90°．在Rt△ABE和Rt△ABE1中，∵∠BAE＝∠BAE1，∠ABE＝∠ABE1＝90°，AB＝AB,∴△ABE≌△ABE1，∴AE=AE1． (6分)(同方法2)∵BO=．（7分）∴AE=2OB=．(8分)小明：那直角三角形中是否存在奇异三角形呢？（2011•宁波）25．（本题10分）阅读下面的情景对话，然后解答问题：老师：我们新定义一种三角形，两边平方和等于第三边平方的2倍的三角形叫做奇异三角形．\n小华：等边三角形一定是奇异三角形！（1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命题还是假命题？（2）在Rt△ABC中，∠ACB＝90°，AB=，AC=，BC=，且，若Rt△ABC是奇异三角形，求；(第25题)ABCDEO（3）如图，AB是⊙O的直径，C是⊙O上一点(不与点A、B重合)，D是半圆ADB的中点，C、D在直径AB两侧，若在⊙O内存在点E，使得AE=AD，CB=CE．①求证：△ACE是奇异三角形；②当△ACE是直角三角形时，求∠AOC的度数．25．解：(1)真命题2分(2)在Rt△ABC中，∵∴，∴若Rt△ABC为奇异三角形,一定有3分∴∴得∵∴∴5分(3)①∵AB是⊙O的直径∴∠ACB=∠ADB=90°在Rt△ACB中，在Rt△ADB中，∵点D是半圆ADB的中点∴AD=BD∴AD=BD6分\n∴∴7分又∵∴∴△是奇异三角形8分②由①可得△是奇异三角形∴当△是直角三角形时由（2）可得或　（Ⅰ）当时，即∵∴∴9分（Ⅱ）当时，即∵∴∴∴的度数为．10分　（2011•宿迁市）26．（本题满分10分）如图，在平面直角坐标系中，O为坐标原点，P是反比例函数y＝（x＞0）图象上的任意一点，以P为圆心，PO为半径的圆与x、y轴分别交于点A、B．（1）判断P是否在线段AB上，并说明理由；（2）求△AOB的面积；（3）Q是反比例函数y＝（x＞0）图象上异于点P的另一点，请以Q为圆心，QO半径画圆与x、y轴分别交于点M、N，连接AN、MB．求证：AN∥MB．解：（1）点P在线段AB上，理由如下：（第26题）∵点O在⊙P上，且∠AOB＝90°∴AB是⊙P的直径∴点P在线段AB上．（2）过点P作PP1⊥x轴，PP2⊥y轴，由题意可知PP1、PP2是△AOB的中位线，故S△AOB＝OA×OB＝×2PP1×PP2∵P是反比例函数y＝（x＞0）图象上的任意一点∴S△AOB＝OA×OB＝×2PP1×2PP2＝2PP1×PP2＝12．\n（3）如图，连接MN，则MN过点Q，且S△MON＝S△AOB＝12．∴OA·OB＝OM·ON∴∵∠AON＝∠MOB∴△AON∽△MOB∴∠OAN＝∠OMB∴AN∥MB．（2011•遵义）27．（14分）已知抛物线经过A(3，0),B(4，1)两点，且与y轴交于点C。（1）求抛物线的函数关系式及点C的坐标；（2）如图（1）,连接AB，在题（1）中的抛物线上是否存在点P，使△PAB是以AB为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；（3）如图（2）,连接AC，E为线段AC上任意一点（不与A、C重合）经过A、E、O三点的圆交直线AB于点F，当△OEF的面积取得最小值时，求点E的坐标。27．解：（1）（3分）将A(3,0),B(4,1)代人得∴∴∴C(0,3)(2)(7分)假设存在，分两种情况，如图.①连接AC,∵OA=OC=3,∴∠OAC=∠OCA=45O.……1分过B作BD⊥轴于D，则有BD=1，,∴BD=AD,∴∠DAB=∠DBA=45O.∴∠BAC=180O-45O-45O=90O……………2分\n∴△ABC是直角三角形.∴C(0,3)符合条件.∴P1(0,3)为所求.②当∠ABP=90O时,过B作BP∥AC,BP交抛物线于点P.∵A(3,0),C(0,3)∴直线AC的函数关系式为将直线AC向上平移2个单位与直线BP重合.则直线BP的函数关系式为由,得又B(4,1),∴P2(-1,6).综上所述,存在两点P1(0,3),P2(-1,6).另解②当∠ABP=90O时,过B作BP∥AC,BP交抛物线于点P.∵A(3,0),C(0,3)∴直线AC的函数关系式为将直线AC向上平移2个单位与直线BP重合.则直线BP的函数关系式为∵点P在直线上，又在上.∴设点P为∴解得∴P1(-1,6),P2(4,1)(舍)综上所述,存在两点P1(0,3),P2(-1,6).(3)(4分)∵∠OAE=∠OAF=45O,而∠OEF=∠OAF=45O,∠OFE=∠OAE=45O,∴∠OEF=∠OFE=45O,∴OE=OF,∠EOF=90O∵点E在线段AC上,∴设E∴=∴==\n=∴当时,取最小值,此时,∴26、（2011•苏州）如图，已知AB是⊙O的弦，OB=2，∠B=30°，C是弦AB上的任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD．（1）弦长等于　2（结果保留根号）；（2）当∠D=20°时，求∠BOD的度数；（3）当AC的长度为多少时，以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似？请写出解答过程．考点：圆周角定理；垂径定理；相似三角形的判定与性质；解直角三角形。专题：几何综合题；数形结合。分析：（1）过点O作OE⊥AB于E，由垂径定理即可求得AB的长；（2）连接OA，由OA=OB，OA=OD，可得∠BAO=∠B，∠DAO=∠D，则可求得∠DAB的度数，又由圆周角等于同弧所对圆心角的一半，即可求得∠DOB的度数；（3）由∠BCO=∠A+∠D，可得要使△DAC与△BOC相似，只能∠DCA=∠BCO=90°，然后由相似三角形的性质即可求得答案．\n解答：解：过点O作OE⊥AB于E，则AE=BE=AB，∠OEB=90°，∵OB=2，∠B=30°，∴BE=OB•cos∠B=2×=，∴AB=2；故答案为：2；（2）连接OA，∵OA=OB，OA=OD，∴∠BAO=∠B，∠DAO=∠D，∴∠DAB=∠BAO+∠DAO=∠B+∠D，又∵∠B=30°，∠D=20°，∴∠DAB=50°，∴∠BOD=2∠DAB=100°；（3）∵∠BCO=∠A+∠D，∴∠BCO＞∠A，∠BCO＞∠D，∴要使△DAC与△BOC相似，只能∠DCA=∠BCO=90°，此时∠BOC=60°，∠BOD=120°，∴∠DAC=60°，∴△DAC∽△BOC，∵∠BCO=90°，即OC⊥AB，\n∴AC=AB=．点评：此题考查了垂径定理，圆周角的性质以及相似三角形的判定与性质等知识．题目综合性较强，解题时要注意数形结合思想的应用．（2011•宜宾）已知：在△ABC中，以AC边为直径的⊙O交BC于点D，在劣弧上取一点E使∠EBC=∠DEC，延长BE依次交AC于G，交⊙O于H.(1)求证：AC⊥BH(23题图)(2)若∠ABC=45°，⊙O的直径等于10，BD=8，求CE的长.23．证明：（1）连结AD(1分)∵∠DAC=∠DEC∠EBC=∠DEC∴∠DAC=∠EBC(2分)又∵AC是⊙O的直径∴∠ADC=90°(3分)∴∠DCA+∠DAC=90°∴∠EBC+∠DCA=90°∴∠BGC=180°–（∠EBC+∠DCA)=180°–90°=90°∴AC⊥BH（5分）（2）∵∠BDA=180°–∠ADC=90°∠ABC=45°∴∠BAD=45°(23题图)∴BD=AD∵BD=8∴AD=8（6分）又∵∠ADC=90°AC=10∴由勾股定理DC===6∴BC=BD+DC=8+6=14(7分)又∵∠BGC=∠ADC=90°∠BCG=∠ACD∴△BCG∽△ACD∴=∴=∴CG=(8分)连结AE∵AC是直径∴∠AEC=90°又因EG⊥AC∴△CEG∽△CAE∴=∴CE2=AC·CG=´10=84∴CE==2（10分）（2011•长沙市）22．如图，在⊙O中，直径AB与弦CD相交于点P，∠CAB=40°，∠APD=65°。\n（1）求∠B的大小：（2）已知圆心0到BD的距离为3，求AD的长。22.（1）证明略（2）AD=2OE=6（2011•金华市）在平面直角坐标系中，如图1，将个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在轴和轴的正半轴上,设抛物线（＜0）过矩形顶点B、C.（1）当n=1时，如果=-1，试求b的值；（2）当n=2时，如图2，在矩形OABC上方作一边长为1的正方形EFMN，使EF在线段CB上，如果M，N两点也在抛物线上，求出此时抛物线的解析式；图1图2图3xyMNxOCEABFAByCO…xOyACB（3）将矩形OABC绕点O顺时针旋转，使得点B落到轴的正半轴上，如果该抛物线同时经过原点O.①试求当n=3时a的值；②直接写出关于的关系式．27、（2011•苏州）已知四边形ABCD是边长为4的正方形，以AB为直径在正方形内作半圆，P是半圆上的动点（不与点A、B重合），连接PA、PB、PC、PD．（1）如图①，当PA的长度等于　2时，∠PAD=60°；当PA的长度等于　2或时，△PAD是等腰三角形；（2）如图②，以AB边所在直线为x轴、AD边所在直线为y轴，建立如图所示的直角坐标系（点A即为原点O），把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3．设P点坐标为（a，b），试求2S1S3﹣S22的最大值，并求出此时a、b的值．考点\n：相似三角形的判定与性质；二次函数的最值；正方形的性质；圆周角定理；解直角三角形。专题：几何综合题；数形结合；方程思想。分析：（1）由AB是直径，可得∠APB=90°，然后利用三角函数即可求得PA的长；当PA=PB时，△PAB是等腰三角形，然后由等腰三角形的性质与射影定理即可求得答案．（2）过点P分别作PE⊥AB，PF⊥AD，垂足分别为E，F延长FP交BC于点G，则PG⊥BC，P点坐标为（a，b），PE=b，PF=a，PG=4﹣a，利用矩形的面积关系与二次函数的知识即可求得答案．解答：解：（1）若∠PAD=60°，需∠PAB=30°，∵AB是直径，∴∠APB=90°，∴PB=2，则PA=2，∴当PA的长度等于2时，∠PAD=60°；若△PAD是等腰三角形，则只能是PA=PD，过点P作PE⊥AD于E，作PM⊥AB于M，则四边形EAMP是矩形，∴PM=PE=AB=2，∵PM2=AM•BM=4，∵AM+BM=4，∴AM=2，∴PA=2，同理可得P在P′时，PA=PB，此时：PA=；∴当PA的长度等于2或时，△PAD是等腰三角形；\n（2）过点P分别作PE⊥AB，PF⊥AD，垂足分别为E，F延长FP交BC于点G，则PG⊥BC，∵P点坐标为（a，b），∴PE=b，PF=a，PG=4﹣a，在△PAD，△PAB及△PBC中，S1=2a，S2=2b，S3=8﹣2a，∵AB为直径，∴∠APB=90°，∴PE2=AE•BE，即b2=a（4﹣a），∴2S1S3﹣S22=4a（8﹣2a）﹣4b2=﹣4b2+16a=﹣4（a﹣2）2+16，∴当a=2时，b=2，2S1S3﹣S22有最大值16．点评：此题考查了正方形的性质，圆周角的性质以及三角函数的性质等知识．此题综合性很强，解题时要注意数形结合与方程思想的应用．（2011•邵阳市）24．如图（十一）所示，在平面直角坐标系Oxy中，已知点A(－，0)，点C(0，3)，点B是x轴上一点(位于点A的右侧)，以AB为直径的圆恰好经过点C．（1）求∠ACB的度数；（2）已知抛物线y＝ax2＋bx＋3经过A、B两点，求抛物线的解析式；（3）线段BC上是否存在点D，使△BOD为等腰三角形．若存在，则求出所有符合条件的点D的坐标；若不存在，请说明理由．解：(1)∵以AB为直径的圆恰好经过点C∴∠ACB=(2)∵△AOC∽△ABC∴∵A(－，0)，点C(0，3)，∴∴∴∴B(4,0)把A、B、C三点坐标代入得(3)1）OD=OB,D在OB的中垂线上，过D作DH⊥OB,垂足是H则H是OB中点。\nDH=∴D2)BD=BO过D作DG⊥OB,垂足是G∴OG:OB=CD:CBDG:OC=1:5∴OG:4=1:5DG:3=1:5∴OG=DG=∴D(,)图1124.(本题12分)第24题图OBDECFxyA（2011•金华市）如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连结OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连结CF．（1）当∠AOB=30°时，求弧AB的长度；（2）当DE=8时，求线段EF的长；（3）在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似，若存在，请求出此[来源:学科网ZXXK]时点E的坐标；若不存在，请说明理由．23.(本题10分)（1）由题意可知，抛物线对称轴为直线x=，∴,得xyOCEABMNFb=1；……2分yxOCAB（2）设所求抛物线解析式为，由对称性可知抛物线经过点B（2，1）和点M（，2）∴解得∴所求抛物线解析式为；……4分（3）①当n=3时，OC=1，BC=3，设所求抛物线解析式为，xyOABCD过C作CD⊥OB于点D，则Rt△OCD∽Rt△CBD，∴,设OD=t，则CD=3t，∵，∴，∴,∴C（，）,又B（，0），∴把B、C坐标代入抛物线解析式，得\n解得:a=；……2分②.……2分24.(本题12分)（1）连结BC,∵A（10，0）,∴OA=10,CA=5,∵∠AOB=30°,∴∠ACB=2∠AOB=60°,OBDECFxyA∴弧AB的长=;……4分（2）连结OD,∵OA是⊙C直径,∴∠OBA=90°,又∵AB=BD,∴OB是AD的垂直平分线,∴OD=OA=10,在Rt△ODE中，OE=,∴AE=AO－OE=10-6=4,由∠AOB=∠ADE=90°-∠OAB，∠OEF=∠DEA，得△OEF∽△DEA,∴,即，∴EF=3；……4分OBDFCEAxy（3）设OE=x，①当交点E在O，C之间时，由以点E、C、F为顶点的三角形与△AOB相似，有∠ECF=∠BOA或∠ECF=∠OAB，当∠ECF=∠BOA时，此时△OCF为等腰三角形，点E为OC中点，即OE=，∴E1（，0）；当∠ECF=∠OAB时，有CE=5-x,AE=10-x，∴CF∥AB,有CF=,∵△ECF∽△EAD,OBDFCEAxy∴,即,解得：,∴E2（，0）;②当交点E在点C的右侧时，∵∠ECF＞∠BOA，∴要使△ECF与△BAO相似，只能使∠ECF=∠BAO，\nOBDFCEAxy连结BE，∵BE为Rt△ADE斜边上的中线，∴BE=AB=BD,∴∠BEA=∠BAO,∴∠BEA=∠ECF,∴CF∥BE,∴,∵∠ECF=∠BAO,∠FEC=∠DEA=Rt∠，∴△CEF∽△AED,∴,而AD=2BE,∴,即,解得,＜0（舍去），∴E3（，0）;③当交点E在点O的左侧时，∵∠BOA=∠EOF＞∠ECF.∴要使△ECF与△BAO相似，只能使∠ECF=∠BAOOBDFCEAxy连结BE，得BE==AB，∠BEA=∠BAO∴∠ECF=∠BEA,∴CF∥BE,∴,又∵∠ECF=∠BAO,∠FEC=∠DEA=Rt∠，∴△CEF∽△AED,∴，而AD=2BE,∴,∴,解得,＜0（舍去）,∵点E在x轴负半轴上,∴E4（，0）,综上所述：存在以点E、C、F为顶点的三角形与△AOB相似,此时点E坐标为：（，0）、（，0）、（，0）、（，0）．……4分（2011•江西省）21.如图，已知⊙O的半径为2，弦BC的长为，点A为弦BC所对优弧上任意一点（B，C两点除外）.\n（1）求∠BAC的度数；（2）求△ABC面积的最大值.ABCO（参考数据：，，.）21．解：(1)解法一ABCOE连接OB，OC，过O作OE⊥BC于点E.∵OE⊥BC，BC=，∴.………………1分在Rt△OBE中，OB=2，∵，∴,∴，∴.………………4分ABCOD解法二连接BO并延长，交⊙O于点D，连接CD.∵BD是直径，∴BD=4，.在Rt△DBC中，,∴，∴.………………4分(2)解法一因为△ABC的边BC的长不变，所以当BC边上的高最大时，△ABC的面积最大，此时点A落在优弧BC的中点处.………………5分过O作OE⊥BC于E，延长EO交⊙O于点A，则A为优弧BC的中点.连接AB，AC，则AB=AC，.ABCOE在Rt△ABE中，∵，∴，∴S△ABC=.答：△ABC面积的最大值是.………………8分解法二因为△ABC的边BC的长不变，所以当BC边上的高最大时，△ABC的面积最大，此时点A落在优弧BC的中点处.………………5分过O作OE⊥BC于E，延长EO交⊙O于点A，则A为优弧BC的中点.连接AB，AC，则AB=AC.∵,∴△ABC是等边三角形.………………6分在Rt△ABE中，∵，\n∴，∴S△ABC=.答：△ABC面积的最大值是.………………8分 第22题图BAFEDCM（2011•黄冈市）22．（8分）在圆内接四边形ABCD中，CD为∠BCA外角的平分线，F为弧AD上一点，BC=AF，延长DF与BA的延长线交于E．⑴求证△ABD为等腰三角形．⑵求证AC•AF=DF•FE22．⑴由圆的性质知∠MCD=∠DAB、∠DCA=∠DBA，而∠MCD=∠DCA，所以∠DBA=∠DAB，故△ABD为等腰三角形．⑵∵∠DBA=∠DAB∴弧AD=弧BD又∵BC=AF∴弧BC=弧AF、∠CDB=∠FDA∴弧CD=弧DF∴CD=DF再由“圆的内接四边形外角等于它的内对角”知∠AFE=∠DBA=∠DCA①，∠FAE=∠BDE∴∠CDA=∠CDB＋∠BDA=∠FDA＋∠BDA=∠BDE=∠FAE②由①②得△DCA∽△FAE∴AC：FE=CD：AF∴AC•AF=CD•FE\n而CD=DF，∴AC•AF=DF•FE\n（2011•金华市）如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连结OA，此时有OA//PE．（1）求证：AP=AO；（2）若tan∠OPB=，求弦AB的长；PABCODEFG第21题图（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为▲，能构成等腰梯形的四个点为▲或▲或▲.（1）∵PG平分∠EPF，∴∠DPO=∠BPO，∵OA//PE，∴∠DPO=∠POA，∴∠BPO=∠POA，HPABCODEFG∴PA=OA；……2分（2）过点O作OH⊥AB于点H，则AH=HB=AB，……1分[来源:学科网ZXXK]∵tan∠OPB=，∴PH=2OH，……1分设OH=，则PH=2，由（1）可知PA=OA=10，∴AH=PH－PA=2－10，∵，∴，……1分解得（不合题意，舍去），，∴AH=6，∴AB=2AH=12；……1分（3）P、A、O、C；A、B、D、C或P、A、O、D或P、C、O、B.……2分(写对1个、2个、3个得1分，写对4个得2分)〔2011•广州市〕25.（14分）如图7，⊙O中AB是直径，C是⊙O上一点，∠ABC=450，等腰直角三角形DCE中∠DCE是直角，点D在线段AC上。（1）证明：B、C、E三点共线；（2）若M是线段BE的中点，N是线段AD的中点，证明：MN=OM；（3）将△DCE绕点C逆时针旋转（00<<900）后，记为△D1CE1（图8），若M1是线段BE1的中点，N1是线段AD1的中点，M1N1=OM1是否成立？若是，请证明：若不是，说明理由。\n25、（1）证明：∵AB是⊙O的直径∴∠ACB=90°∵∠DCE=90°∴∠ACB＋∠DCE=180°∴B、C、E三点共线。(2)证明：连接ON、AE、BD，延长BD交AE于点F∵∠ABC=45°，∠ACB=90°∴BC=AC，又∠ACB=∠DCE=90°，DC=EC∴△BCD≌△ACE∴BD=AE，∠DBC=∠CAE∴∠DBC＋∠AEC=∠CAE＋∠AEC=90°∴BF⊥AE∵AO=OB，AN=ND∴ON=BD，ON∥BD∵AO=OB，EM=MB∴OM=AE，OM∥AE∴OM=ON，OM⊥ON∴∠OMN=45°，又cos∠OMN=∴\n(3)成立，证明同（2）。〔2011•德州市〕●观察计算当，时，与的大小关系是_________________．当，时，与的大小关系是_________________．●探究证明ABCOD如图所示，为圆O的内接三角形，为直径，过C作于D，设，BD=b．（1）分别用表示线段OC，CD；（2）探求OC与CD表达式之间存在的关系（用含a，b的式子表示）．●归纳结论根据上面的观察计算、探究证明，你能得出与的大小关系是：_________________________．●实践应用要制作面积为1平方米的长方形镜框，直接利用探究得出的结论，求出镜框周长的最小值．22．（本题满分10分）●观察计算:>，=.…………………2分ABCOD●探究证明：（1），∴…………………3分AB为⊙O直径,∴.，，\n∴∠A=∠BCD.∴△∽△.…………………4分∴.即,∴.…………………5分（2）当时,,=；时,,>．…………………6分●结论归纳:．………………7分●实践应用设长方形一边长为米,则另一边长为米,设镜框周长为l米，则≥．……………9分当,即（米）时,镜框周长最小．此时四边形为正方形时,周长最小为4米.………………10分〔2011•大理〕23．（8分）如图，点A、B、D、E在⊙O上，弦AE、BD的延长线相交于点C．若AB是⊙O的直径，D是BC的中点．（1）试判断AB、AC之间的大小关系，并给出证明；第23题O（2）在上述题设条件下，ΔABC还需满足什么条件，点E才一定是AC的中点？（直接写出结论）．第23题O23．解：(1)AB=AC【证法一】连结AD，∵AB是⊙O的直径∴∠ADB＝90°即AD⊥BC∵AD公用，BD=DC，∴Rt△ABD≌Rt△ACD∴AB=AC【证法二】连结AD，则AD⊥BC\n又BD=DC，∴AD是线段BD的中垂线∴AB=AC(2)△ABC为正三角形，或AB=BC，或AC=BC，或∠A=∠B，或∠A=∠C(2011江西省)22.图甲是一个水桶模型示意图，水桶提手结构的平面图是轴对称图形，当点O到BC（或DE）的距离大于或等于⊙O的半径时（⊙O是桶口所在圆，半径为OA），提手才能从图甲的位置转到图乙的位置，这样的提手才合格.现用金属材料做了一个水桶提手（如图丙A-B-C-D-E-F，C-D是，其余是线段），O是AF的中点，桶口直径AF=34cm，AB=FE=5cm，∠ABC=∠FED=149°.请通过计算判断这个水桶提手是否合格.图丙ABCDEFO34BCAO图甲FEDBCAO图乙DEF（参考数据：≈17.72，tan73.6°≈3.40，sin75.4°≈0.97.）22．解法一连接OB，过点O作OG⊥BC于点G.………………1分在Rt△ABO中，AB=5，AO=17，∴tan∠ABO=，∴∠ABO=73.6°，………………4分∴∠GBO=∠ABC－∠ABO=149°－73.6°=75.4°.………………5分又∵，………………6分∴在Rt△OBG中，.……………8分∴水桶提手合格.……………9分解法二连接OB，过点O作OG⊥BC于点G.……………1分在Rt△ABO中，AB=5，AO=17，∴tan∠ABO=，∴∠ABO=73.6°.………………4分要使OG≥OA，只需∠OBC≥∠ABO，∵∠OBC=∠ABC－∠ABO=149°－73.6°=75.4°＞73.6°，……8分图丙ABCDEFO34G∴水桶提手合格.………………9分(2011江西省)21.如图，已知⊙O的半径为2，弦BC的长为，点A为弦BC所对优弧上任意一点（B，C两点除外）.（1）求∠BAC的度数；（2）求△ABC面积的最大值.ABCO（参考数据：，，.）\n21．解：(1)解法一连接OB，OC，过O作OE⊥BC于点E.∵OE⊥BC，BC=，∴.………………1分ABCOD在Rt△OBE中，OB=2，∵，∴,∴，∴.………………4分解法二连接BO并延长，交⊙O于点D，连接CD.∵BD是直径，∴BD=4，.在Rt△DBC中，,∴，∴.………………4分(2)解法一因为△ABC的边BC的长不变，所以当BC边上的高最大时，△ABC的面积最大，此时点A落在优弧BC的中点处.………………5分过O作OE⊥BC于E，延长EO交⊙O于点A，则A为优弧BC的中点.连接AB，AC，则AB=AC，.ABCOE在Rt△ABE中，∵，∴，∴S△ABC=.答：△ABC面积的最大值是.………………8分解法二因为△ABC的边BC的长不变，所以当BC边上的高最大时，△ABC的面积最大，此时点A落在优弧BC的中点处.………………5分过O作OE⊥BC于E，延长EO交⊙O于点A，则A为优弧BC的中点.连接AB，AC，则AB=AC.∵,∴△ABC是等边三角形.………………6分在Rt△ABE中，∵，∴，∴S△ABC=.答：△ABC面积的最大值是.………………8分\n第21题ABOCD23．（2011·漳州）（满分10分）如图，AB是⊙O的直径，＝，∠COD＝60°．（1）△AOC是等边三角形吗？请说明理由；（2）求证：OC∥BD．【答案】说明：其他证明酌情给分解（1）△AOC是等边三角形………………1分第21题ABOCD1证明：∵＝，∴∠1＝∠COD＝60°………………3分∵OA＝OC，∴△AOC是等边三角形………………5分（2）证法一：∵＝，∴OC⊥AD………………7分又∵AB是⊙O的直径，∴∠ADB＝90°，即BD⊥AD………………9分∴OC∥BD………………10分证法二：∵＝，∴∠1＝∠COD＝∠AOD………………7分又∠B＝∠AOD∴∠1＝∠B………………9分∴OC∥BD………………10分