- 282.50 KB
- 2022-07-20 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
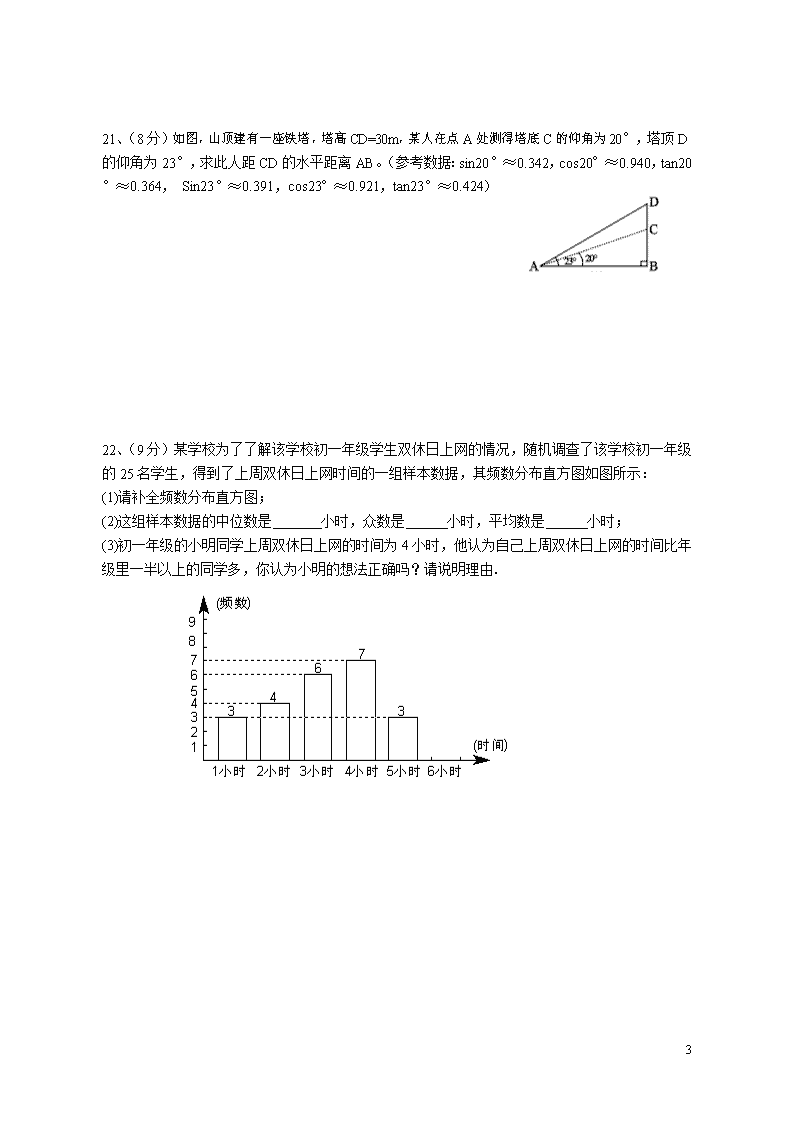
泰兴市珊瑚初中初三数学假期作业拟卷:袁鋆2013.4.26一、填空题(每题3分,共36分)1、的相反数是()A.B.C.D.2、今年1-2月份,我市经济发展形势良好,已完成的固定资产投资快速增长,达240.31亿元,用科学记数法可记作()元。A.B.C.D.ABCD40°120°(第3题)3、如图,在△ABC中,D是BC延长线上一点,∠B = 40°,∠ACD = 120°,则∠A等于A.60°B.70°C.80°D.90°4、当时,二次根式的值为()A.1B.±1C.3D.±35、已知抛物线y=ax2+2ax+4(0x2,且x1+x2=1-a,则()A.y1y2D.y1与y2的大小不能确定6如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连结EG、OF.则∠OFG的度数是()A.60°B.45°C.30°D.75°7、如图,在梯形ABCD中,AB//DC,∠D=90o,AD=DC=4,AB=1,F为AD的中点,则点F到BC的距离是()A.2B.4C.8D.18.已知:如图,Rt△ABC外切于⊙O,切点分别为E、F、H,∠ABC=90o,直线FE、CB交于D点,连结AO、HE,则下列结论:①∠FEH=45o+∠FAO②BD=AF③AB2=AO×DF④AE×CH=S△ABC其中正确的是().A.①②③④B.①③④C.②③④D.①②③二、填空题(每题3分,共10分)9、因式分解:。10、现有4条线段,长度分别为,,,,从中任取条,能构成三角形的概率是。8\n11、如图,是的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是.12、等腰三角形的腰长为2,腰上的高为1,则它的底角等于.13.用圆心角为,半径为的扇形做成一个无底的圆锥侧面,则此圆锥的底面半径为.14.在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交BC于点E,过点A作直线CD的垂线交CD于点F,若AB=4,BC=6,则CE+CF的值为;15..已知△ABC中,AC=BC=8,∠ACB=90°,D是直线AC上一点,CD:AC=1:2,折叠△ABC,使B落在D点上,则折痕长为.yxO16、如图,点A,B的坐标分别为(1,4)和(4,4),抛物线的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为,则点D的横坐标最大值为(第11题)(第16题)(第18题)17.在△ABC中,∠A=40º,△ABC绕点A旋转后点C落在边AB上的点C’,点B落到点B’,如果点C、C’、B’在同一直线上,那么∠B的度数是▲.18、如图,点为直线上的两点,过两点分别作y轴的平行线交双曲线()于两点.若,则的值为.三、解答题(共96分)19、(6分)解不等式组并写出该不等式组的整数解.20、(8分)请你先化简,再从-2,2,中选择一个合适的数代入求值.8\n21、(8分)如图,山顶建有一座铁塔,塔高CD=30m,某人在点A处测得塔底C的仰角为20°,塔顶D的仰角为23°,求此人距CD的水平距离AB。(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,Sin23°≈0.391,cos23°≈0.921,tan23°≈0.424)22、(9分)某学校为了了解该学校初一年级学生双休日上网的情况,随机调查了该学校初一年级的25名学生,得到了上周双休日上网时间的一组样本数据,其频数分布直方图如图所示:(1)请补全频数分布直方图;(2)这组样本数据的中位数是小时,众数是小时,平均数是小时;(3)初一年级的小明同学上周双休日上网的时间为4小时,他认为自己上周双休日上网的时间比年级里一半以上的同学多,你认为小明的想法正确吗?请说明理由.8\n23、(8分)如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,连结AC,过点O作AC的垂线交AC于点D,交⊙O于点E.已知AB﹦8,∠P=30°.(1)求线段PC的长;(2)求阴影部分的面积.24、(10分)如图1,某容器由A、B、C三个长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是容器容积的(容器各面的厚度忽略不计).现以速度v(单位:cm3/s)均匀地向容器注水,直至注满为止.图2是注水全过程中容器的水面高度h(单位:cm)与注水时间t(单位:s)的函数图象.Ot/sh/cm101812图2⑴在注水过程中,注满A所用时间为______s,再注满B又用了_____s;⑵求A的高度hA及注水的速度v;图1ABC⑶求注满容器所需时间及容器的高度.8\n25、(10分)在正方形ABCD中,O是AD的中点,点P从A点出发沿A→B→C→D的路线匀速运动,移动到点D时停止。(1)如图1,若正方形的边长为12,点P的运动速度为2单位长度/秒,设t秒时,正方形ABCD与∠POD重叠部分的面积为y。①求当t=4,8,14时,y的值。②求y关于t的函数解析式。(2)如图2,若点Q从D出发沿D→C→B→A的路线匀速运动,移动到点A时停止。P、Q两点同时出发,点P的速度大于点Q的速度。设t秒时,正方形ABCD与∠POD(包括边缘及内部)重叠部分的面积为S,S与t的函数图像如图3所示。①P,Q两点在第秒相遇;正方形ABCD的边长是②点P的速度为单位长度/秒;点Q的速度为③当t为何值时,重叠部分面积S等于9?8\n26、(12分)已知:在矩形A0BC中,分别以OB,OA所在直线为轴和轴,建立如图所示的平面直角坐标系.E是边AC上的一个动点(不与A,C重合),过E点的反比例函数的图象与BC边交于点F.(1)若△OAE、△OBF的面积分别为S1、S2且S1+S2=2,求k的值;(2)若OB=4,OA=3,记问当点E运动到什么位置时,S有最大值,其最大值为多少?(3)请探索:是否存在这样的点E,使得将△CEF沿EF对折后,C点恰好落在OB上?若存在,求出点E的坐标;若不存在,请说明理由.8\n27(本题12分)在平面直角坐标系xOy中,抛物线与y轴交于点B,其顶点A在直线上运动。(1)当时,求点B的坐标;(2)当△AOB为直角三角形时,求b、c的值;(3)已知△CDE的三个顶点的坐标分别为C(-5,2),D(-3,2),E(-5,6),当抛物线对称轴左侧的部分与△CDE的三边一共有两个公共点时,求b的取值范围。ABxyOABxyO8\n28.(本题14分)如图1,在平面直角坐标系xOy中,点A,B坐标分别为(8,4),(0,4),线段CD在于x轴上,CD=3,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E,交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.(1)求线段CE的长;(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t函数关系式及t的取值范围;(3)如图2,连结DF,当t取何值时,以C,F,D为顶点的三角形为等腰三角形?图2图1直接写出ΔCDF的外接圆与OA相切时t的值.8