- 669.36 KB
- 2022-07-20 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
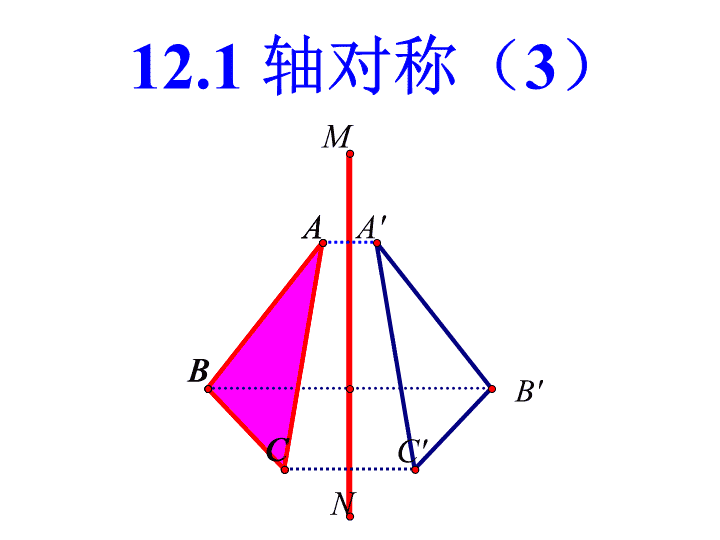
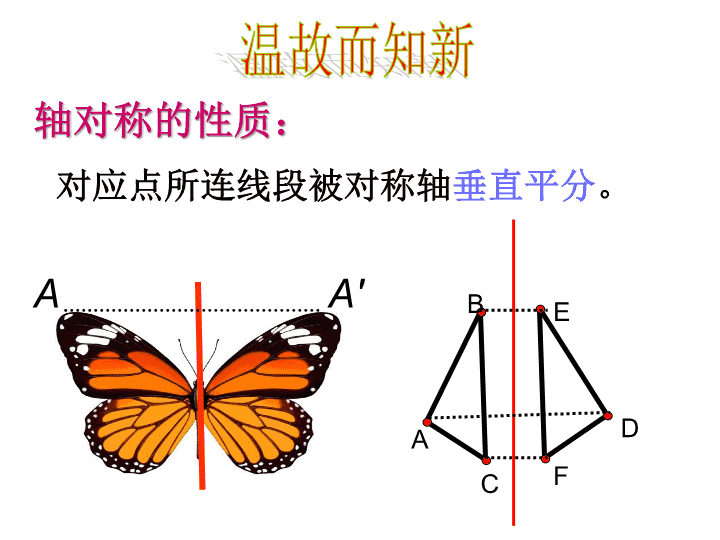
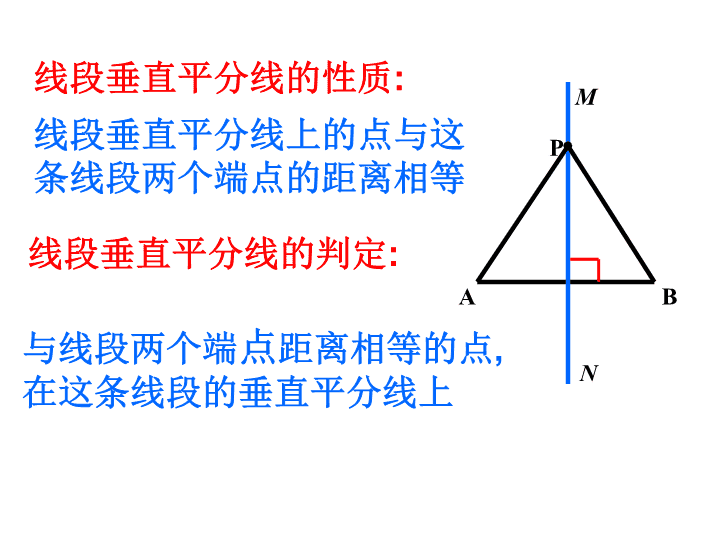
12.1轴对称(3)C'A'CAACBBMNB'\n轴对称的性质:对应点所连线段被对称轴垂直平分。温故而知新BACEDFAA'\n线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等线段垂直平分线的判定:与线段两个端点距离相等的点,在这条线段的垂直平分线上ABPMN\n问题(一)如何作轴对称图形的对称轴?作出对应点所连线段的垂直平分线1.如图,点A和点B关于某条直线成轴对称,你能作出这条对称轴吗?AB\n问题(二)如何作出线段的垂直平分线?(经过线段中点并且垂直于这条线段的直线)根据线段的垂直平分线的定义:(1)找出线段中点.(2)过中点作这条线段的垂线.如何用尺规作图法作出线段的垂直平分线?思考:提示:由两点确定一条直线和线段的垂直平分线的性质,只要作出到线段两端点距离相等的两个点即可.\n1.如图,点A和点B关于某条直线成轴对称,你能作出这条对称轴吗?AB⑴分别以点A、B为圆心,以大于于AB的长为半径作弧,两弧相交于C、D两点;⑵作直线CDCD即为所求的直线。CD作法:\nABCA′B′C′MNP2.△ABC与△A′B′C′关于某条直线对称,请你作出它的对称轴。MN就是它们的对称轴。\n如何作出五角星的对称轴?思考分析:只要找到任意一组对应点,作出这对对应点连线的垂直平分线,就可以得到此图形的对称轴.\nAA1A2作法:1.找出五角星的一对对应点A、A1,连接AA12.作出线段AA1的垂直平分线A3A2A3就是一条对称轴。五角星共有几条条对称轴?\n1.有时我们感觉两个图形是轴对称,如何验证?2.如图,△ABC与△DEF关于某条直线成轴对称吗?归纳:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。BACEDF用这种方法可以判定两个图形是否关于某条直线对称。思考:\n1.作出下列图形的对称轴2无数条213试一试\nMMNN2.与图A成轴对称的是哪个图形?画出它的对称轴。B\n谈谈你的收获1、用尺规作图作已知线段的垂直平分线;2、用作垂直平分线的方法作轴对称图形或成轴对称的两个图形的对称轴;3、验证图形是否是轴对称图形或是否成轴对称。\n线段是轴对称图形.它有两条对称轴,分别为:线段的中垂线,线段本身所在的直线.线段是不是轴对称图形?\nOABC角是轴对称图形,对称轴是角平线所在的直线.角是不是轴对称图形?\n两相交直线是不是轴对称图形?\n如图甲,△ABC和△A′B′C′关于直线L对称,延长对应线段AC和A′C′,两条延长线相交吗?交点与对称轴L有什么关系?延长其他对应线段呢?在图乙中,AC与A′C′又如何呢?再找几个成轴对称的图形观察一下,能发现什么规律吗?结论:成轴对称的两个图形,对应线段的延长线如果相交,交点一定在对称轴上;对应线段的延长线如果不相交,也就是对应线段所在的直线平行,那么它们也与对称轴平行.