初中数学课件4.2证明 18页

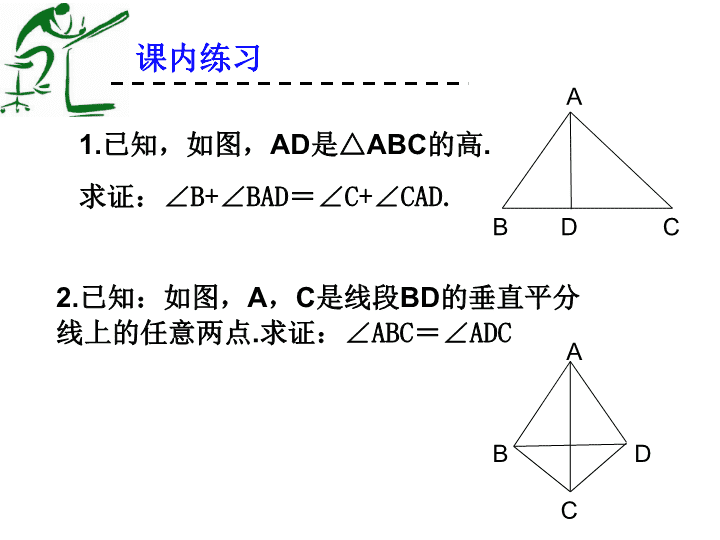
4.2证明(3)\nBDCAO证明：（1）∵AD是∠BAC的平分线（已知）∴∠BAO＝∠CAO（角平分线的定义）.∵　BC⊥AD（已知），∴　∠AOB＝∠AOC＝Rt∠(垂线的定义).又∵　AO＝AO（公共边），∴　△ABO≌△ACO（ASA）.∴　AB＝AC（全等三角形的对应边相等）.∴　△ABC是等腰三角形（等腰三角形的定义）例4　已知：如图，AD是∠BAC的平分线，BC⊥AD于点O，AC⊥DC于点C，求证：（1）△ABC是等腰三角形；(2)∠D=∠B.（2）∵　AC⊥DC（已知），∴　∠D+∠CAD＝90º（直角三角形的两个锐角互余）.∵　BC⊥AD（已知），∴　∠B+∠BAD＝90º（直角三角形的两个锐角互余）.∵　∠BAD＝∠CAD（角平分线的定义），∴　∠B＝∠D（等角的余角相等）.\n课内练习1.已知，如图，AD是△ABC的高.求证：∠B+∠BAD＝∠C+∠CAD.ABDC2.已知：如图，A，C是线段BD的垂直平分线上的任意两点.求证：∠ABC＝∠ADCBDCA\n已知命题：如图，点A，D，B，E在同一直线上，且AD＝BE，AC∥DF，则△ABC≌△DEF.这个命题是真命题还是假命题？ADBECF如果是真命题，请给出证明；如果是假命题，请添加适当的条件，使它成为真命题.你有几种不同的添加方法？\n知识与回顾:你会判定两个三角形全等吗?有哪些方法?(1)SSS(2)SAS(3)ASA(AAS)(4)HL(用于两个直角三角形全等的判定)\n例5已知:如图,AD是△ABC的高,E是AD上一点.AD=BD,DE=DC,求证:∠1=∠C.⌒BCDE1∟A想一想:(1)由已知AD是△ABC的高,可以得到什么?(2)由已知AD=BD,DE=DC,∠BDE=Rt∠=∠ADC,可以得到什么结论?(3)据此,你能得到∠1=∠C吗?\n例5已知:如图,AD是△ABC的高,E是AD上一点.AD=BD,DE=DC,求证:∠1=∠C.A⌒BCDE1∟证明:∵AD是△ABC的高,E是AD上一点(已知)∴∠BDE=Rt∠=∠ADC又∵BD=AD(已知)DE=DC(已知)∴△BDE≌△ADC∴∠1=∠C(全等三角形的对应角相等)(SAS)\n小收获:要证明一个结论,可以从已知出发,推出可能的结果,并与证明的结论比较,直至推出要证明的结论.\n学以致用:已知:如图,在△ABC中,D,E分别是AB,AC上的点,∠1=∠2.求证:∠B=∠ADE）（ABCDE12\n学以致用:已知:如图,AD∥BC,∠B=∠D.求证:△ADC≌△CBA.ABCD\n例6已知:如图,AD是三角形纸片ABC的高.将纸片沿直线EF折叠,使点A和点D重合.求证:EF∥BC.ABCDEF知识加油站:(1)由将纸片沿直线EF折叠,使点A和点D重合可知,点A和点D关于直线EF_______(2)对称轴是______(3)由此可得,EF与AD有怎样的位置关系?_________轴对称直线EFEF⊥AD\n例6已知:如图,AD是三角形纸片ABC的高.将纸片沿直线EF折叠,使点A和点D重合.求证:EF∥BC.ABCDEFBC⊥AD()已知EF⊥AD只需证要证EF∥BCEF是AD的对称轴点A与点D重合(已知)探讨证明的思路:\n例6已知:如图,AD是三角形纸片ABC的高.将纸片沿直线EF折叠,使点A和点D重合.求证:EF∥BC.ABCDEF证明:因为将纸片沿直线EF折叠时,点A与点D重合,所以EF是线段AD的对称轴,∴EF⊥AD(对称轴垂直平分连结两个对称点之间的线段)∵AD是△ABC的高(已知)∴BC⊥AD(三角形的高的定义)(在同一平面内,垂直于同一条直线的两条直线平行)∴EF∥BC\n又有了收获:从要证明的结论出发,探索要使结论成立,需要什么条件,并与已知对照,充分利用已知条件,直至找到需要,并且这个最后的需要是已知的条件,从而达到证明的目的.\n学以致用:已知:如图,在四边形ABCD中,AD=BC,AB=CD.求证:AB∥CD,AD∥BC.ABCD\n设计题:你听说过费马点吗?如图,P为△ABC所在平面上的一点.如果∠APB=∠BPC=∠CPA=120,则点P就是费马点.费马点有许多有趣并且有意义的性质,例如,平面内一点P到△ABC三顶点的距离之和为PA+PB+PC,当点P为费马点时,距离之和最小.假设A,B,C表示三个村庄,要选一处建车站,使车站到三个村庄的公路路程的和最短.若不考虑其他因素,那么车站应建在费马点上.请按下列步骤对费马点进行探究:(1)查找有关资料,了解费马点被发现的历史背景;(2)在特殊三角形中寻找并验证费马点.例如,当△ABC是等边三角形,等腰三角形或直角三角形时,费马点有哪些性质?(3)把你的探究结果写成一篇小论文,并通过与同学交流来修改完善你的小论文.(课本第82页)ABCP\n学有所成本节课你学到什么？\n学有所成布置作业:(1)课本81页第1,3,4,5题;第6题选做.(2)见作业本再见