- 615.60 KB
- 2022-07-20 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
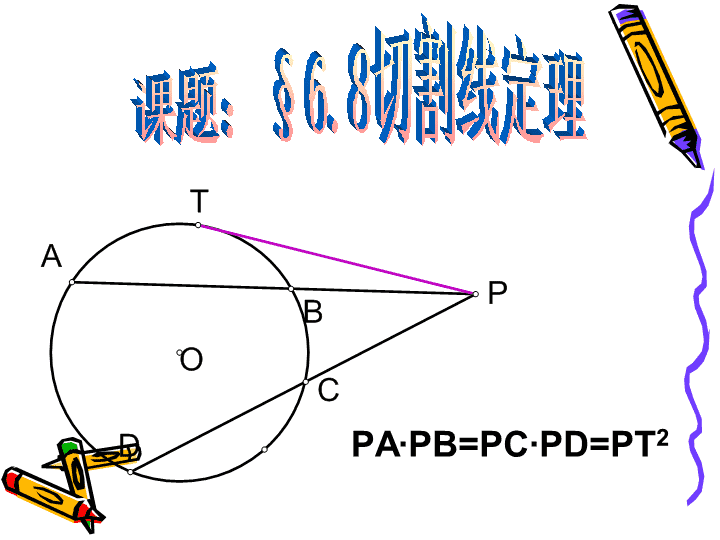
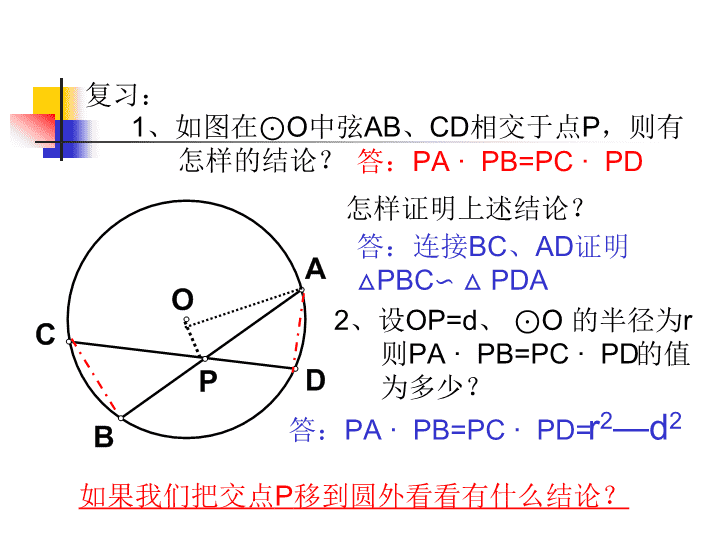
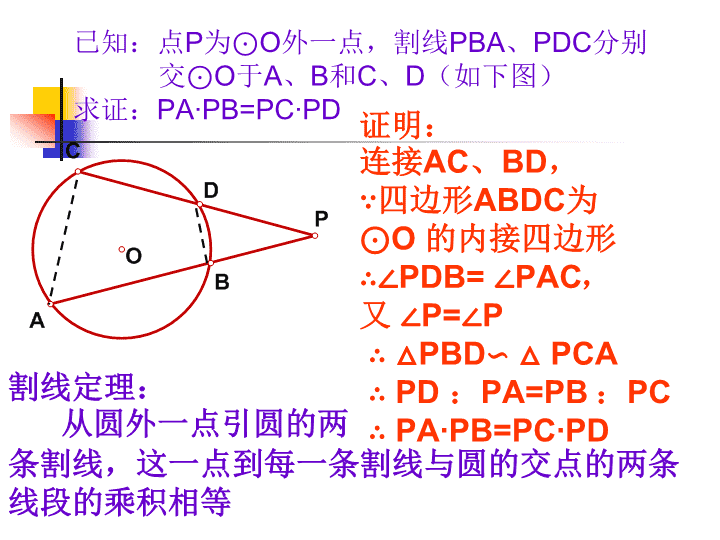
课题:§6.8切割线定理PA∙PB=PC∙PD=PT2\n复习:1、如图在⊙O中弦AB、CD相交于点P,则有怎样的结论?答:PA∙PB=PC∙PD怎样证明上述结论?答:连接BC、AD证明△PBC∽△PDA答:PA∙PB=PC∙PD=r2—d2如果我们把交点P移到圆外看看有什么结论?2、设OP=d、⊙O的半径为r则PA∙PB=PC∙PD的值为多少?\n已知:点P为⊙O外一点,割线PBA、PDC分别交⊙O于A、B和C、D(如下图)求证:PA∙PB=PC∙PD证明:连接AC、BD,∵四边形ABDC为⊙O的内接四边形∴∠PDB=∠PAC,又∠P=∠P∴△PBD∽△PCA∴PD:PA=PB:PC∴PA∙PB=PC∙PD割线定理:从圆外一点引圆的两条割线,这一点到每一条割线与圆的交点的两条线段的乘积相等\nPA∙PB=PC∙PDPA∙PB=PC∙PD点P从圆内移动到远外点C、D重合为一点会有什么结论?答:PC2=PA∙PB怎样证明结论?\n已知:(如图)点P为⊙O外一点,PC切⊙O于点C,割线PBA交⊙O于A、B求证:PC2=PA∙PB证明:连接AC、BC,∵PC切⊙O于点C∴∠B=∠PCA,又∠P=∠P∴△PCA∽△PBC∴PC:PA=PB:PC∴PC2=PA∙PB切割线定理:从圆外一点引圆的两切线和条割线,切线长是这点到割线与圆的交点的两条线段长的比例中项。\nAB交CD于点=>PA∙PB=PC∙PDPC切⊙O于点C点=>PA∙PB=PC∙PD割线PCD、PAB交⊙O于点C、D和A、B=>PA∙PB=PC∙PD思考:从这几个定理的结论里大家能发现什么特征?结论都为乘积式几条线段都是从同一点出发都是通过三角形相似来证明(都隐含着三角形相似)我们学过的定理中还有结论为乘积式的吗?\n已知:(如图)过⊙O外一点P作两条割线,分别交⊙O于点A、B和C、D,再作⊙O的切线PE,E为切点,连接CE、DE。已知AB=3cm,PA=2cm,CD=4cm.(1)求PC的长(2)设CE=a,试用含a的代数式表示DE。解:(1)由切割线定理,得PE2=PC∙PD=PA∙PB∵AB=3cm,PA=2cm∴PB=AB+PA=5(cm)∵CD=4cm∴PD=PC+CD=PC+4∴PC(PC+4)=2X5化简,整理得:PC2+4PC−10=0解得:(负数不合题意,舍去)\n例2:(如图)A是⊙O上一点,过A切线交直径CB的延长线于点P,AD⊥BC,D为垂足。求证:PB:PD=PO:PC。分析:要证明PB:PD=PO:PC很明显PB、PD、PO、PC在同一直线上无法直接用相似证明,且在圆里的比例线段通常化为乘积式来证明,所以可以通过证明PB•PC=PD•PO,而由切割线定理有PA2=PB•PC只需再证PA2=PD•PO,PA为切线所以连接PO由射影定理得到。\n如图:过点A作⊙O的两条割线分别⊙O交于B、C和D、E。已知AD=4,DE=5,AB=BC,求AB、BD如图:A、B两点在x轴上原点的右边,点A在点B的左边,经过A、B两点的⊙C与y轴相切于点D(0,-3),如果AB=4(1)求A、B两点的坐标(2)求圆心C的坐标\n点P在圆内,r>d,此时,P到A、B的距离的乘积为PA∙PB=r2-d2点P在圆外,d>r,此时,P到A、B的距离的乘积为PA∙PB=d2-r2PA∙PB=|d2-r2|\n课堂小结1、这节课我们学习了切割线定理及推论(割线定理),要特别注意它与相交弦定理之间的联系与区别。2、要注意圆中的比例线段的结论的特点及实际中的用。3、圆中的比例线段在实际应用中也非常重要,注意与代数、几何等知识的联系及应用