初中数学中考专题复习《探究式问题以及课题学习专题 5页

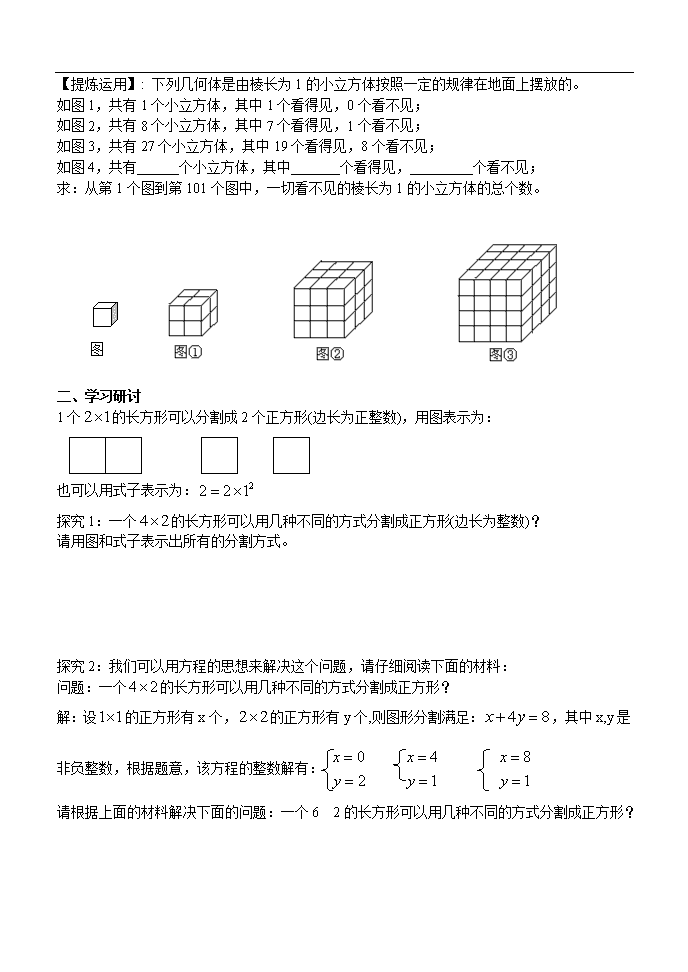
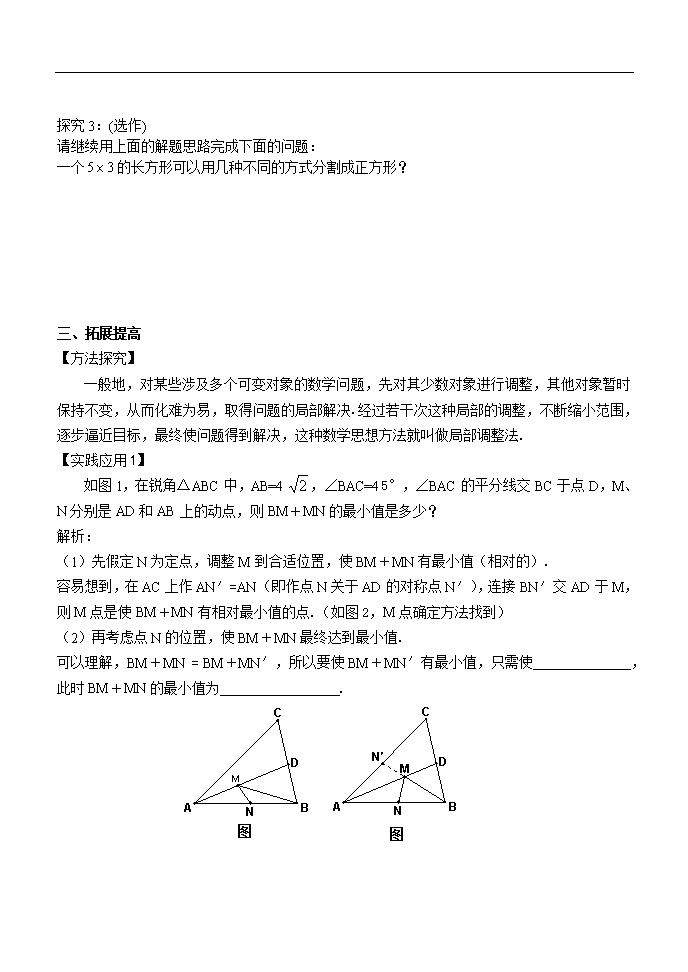
年级：九年级学科：数学执笔人：总第课时课题：《探究式问题以及课题学习专题》课型：复习课时间：1学习目标：主要复习数形结合、由特殊到一般、化归以及建模等数学思想，涉及到图形变换、综合探究、阅读理解等综合题，培养学生掌握解决此类问题的方法，提高学生对数学知识的综合应用能力以及应用数学知识解决实际问题的能力。复习重点：数学思想的确立，达到能够学以致用，融会贯通的程度。复习难点：使学生自己形成解决综合题目的方法和策略。学法指导：同学们可以先复习基础的探究知识，包括几何图形的基本运动和变换，找规律的内容，基本的作图等，想一想这些知识的内在联系以及各自可以用来解决什么样的数学问题，蕴藏着怎样的数学思想，再解决23题这样的探究综合性题目就有了一定的基础，加油呀！一、预习导学我们初中数学里的一些代数公式，很多都可以通过表示几何图形的面积的方法进行直观的推导和解释，例如：平方差公式，完全平方公式。BACD1212【提出问题】：如何用表示几何图形的面积的方法推证：【解决问题】：A表示1个的正方形，即：B表示1个的正方形，C和D恰好可以拼成1个的正方形因此，B,C,D就可以表示2个的正方形，即，因此A,B,C,D恰好可以拼成1个的大正方形由此可得：【递进探究】请仿用上面的表示几何图形面积的方法探究：要求：自己构造图形并写出详细的解题过程【推广研究】：请用上面的表示几何图形面积的方法探究：(参考公式：)\n【提炼运用】:下列几何体是由棱长为1的小立方体按照一定的规律在地面上摆放的。如图1，共有1个小立方体，其中1个看得见，0个看不见；如图2，共有8个小立方体，其中7个看得见，1个看不见；如图3，共有27个小立方体，其中19个看得见，8个看不见；如图4，共有______个小立方体，其中_______个看得见，_________个看不见；求：从第1个图到第101个图中，一切看不见的棱长为1的小立方体的总个数。图二、学习研讨1个的长方形可以分割成2个正方形(边长为正整数)，用图表示为：也可以用式子表示为：探究1：一个的长方形可以用几种不同的方式分割成正方形(边长为整数)？请用图和式子表示出所有的分割方式。探究2：我们可以用方程的思想来解决这个问题，请仔细阅读下面的材料：问题：一个的长方形可以用几种不同的方式分割成正方形？解：设的正方形有x个，的正方形有y个,则图形分割满足：，其中x,y是非负整数，根据题意，该方程的整数解有：请根据上面的材料解决下面的问题：一个62的长方形可以用几种不同的方式分割成正方形？\n探究3：(选作)请继续用上面的解题思路完成下面的问题：一个的长方形可以用几种不同的方式分割成正方形？三、拓展提高【方法探究】一般地，对某些涉及多个可变对象的数学问题，先对其少数对象进行调整，其他对象暂时保持不变，从而化难为易，取得问题的局部解决.经过若干次这种局部的调整，不断缩小范围，逐步逼近目标，最终使问题得到解决，这种数学思想方法就叫做局部调整法.【实践应用1】如图1，在锐角△ABC中，AB=4，∠BAC=45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM＋MN的最小值是多少？解析：（1）先假定N为定点，调整M到合适位置，使BM＋MN有最小值（相对的）.容易想到，在AC上作AN′=AN（即作点N关于AD的对称点N′），连接BN′交AD于M，则M点是使BM＋MN有相对最小值的点.（如图2，M点确定方法找到）（2）再考虑点N的位置，使BM＋MN最终达到最小值.图1图2可以理解，BM＋MN=BM＋MN′，所以要使BM＋MN′有最小值，只需使，此时BM＋MN的最小值为.\n【实践应用2】如图，把边长是3的正方形等分成9个小正方形，在有阴影的两个小正方形内（包括边界）分别任取点P、R，与已知格点Q（每个小正方形的顶点叫做格点）构成三角形，则△PQR的最大面积是，请在图2中画出面积最大时的△PQR的图形.图1图2备用图四、小结请结合本节课的学习，谈谈自己在解决探究性问题时有什么要注意的问题，有什么样的解题策略？五、课后作业1、把边长为3的正三角形各边三等分，分割得到图①，图中含有1个边长是1的正六边形；把边长为4的正三角形各边四等分，分割得到图②，图中含有3个边长是1的正六边形；把边长为5的正三角形各边五等分，分割得到图③，图中含有6个边长是1的正六边形；…依此规律，探究1：把边长为7的正三角形各边七等分，并按同样的方法分割，得到的图形中含有个边长是1的正六边形．\n…图①图②图③探究2：把边长为n的正三角形各边n等分，并按同样的方法分割，得到的图形中含有多少个边长是1的正六边形？写出探究过程。2、升学指导1563、4、5、6