[中考数学课件]中考数学复习两圆的公切线3［人教版］ 17页

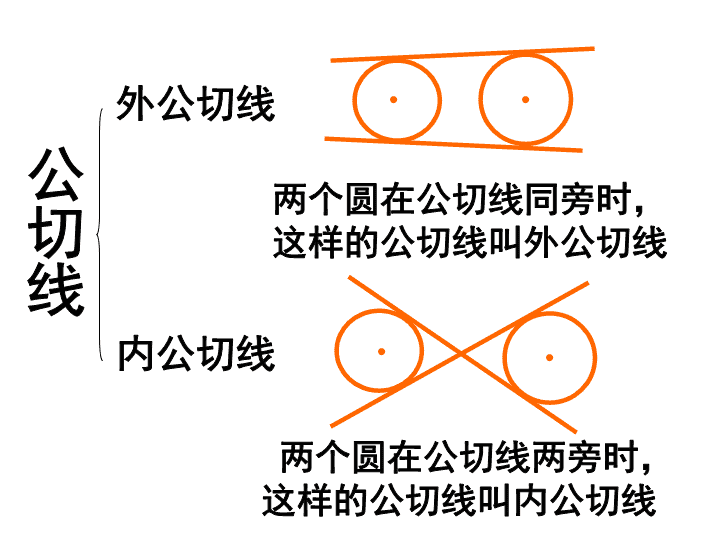
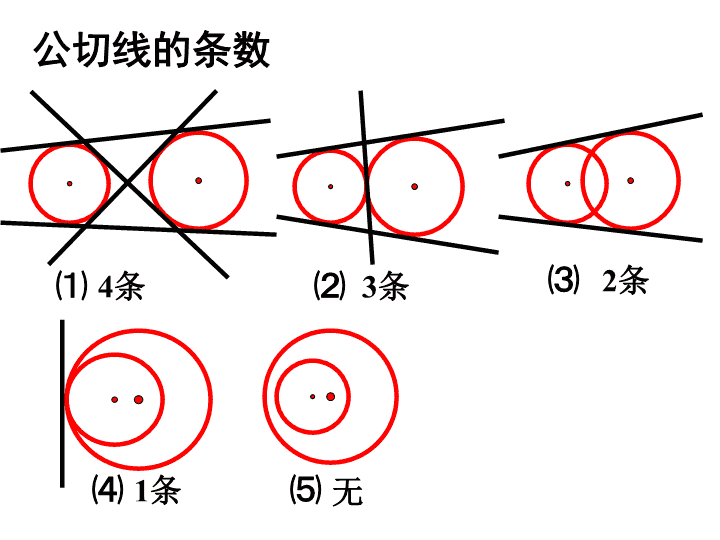
复习（八）两圆的公切线\nB外公切线内公切线两个圆在公切线同旁时，这样的公切线叫外公切线两个圆在公切线两旁时，这样的公切线叫内公切线公切线\n⑴⑵⑶⑷⑸4条3条2条1条无公切线的条数\n1、连结两圆心与两切点，构造出直角梯形；2、过一点做直角梯形的高,分成矩形和直角三角形；3、把求外公切线长转化为解直角三角形，利用解直角三角形的方法解决问题。外公切线内公切线解题思路\n设两圆的半径分别为R和r（R﹥r），圆心距为d，则两圆的外公切线长=（d﹥R-r）若两圆连心线与两圆外公切线的夹角为α，则sinα=\n（d﹥R+r）设两圆的半径分别为R和r（R﹥r），圆心距为d，则两圆的内公切线长=若两圆连心线与两圆内公切线的夹角为α，则sinα=\n1、已知:⊙01，⊙02的半径分别为2cm和3cm，它们切于点T。外公切线AB与⊙01、⊙02分别切于点A、B，则外公切线的长AB=。检测练习\n2、已知:⊙01，⊙02外切于点C，直线AB分别切⊙01，⊙02于A、B两点，⊙02的半径为1，AB=，则⊙01的半径是。\n3.已知⊙O1的半径4cm，⊙O2的半径1cm，两圆的圆心距为6cm，那么两圆的外公切线长为，内公切线长为，连心线与外公切线的夹角为，连心线与内公切线夹角的正弦值是.\n4、已知⊙O1和⊙O2的外切于点P，AB切⊙O1于A，切⊙O2于B.⑴若连结PA、PB，求证：PA⊥PB.⑵若R1=5cm，R2=3cm，PQ⊥AB于Q，求PQ的长.QO1O2ABP\n引伸1.如图，⊙O1与⊙O2外切于点P，AB是两圆的公切线，切点为B，A.连结BP并延长交⊙O2于C，过C作AB的平行线交⊙O1于D，E.⑴求证：AC是⊙O1的直径；⑵试判断线段BD、BA、BE的大小关系，并证明.AO1O2BPCDE\n引伸2.如图甲,⊙O1与⊙O2外切于点P,AB是两圆的公切线,切点为B,A.直线AP,BP交⊙O1于C,⊙O2于D.AO1O2BPCD⑴求证：AB2=AD·BC⑵如图乙,当图甲中的切点P变为两圆的一个交点时,结论AB2=AD·BC还成立吗?若成立,请给出证明;若不成立,请说明理由.AO1O2BPCD\n5.如图⊙O1与⊙O2相交于A，B两点，AB的延长线与两圆的公切线CD交于点H，切点为C，D，AD交⊙O2于F，DB的延长线交⊙O1于E，EF交AB于G.⑴求证：AD·GB=HD·EB；AO1O2BCDHEFG⑵若CD=6，GF=1，求的值.EBGB\n课堂作业1.已知两等圆和另一个圆两两互相外切,且都与同一条直线相切,求等圆与另一个圆的半径之比.\nＢＣＡＯＭＮＰＸＹ2.圆心Ａ（０，３），⊙Ａ与Ｘ轴相切，⊙Ｂ的圆心在Ｘ轴的正半轴上，且⊙Ｂ与⊙Ａ外切于点Ｐ，两圆的公切线ＭＰ交Ｙ轴于点Ｍ，交Ｘ轴于Ｎ.(１).若sin∠OAB=0.8，求直线MP的解析式及经过M,N,B三点的抛物线的解析式\n(2)若⊙Ａ的位置大小不变，⊙Ｂ的圆心在Ｘ轴正半轴移动并使⊙Ａ与⊙Ｂ始终外切，过Ｍ作⊙Ｂ的切线ＭＣ，切点为Ｃ，在此变化过程中探究：①四边形ＯＭＣＢ是什么四边形，对你的结论加以证明．②经过Ｍ，Ｎ，Ｂ三点的抛物线上是否存在以ＢＮ为腰的等腰三角形？若存在，表示出来；若不存在，说明理由．\n3.以抛物线Y=X2的点(原点除外)为圆心且切X轴的动圆C,如果C的圆心是(a,a2),把这个圆记为C(a);如果C的圆心是(b,b2),把这个圆记为C(b);(1)试用a,b表示C(a),C(b)外切的条件.(2)在C(a)和C(b)外切只有一个的情况下,求a的值.