中考数学复习课件：实数 复习(共26张PPT) 26页

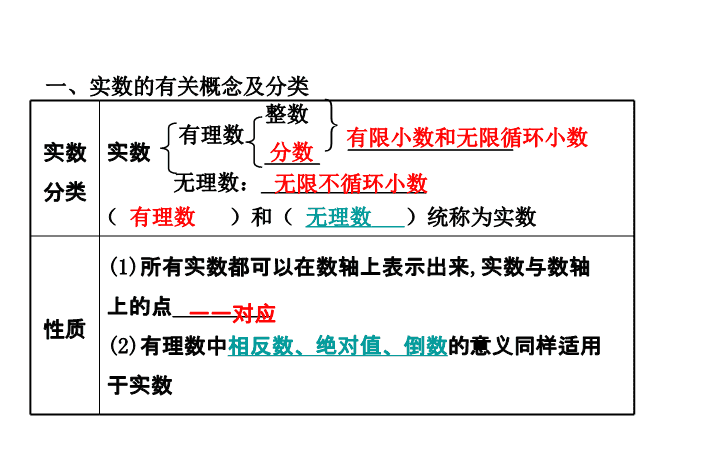
实　数\n一、实数的有关概念及分类实数分类实数性质(1)所有实数都可以在数轴上表示出来,实数与数轴上的点_________(2)有理数中相反数、绝对值、倒数的意义同样适用于实数有理数整数_____无理数：_______________分数无限不循环小数一一对应}_______________有限小数和无限循环小数（有理数）和（无理数）统称为实数\n二、实数的运算实数的运算种类实数的运算包括加、减、乘、除、乘方、_____开方运算(1)__________可以进行开平方运算(2)_________都可以进行开立方运算实数的运算顺序先算___________,再算_____,最后算_____,如果有括号,先算括号里面的零次幂及负整数指数幂a0=__(a≠0),a-n=____(a≠0,n是正整数)开方正实数及0任意实数乘方、开方乘除加减1\n实数的分类及有关概念【例1】下列各数：，π，，cos60°，0，，其中无理数的个数是()A.1个B.2个C.3个D.4个本题考查无理数的概念，判断时要紧扣概念，即无限不循环小数是无理数.B\n【真题专练】1.下列实数是无理数的是()A.-1B.0C.πD.【解析】选C.由无理数的定义，无限不循环小数是无理数，可知π是无理数.2.在实数中，有理数有()A.1个B.2个C.3个D.4个【解析】选D.分数和整数是有理数，故，0，=6，-1.414是有理数，共4个.\n平方根、立方根与算术平方根【例2】2的算术平方根是()A.±B.C.±4D.4(2)已知是二元一次方程组的解，则m+3n的立方根为_____________.B\n（1)选B.2的算术平方根是(2)把x=2，y=1代入二元一次方程组中，得解得∴m+3n=8，∴m+3n的立方根为2.答案：2\n(打“√”或“×”)1.-1是(-1)2的算术平方根.()2.1的平方根是它本身.()3.0没有算术平方根.()4.立方根等于本身的数有±1和0.()5.的立方根是3.()×××√×6.带根号的数都是无理数.()7.3<.()8.-2的相反数和绝对值都是2-.()××√\n1.8的平方根是()A.4B.±4C.D.±2.0.49的算术平方根的相反数是()A.0.7B.-0.7C.±0.7D.0DB3.的立方根是()A.-1B.0C.1D.±14.实数0.5的算术平方根等于()A.2B.C.D.CC\n5.=_________.【解析】利用22=4，可得=2.答案：26.4的平方根是_______.【解析】∵(±2)2=4，∴4的平方根是±2.答案：±2\n7.如图，正方形ODBC中，OC=1，OA=OB，则数轴上点A表示的数是_________.【解析】∵四边形ODBC为正方形，∴BC=OC=1，∠BCO=90°，根据勾股定理得OB=，以O为圆心，对角线OB的长为半径画弧，交负半轴于一点A，则A点表示的实数就是－.答案：－\n【例3-2】.四个实数－2，0，－，1中，最大的实数是()A.-2B.0C.-D.1【解析】选D.根据“正数大于0，负数小于0，正数大于一切负数”可知1最大.\n1.下列计算正确的是()A.-(-3)2=9B.=3C.-(-2)=1D.|-3|=-3【解析】选B．-(-3)2=-9，A项错误.因为33=27，所以=3，B项正确.-(-2)是指-2的相反数，应该是2，C项错误.|-3|表示的-3的绝对值，应该是3，D项错误.倒数、相反数、绝对值与数轴\n实数的运算及大小比较【例3-1】(1)计算：(2)计算：【思路点拨】(1)先运算绝对值、指数、负指数，再进行加减运算.(2)先运算正切值、绝对值、算术平方根、负指数，再进行加减运算.\n2.下列四个实数中，绝对值最小的数是()A.-5B.-C.1D.4【解析】选C.-5的绝对值是5，-的绝对值是，1的绝对值是1，4的绝对值是4，∵1＜＜4＜5，∴绝对值最小的数是1.3.的相反数是()A．－B．C．－D．C\n4.实数a，b在数轴上的位置如图所示，以下说法正确的是()A.a+b=0B.b＜aC.ab＞0D.|b|＜|a|【解析】选D.∵由数轴上a，b两点的位置可知，-2＜a＜-1，0＜b＜1∴a+b＜0，a＜b，ab＜0，｜b｜＜｜a｜，故选项D正确；选项A，B，C错误.故选D.\n5.设n为正整数，且n＜＜n+1，则n的值为()A.5B.6C.7D.8【解析】选D.，∴8＜＜9，∴8＜＜8+1，∴n=8.\n6.计算：【解析】原式\n若平行四边形的一边长为2，面积为，则此边上的高介于()A.3与4之间B.4与5之间C.5与6之间D.6与7之间【解析】选B.设平行四边形边长为2的边上的高为x.∵平行四边形的面积为，∴2x=，解得：，∴此边上的高介于4与5之间，故选B.\n1.规定用符号［x］表示一个实数的整数部分，例如［3.69］=3，［］=1，按此规定［－1］=_______．【解析】∵的整数部分是3，∴-1的整数部分是2，即［-1］=2.答案：2找规律题\n2.一组数：2，1，3，x，7，y，23，…，满足“从第三个数起，前两个数依次为a，b，紧随其后的数就是2a－b”，例如这组数中的第三个数“3”是由“2×2－1”得到的，那么这组数中y表示的数为_______．【解析】x=2×1-3=-1，y=2×(-1)-7=-9.答案：-9\n【典例】计算：错因分析题\n课堂小结通过这节课的学习你有所提高吗？\n相反数定义：只有（）不同的两个数叫做互为相反数，0的相反数是（）。表示：实数a的相反数是（）。性质:a和b互为相反数，则a+b=绝对值定义：数轴上表示a的点到原点的距离。记作|a|倒数定义：乘积为（）的两个数互为倒数。\n【规律方法】无理数常见的三种类型(1)开不尽的方根，如等.(2)特定结构的无限不循环小数，如0.303003000300003…(两个3之间依次多一个0).(3)含有π的绝大部分数，如2π.注意：判断一个数是否为无理数，不能只看形式，要看化简结果.如是有理数，而不是无理数.\n平方根和立方根的性质1.平方根的性质：正数a有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根.2.立方根的性质：一个数的立方根只有一个，正数的立方根是正数，负数的立方根是负数，0的立方根是0.