2019届中考数学复习 核心素养专题（二）课件 5页

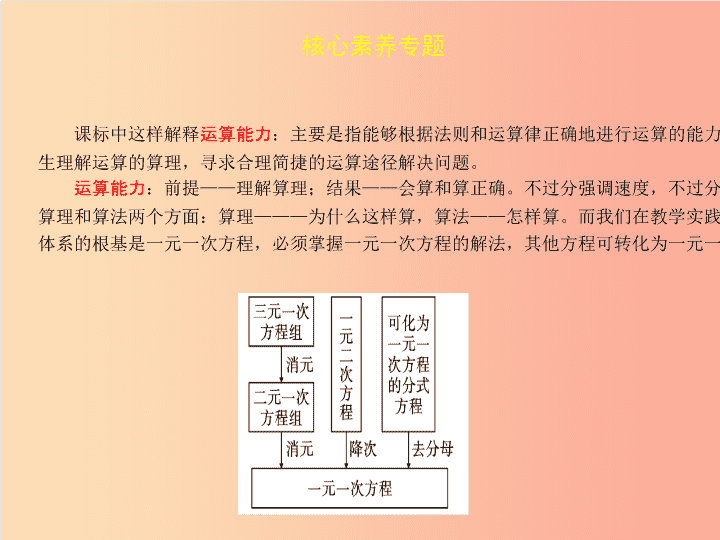
核心素养专题（二）\n初中数学学习各种方程，重点是根据具体问题中的数量关系列出方程，解决一些简单问题，并体会方程的模型思想，发展应用意识；为此还需要掌握各种方程的解法，提高运算能力和推理能力。有一种比较流行的说法：当今学生的运算能力大不如从前。这种说法所说的“运算能力”实际上更多指的是“计算技能”，强调的是“熟练程度”。就计算技能而言，可能真的今不如昔！这是计算技术进步的一个必然结果。当今智能化加速了这种趋势，我们要与时俱进。数学教育强调的是“运算能力”。核心素养专题\n核心素养专题课标中这样解释运算能力：主要是指能够根据法则和运算律正确地进行运算的能力。培养运算能力有助于学生理解运算的算理，寻求合理简捷的运算途径解决问题。运算能力：前提——理解算理；结果——会算和算正确。不过分强调速度，不过分强调技巧。数学运算包括算理和算法两个方面：算理———为什么这样算，算法——怎样算。而我们在教学实践中重算法，轻算理！方程体系的根基是一元一次方程，必须掌握一元一次方程的解法，其他方程可转化为一元一次方程。\n案例分析核心素养专题【例】阅读下面的材料，解答后面的问题。材料：解方程x4-3x2+2=0。解：设x2=y，原方程可变为y2-3y+2=0，即(y-1)(y-2)=0，解得y=1或y=2。当y=1时，即x2=1，解得x=±1；当y=2时，即x2=2，解得x=±。综上所述，原方程的解为x1=1，x2=-1，x3=，x4=-。问题：(1)上述解答过程采用的数学思想方法是()A.加减消元法B.代入消元法C.换元法D.待定系数法(2)采用类似的方法解方程：(x2-2x)2-x2+2x-6=0。\n【解】(1)C上述解答过程采用的数学思想方法是换元法。故选C。(2)设x2-2x=y，原方程可化为y2-y-6=0，即(y-3)(y+2)=0，解得y=3或y=-2。当y=3时，即x2-2x=3，解得x=-1或x=3；当y=-2时，即x2-2x=-2，此方程无解。综上所述，原方程的解为x1=-1，x2=3。核心素养专题