2013年江苏高考数学--品味高考,解密高考命题潜规则和解题技巧传播课件 58页

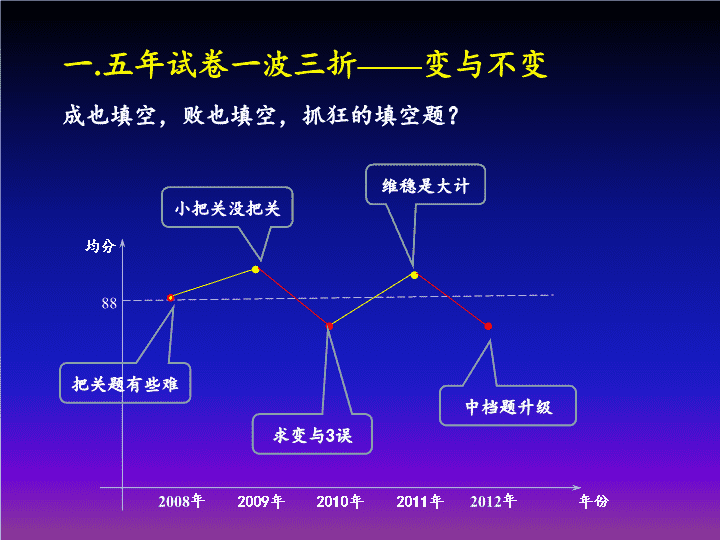
品味高考——感受江苏数学新高考张芙华\n二模后的安排原则：保温与冲刺阶段，以做为主，做中档题为主！(1)二模的反思与纠错——每人自查，反思30例解错的题(2)回归课本(立体几何定理，概率统计体系，应用题的格式规范，难题新题的课本背景、链接内容的了解)(3)创新题探究——3课15例，外加习题(4)典型试题再做——(10—2)(5)热身小练——6月的5个小练习时间紧迫，效率为先。抬头看路，埋头干活上周末，南京、苏州、常州、南通高三老师交流：\n年份均分2008年2009年2010年2011年2012年88把关题有些难小把关没把关求变与3误维稳是大计中档题升级一.五年试卷一波三折——变与不变成也填空，败也填空，抓狂的填空题？\n二.五年试卷各显特色1、2008年的话题：——小题多层把关——大把关是“组合问题”2、2009年的话题：——“创新”应用题压轴——平和常规的大题——填空题一马平川3、2010年的话题：——求变的后果——抓狂的填空题——三个“误区”\n二.五年试卷的特色4、2011年的话题：维稳大计——13题的无奈——20题“大”把关5、2012年的话题：——立体几何“把人留住”——应用大题提前把关——数列问题解法意外\n三.——变与不变1、填空题的三节：45分钟1——8的一望而知，一算即得9——12的中等要求细心别错13、14的小把关“事倍功半”2、解答题的三节：55分钟立几代数题把分送足解几应用题区别显著数列函数题“几舸”争流\n3、二卷加试：30分钟21(A，B，C，D)4选2当机立断22题中等要求应对熟练23题力求新意半易半难\n四.品数学高考的“五味”1、闯小关取舍休得两依依——酸2、送分的大题请您别客气——甜3、解几应用题还看真功夫——苦4、压轴的问题需要细品味——辣5、廿三题怎一个抢字了得——辛\n1、品味小题把关例1、函数y=x2(x>0)的图像在点(ak,，ak2)处的切线与x轴交点的横坐标为ak+1，其中k∈N*，若a1=16，则a1+a3+a5的值是．——切线斜率是导数，点斜式得切线方程，横截距是数列递推，等比数列，求和——6年江苏考了3次，06、10、11三年在知识网络的交汇处命题在知识网络的交汇处、绵绵不断的“链”\n例2、在平面直角坐标系xOy中，已知点P是函数f(x)=ex(x＞0)的图象上的动点，该图象在P处的切线l交y轴于点M，过点P作l的垂线交y轴于点N，设线段MN的中点的纵坐标为t，则t的最大值是_____．——设点(u,eu)，求导，切线方程，求M，求法线方程，求N，中点纵坐标t=g(u)，求函数t=g(u)的最值\n例3、设定义在区间(0，π/2)上的函数y=6cosx的图像与y=5tanx的图像的交于点P，过点P作x轴的垂线，垂足为P1，直线PP1与函数y=sinx的图像交于点P2，则线段P1P2的长为．——啰嗦的文字叙述许多，本质是什么？由6cosx=5tanx求sinx……打的是擦边球！这样审读与基本技能的情景你会是怎样的？\n例4、在锐角△ABC，A、B、C的对边分别为a、b、c，若b/a+a/b=6cosC，则tanC/tanA+tanC/tanB=．——方法：两边夹夹余弦定理，化边为角，化切为弦a2+b2=6abcosC，c2=4abcosC，sin2C=4sinAsinBcosC——三角变换不是容易题，但三角变形总能难住一部分……\n用方程组还是用角相关？三角变形总能难住一部分……\n例5、设1≤a1≤a2≤…≤a7，其中a1，a3，a5，a7成公比为q的等比数列，a2，a4，a6成公差为1的等差数列，则q的最小值是____．——a1，a2，a1q，a2+1，a1q2，a2+2，a1q3，…——找不到切入点，坚持还是放弃？非常方法难难你…\n例6、设实数x，y满足3≤xy2≤8，4≤x2/y≤9，则x3/y4的最大值是．——构造还是化归“非”常用方法难你……\n\n例7、设集合A={(x，y)|m/2≤(x－2)2+y2≤m2，x，y∈R}，B={(x，y)|2m≤x+y≤2m+1，x，y∈R}，若A∩B≠Φ，则实数m的取值范围是____．——分类、图形的动态分析2012年12、在平面直角坐标系xOy中，圆C的方程为x2+y2－8x+15=0，若直线y=kx－2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值为____．——空间想象、化归为本质数和形的转换…\n数和形的转换…\n例、将边长为1m的正三角形薄铁皮沿一条平行于某边的直线剪成两块，其中一块是梯形，记s=，则s的最小值是▲．x常模！\n例．设{an}是公比为q的等比数列，|q|＞1，令bn=an+1(n=1,2,…)，若数列{bn}有连续四项在集合{－53，－23，19，37，82}中，则6q=.【解析】将各数按照绝对值从小到大排列，各数减1，观察即可得解.——18，－24，36，－54，81思考：填空题怎么把关？恰到好处…\n思考：填空题怎么把关？1、知识网络的交汇处命题2、逻辑思维链加长型3、语境、情景掩盖本质，转化化归4、动态的图形分析、分类5、需建立数学模型解题6、探究型问题\n2、送分的大题请您别客气求解问题的表述要说清楚方法、依据、结果大题的解答要有“过程”，有几点要注意：有问必答，按要求答。高考数学试卷大题一般都有两三个小题，大多一题一个回答，但有时一个小题中需要多个回答，不能答了一个忘了其他。\n——命题意图：图，向量坐标，和向量，差向量，模(图，线段长，中点，中线长…)——向量坐标表示，向量运算，解t的方程\n例9、(2011)如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB=AD，∠BAD=60°，E，F分别是AP，AD的中点.求证：(1)直线EF∥平面PCD；(2)平面BEF⊥平面PCD.本小题主要考查直线与平面、平面与平面的位置关系，考查空间想象能力和推理论证能力。PABCDEF\n如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB=AD，∠BAD=60°，E，F分别是AP，AD的中点.求证：(1)直线EF∥平面PCD；分段：中位线→线线平行线线平行→线面平行说明：两个给分段独立给分。PABCDEF\n如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB=AD，∠BAD=60°，E，F分别是AP，AD的中点.求证：(2)平面BEF⊥平面PAD.分段：正三角形→线线垂直线线垂直→线面垂直线面垂直→面面垂直PABCDEF\n(2012)如图，在直三棱柱ABC-A1B1C1中，A1B1=A1C1，D，E分别是棱BC，CC1上的点(点D不同于点C)，且AD⊥DE，F是B1C1的中点.求证：(1)平面ADE⊥平面BCC1B1；直棱柱性质CC1⊥面ABC线面垂直性质CC1⊥AD线面垂直判定AD⊥面BCC1B1面面垂直判定面ADE⊥面BCC1B1FA1B1C1ABDCE\n等腰△判、性A1F⊥B1C1线面垂直性质CC1⊥A1F线面垂直判定A1F⊥面BCC1B1线面垂直性质AD∥A1F线面平行判定A1F∥面ADE直棱柱性质CC1⊥平面ABCFA1B1C1ABDCE求证：(2)直线A1F∥平面ADE.\n3、中档题的苦味例10、制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测，甲、乙项目可能的最大盈利率分别为100﹪和50﹪，可能的最大亏损分别为30﹪和10﹪.投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？\n解：设甲项目投资x万元，乙项目投资y万元，则盈利为f=x+0.5y万元,其中x≥0，y≥0，且可行域如图所示，过可行域中的点作斜率为-2的直线，当直线过点A时，f最大。AXoY由两个边界直线方程得点A(4,6),即当x=4，y=6时，f有最大值7，所以，最大收益为7万元。\n创新建模能把住关！Ox(km)y(km)\nOx(km)y(km)创新建模能把住关！\nOx(km)y(km)创新建模能把住关！\n应用题考查两方面的要求，实际问题与数学模型的互化、数学模型求解，解答表述时不能忽视。中学阶段学习过如下类型的应用题：函数应用题、数列应用题、三角测量应用题、线性规划应用题、排列组合应用题、统计概率应用题……，有不知如何恰当表达的，要查课本例题的解答格式，了解要求。\nOxyFBMTNA3、解几题要看真功夫——运算模块训练：交点弦长、过定点、轨迹方程、向量方法\nxyABOFTMNOxyFBMTNA\n\n例13、如图，在平面直角坐标系xOy中，M、N分别是椭圆x2/4+y2/2=1的顶点，过坐标原点的直线交椭圆于P、A两点，其中P在第一象限，过P作x轴的垂线，垂足为C，连接AC，并延长交椭圆于点B，设直线PA的斜率为k．(1)当直线PA平分线段MN，求k的值；(2)当k=2时，求点P到直线AB的距离d；(3)对任意k>0，求证：PA⊥PB．——得分差异最大的试题OxyCBMPNA\n再说运算：yxOF1F2PAB\n2012的18题、若函数y=f(x)在x=x0处取得最大值或最小值，则称x0为函数y=f(x)的极值点。已知a，b是实数，1和－1是函数f(x)=x3+ax2+bx的两个极值点。(1)求a和b的值；(2)设函数g(x)的导函数g′(x)=f(x)+2，求g(x)的极值点；(3)设h(x)=f(f(x))－c，其中c∈[－2,2]，求函数y=h(x)的零点个数。(3)数方程h(x)=(x3－3x)3－3(x3－3x)－c=0的根，令h0(x)=(x3－3x)3－3(x3－3x)，数与y=c的交点个数…函数把关：\n4、压轴题要仔细品味\n若对于任意的m∈(0,1)，总有f[mx1+(1－m)x2]≤mf(x1)+(1－m)f(x2)成立，则称f(x)为c函数……\nABPx2+m(x1-x2)x1+m(x2-x1)Q\n\n\n例17、设M为部分正整数组成的集合，数列{an}的首项a1=1，前n项的和为Sn，已知对任意整数k属于M，当n＞k时，Sn+k+Sn-k=2(Sn+Sk)都成立．(1)设M={1}，a2=2，求a5的值；(2)设M={3,4}，求数列{an}的通项公式．命题的背景:(n+k)2+(n－k)2=2n2+2k2，k可以任取。n2是数列1，3，5，7，9，…的前n项和；即Sn+k+Sn-k=2(Sn+Sk)总成立，k可以任取。若k取某一个正整数，数列定是1，3，5，7，…吗？\n例17、设M为部分正整数组成的集合，数列{an}的首项a1=1，前n项的和为Sn，已知对任意整数k属于M，当n＞k时，Sn+k+Sn-k=2(Sn+Sk)都成立．(2)设M={3,4}，求数列{an}的通项公式．怎么想？具体写出性质Sn+3+Sn-3=2(Sn+S3)，再写下一个Sn+4+Sn-2=2(Sn+1+S3)，两个相减得an+4+an-2=2an+1，n≥4，即有a2，a5，a8，a11，…成等差数列，设公差是3d1；a3，a6，a9，a12，…成等差数列，设公差是3d2；a4，a7，a10，a13，…成等差数列，设公差是3d3；\n两个相减得an+4+an-2=2an+1，n≥4，即有a2，a5，a8，a11，…成等差数列，设公差是3d1；a3，a6，a9，a12，…成等差数列，设公差是3d2；a4，a7，a10，a13，…成等差数列，设公差是3d3；当k=4时，同理有an+5+an-3=2an+1，n≥5，即有a3，a7，a11，a15，…成等差数列，设公差是4b1；a4，a8，a12，a16，…成等差数列，设公差是4b2；a5，a9，a13，a17，…成等差数列，设公差是4b3；a2，a6，a10，a14，…成等差数列，设公差是4b4；——b1=d2=b2=d3=b3=d1…？\n怎么想？具体写出性质Sn+3+Sn-3=2(Sn+S3)，再写下一个Sn+4+Sn-2=2(Sn+1+S3)，两个相减得an+4+an-2=2an+1，n≥4，注意到a2，a5，a8，a11，…成等差数列；a3，a6，a9，a12，…成等差数列；a4，a7，a10，a13，…成等差数列；设三数列公差分别是3d1，3d2，3d3，若写Sn+4+Sn-4=2(Sn+S4)与第一式作差，则an+7－an=2a4，——也是等差数列但公差定了！a1，a2怎么归队？\n5、廿三题怎一个抢字了得——半小时的加试策略、4年23题的力求创新\n例19(2010)、已知△ABC的三边长都是有理数．(1)求证：cosA是有理数；(2)对任意正整数n，求证cosnA是有理数．——有理数——cos(k+1)A=coskAcosA－sinkAsinA\n\n\n高考的“五味”1、闯小关取舍休得两依依——酸2、送分的大题请您别客气——甜3、解几应用题还看真功夫——苦4、压轴的问题需要细品味——辣5、廿三题怎一个抢字了得——辛——每个人要有自己的应考方略\n——每个人要有自己的应考方略：1、5分钟的读题时间能否形成总体了解；2、时间的几种分割；3、13、14题的取舍；4、一卷的复看检查，注意“惯性”；5、最后的半小时抢什么？\n二模后的安排原则：保温与冲刺阶段，以做为主，做中档题为主！(1)二模的反思与纠错——每人自查，反思30例解错的题(2)回归课本(立体几何定理，概率统计体系，应用题的格式规范，难题新题的课本背景、链接内容的了解)(3)创新题探究——3课15例，外加习题(4)典型试题再做——(10—2—5)(5)热身小练——6月的5个小练习回过来看后四周的安排\n(1)在基本概念和典型问题上下功夫：单调的判定与性质、圆锥曲线交点、数列通项(2)在思想方法上做功课：函数的建模、化归(3)在心态信心上花力气：学生水平能力的基本定位、保与冲的应对(4)在考试策略上作文章：学生高考分数目标的定位与考试策略\n不当之处敬请指正！