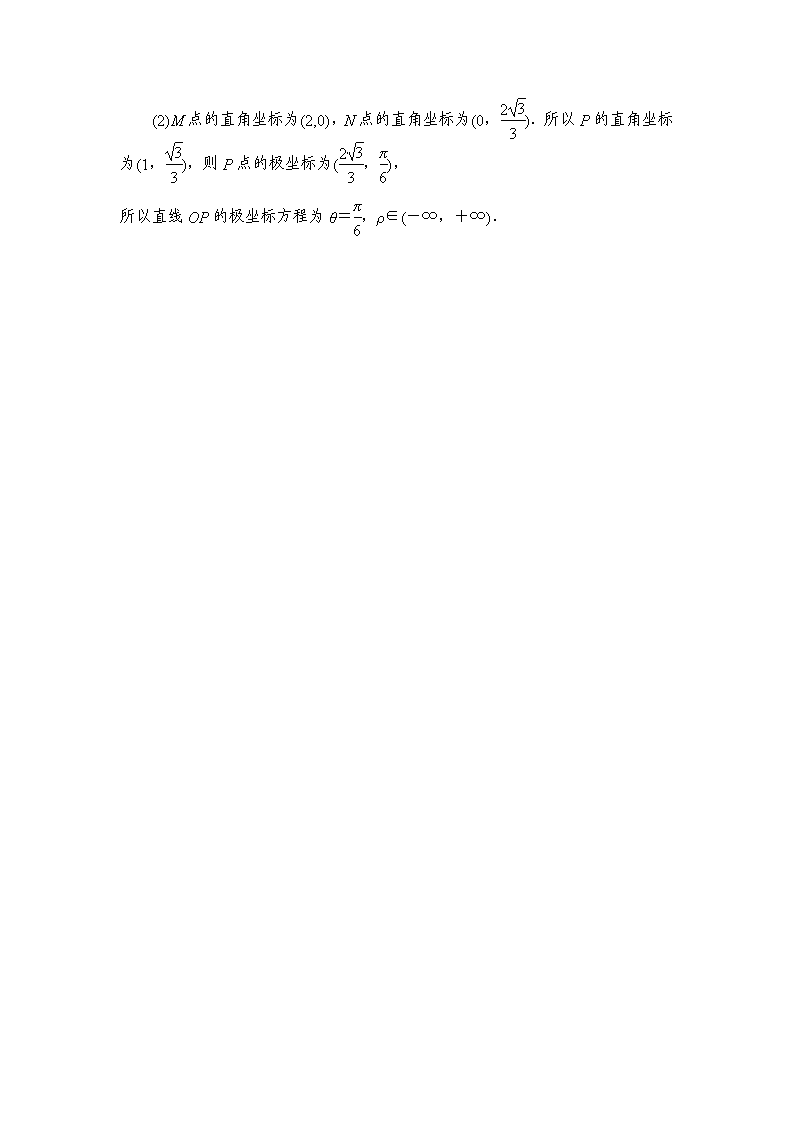- 45.50 KB
- 2022-07-22 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
课时作业(六十一)一、选择题1.在同一平面直角坐标系中,经过伸缩变换后,曲线C变为曲线x′2+y′2=1,则曲线C的方程为( )A.25x2+9y2=1 B.9x2+25y2=1C.25x+9y=1D.+=1答案 A2.设点M的直角坐标为(-1,-,3),则它的柱坐标为( )A.(2,,3)B.(2,,3)C.(2,,3)D.(2,,3)答案 C3.极坐标方程ρcosθ=2sin2θ表示的曲线为( )A.一条射线和一个圆B.两条直线C.一条直线和一个圆D.一个圆答案 C4.(·大连)极坐标方程ρ=cosθ化为直角坐标方程为( )A.(x+)2+y2=B.x2+(y+)2=C.x2+(y-)2=D.(x-)2+y2=答案 D解析 由ρ=cosθ得ρ2=ρcosθ,∴x2+y2=x.选D.二、填空题5.直线xcosα+ysinα=0的极坐标方程为________.答案 θ=α+6.在极坐标系中,点A(1,)到直线ρsinθ=-2的距离是________.答案 2+7.在极坐标系中,直线ρsin(θ+)=2被圆ρ=4截得的弦长为________.答案 4解析 直线ρsin(θ+)=2可化为x+y-2=0,圆ρ=4可化为x2+y2=16,由圆中的弦长公式得2=2=4.8.极坐标方程分别为ρ=2cosθ和ρ=sinθ的两个圆的圆心距为________.\n答案 解析 两圆方程分别为x2+y2=2x,x2+y2=y,知两圆圆心C1(1,0),C2(0,),∴|C1C2|==.9.在极坐标系中,点(1,0)到直线ρ(cosθ+sinθ)=2的距离为________.答案 解析 直线ρ(cosθ+sinθ)=2可化为x+y-2=0,故点(1,0)到直线距离d==.10.两直线ρsin(θ+)=,ρsin(θ-)=的位置关系是________.(判断垂直或平行或斜交)答案 垂直解析 两直线方程可化为x+y=,y-x=,故两直线垂直.11.在极坐标系中,若过点A(3,0)且与极轴垂直的直线交曲线ρ=4cosθ于A、B两点,则|AB|=________.答案 2解析 曲线ρ=4cosθ,即为圆x2+y2-4x=0,过A(3,0)且与极轴垂直的直线为x=3,将x=3代入x2+y2-4x=0,得y2=12-9=3,∴y=±.故|AB|=2.三、解答题12.(·江苏扬州)求以点A(2,0)为圆心,且过点B(2,)的圆的极坐标方程.解析 由已知圆的半径为AB==2,又圆的圆心坐标为A(2,0),所以圆的普通方程为(x-2)2+y2=4.由得圆的极坐标方程是ρ=4cosθ.13.(09·辽宁)在直角坐标系中xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为ρcos(θ-)=1,M,N分别为C与x轴,y轴的交点.(1)写出C的直角坐标方程,并求M,N的极坐标;(2)设MN的中点为P,求直线OP的极坐标方程.解析 (1)由ρcos(θ-)=1得ρ(cosθ+sinθ)=1.从而C的直角坐标方程为x+y=1,即x+y=2.\nθ=0时,ρ=2,所以M(2,0).θ=时,ρ=,所以N(,).(2)M点的直角坐标为(2,0),N点的直角坐标为(0,).所以P的直角坐标为(1,),则P点的极坐标为(,),所以直线OP的极坐标方程为θ=,ρ∈(-∞,+∞).