西峡五里桥初中李纳课件 18页

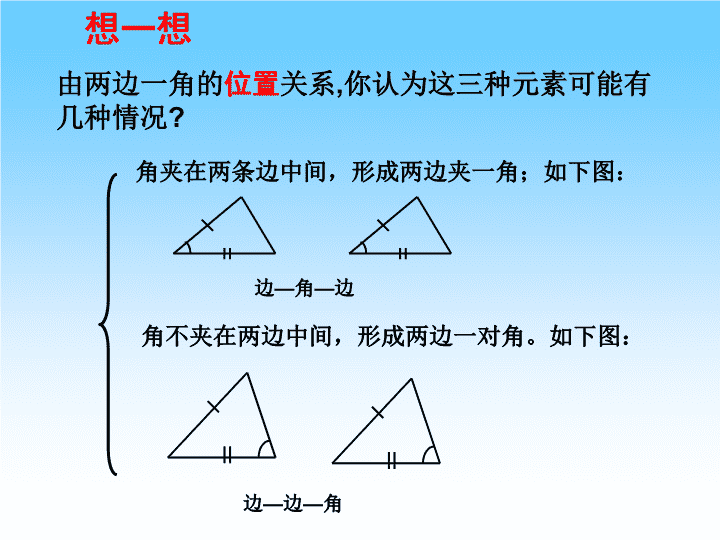
第十九章全等三角形华师大版八年级数学19.2.2边角边西峡县丹水二中胡庚芳\n思考如果两个三角形有三组对应相等的元素（边或角），那么会有哪几种可能的情况？有以下的四种情况：两边一角、两角一边、三角、三边．温馨提示要不重不漏哦\n想一想由两边一角的位置关系,你认为这三种元素可能有几种情况?角夹在两条边中间，形成两边夹一角；如下图：角不夹在两边中间，形成两边一对角。如下图：边—角—边边—边—角\n已知:两条长为6cm和8cm的两条线段以及一个角45°(1)操作:以这两条线段为边,以45°为一个角,按所给的步骤,画一个三角形.(2)比较:在同一小组内,比较所画的三角形是否全等?怎样比较?你们所画的三角形有什么共同条件?(3)思考:通过以上操作比较,你能发现什么结论?4分钟后,比谁能较好的解决以上问题步骤：1、画一线段AB，使它等于8cm；2、画∠MAB＝45°；3、在射线AM上截取AC＝6cm；4、连结BC．△ABC即为所求．自探提示\nCBAC′B′A′CBA从运动变换的角度来理解如果两个三角形有两边及其夹角分别对应相等，那么这两个三角形全等。由于AB＝A′B′，我们移动其中的△ABC，使点A与点A′、点B与点B′重合；因为∠B＝∠B′，因此可以使∠B与∠B′的另一边BC与B′C′重叠在一起，而BC＝B′C′，因此点C与点C′重合．于是△ABC与△A′B′C′重合，这就说明这两个三角形全等．三角形全等的判定公理:边角边简记为S.A.S\n用符号语言表达为：在△ABC与△A’B’C’中AB=A’B’∠B=∠B’BC=B’C’∴△ABC≌△A’B’C’（SAS）CBAC’B’A’\n如图19.2.4，在△ABC中，AB＝AC，AD平分∠BAC，求证：　△ABD≌△ACD．证明:∵AD平分∠BAC，∴　∠BAD＝∠CAD．在△ABD与△ACD中，AB＝AC，(已知)∠BAD＝∠CAD，(已证)AD＝AD，(公共边)∴△ABD≌△ACD（S.A.S.）．∵练一练\n以3cm、4cm为三角形的两边，长度3cm的边所对的角为45°，情况又怎样？动手画一画，你发现了什么？ABC3cm4cm45°3cm结论：两边及其一边所对的角相等，两个三角形不一定全等做一做问题：那么边边角对应相等时情况又是怎样的呢？MB’步骤：1.画一线段AC,使它等于4cm2.画∠CAM=45°3.以C为圆心,3cm长为半径画弧,交AM于点B4.连结CB△ABC就是所求做的三角形显然：△ABC与△AB’C不全等和B’、CB’与△AB’C\n质疑再探:你对本节的知识还有什么疑问?你还有什么新的问题吗?大胆提出来与同学们交流.\n请你运用本节知识自编1—2道习题,和同桌交流.(形式不限,可以是填空,选择,解答)运用拓展:\n1.如图所示,根据题目条件，判断下面的三角形是否全等．为什么?（1）AC＝DF，　∠C＝∠F，BC＝EF（2）BC＝BD，　∠ABC＝∠ABD．（3）AB＝AC，AE=AF（4）OA=OC，OB=OD口答ABCDO\n链接生活：1、小明不小心打翻了墨水，将自己所画的三角形涂黑了，你能帮小明想想办法，画一个与原来完全一样的三角形吗？\n2、因铺设电线的需要，要在池塘两侧A、B处各埋设一根电线杆（如图），因无法直接量出A、B两点的距离，现有一足够的米尺。请你设计一种方案，粗略测出A、B两杆之间的距离。。链接生活：\n小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结CD，用米尺测出DE的长，这个长度就等于A，B两点的距离。请你说明理由。想一想在△ACB和△DCE中∵AC=DC∠ACB=∠DCEBC=EC∴△ACB≌△DCE(S.A.S.)∴AB=DE∵\n4.点M是等腰梯形ABCD底边AB的中点，求证：△AMD≌△BMC．证明：在等腰梯形ABCD中，AB∥DCAD=BC∠A＝∠B∵点M是底边AB的中点∴AM=BM在△ADM和△BCM中AD＝BC∠A＝∠BAM＝BM∴△AMD≌△BMC(SAS)∵\n通过本节课的学习,你学到了那些知识?你还有那些收获?课堂小结\n小结：1．根据边角边公理判定两个三角形全等，要找出两边及夹角对应相等的三个条件．2．找使结论成立所需条件，要充分利用已知条件(包括给出图形中的隐含条件，如公共边、公共角等)，并要善于运用学过的定义、公理、定理．3．证明的书写格式：(1)通过证明，先把题设中的间接条件转化成为可以直接用于判定三角形全等的条件；(2)再写出在哪两个三角形中：具备按边角边的顺序写出可以直接用于判定全等的三个条件；(3)最后写出判定这两个三角形全等的结论．\n谢谢指导再见