高中物理竞赛热学模拟试题及答案 11页

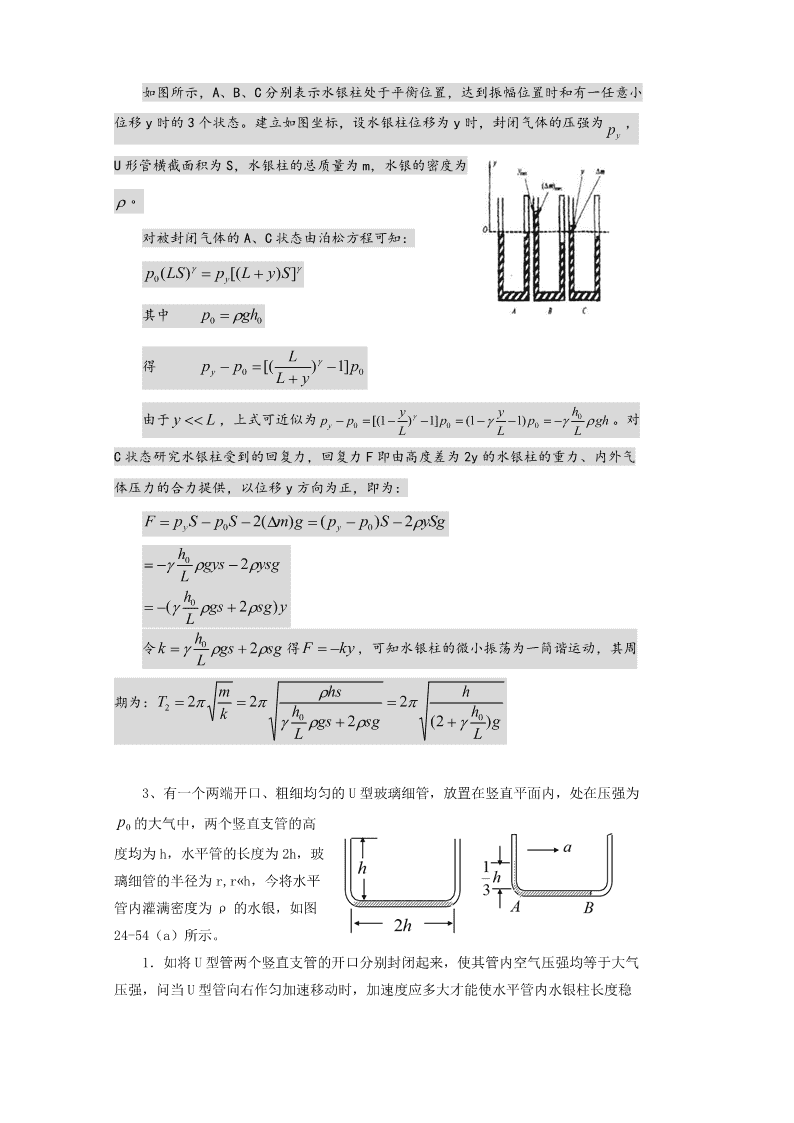
高中物理竞赛热学模拟试题及答案1、某水银气压计的玻璃管顶端高出水银槽液面1m。如图所示，因上部混入少量空气，使其读数不准。当气温为27ºC，标准气压计读数仍为76cmHg时，该气压计读数为70cmHg。（1）在相同气温下，若用该气压计测量气压，测得读数为68cmHg，则实际气压应为多少厘米汞柱？（2）若在气温为-3ºC时，用该气压计测得气压读数仍为70cmHg，则实际气压应为多少厘米汞柱？解：（1）以混入气压计内气体为研究对象，因温度不变，有p0V0P1V1，p076706(cmHg)V0(10070)S30S，V1(10068)S32S30则P165.6(cmHg)32实际气压pp16873.6(cmHg)（2）因体积不变，有p0/T0P2/T2，T027327300(K)T22733270(K)，p06cmHg则P26270/3005.4(cmHg)实际气压PP27075.4(cmHg)2、在两端开口的竖直放置的U型管中注入水银，水银柱的全长为h,若把管的右端封闭，被封闭的空气柱长L，然后使水银柱作微小的振荡，设空气为理想气体，且认为水银振荡时右管内封闭气体经历的是准静态绝热过程，大气压强相当于h0水银柱产生的压强，空气的绝热指数为。试求水银振动的周期T2。已知对于理想气体的绝热过程有PV=常数。解：右端封闭后，随着水银柱的振荡，被封闭的空气经历绝热膨胀或绝热压缩过程；封闭端的空气与外界空气对水银柱压强差提供水银柱作微小振动的回复力，本题关注回复力的构成及所循规律。\n如图所示，A、B、C分别表示水银柱处于平衡位置，达到振幅位置时和有一任意小位移y时的3个状态。建立如图坐标，设水银柱位移为y时，封闭气体的压强为，pyU形管横截面积为S，水银柱的总质量为m，水银的密度为。对被封闭气体的A、C状态由泊松方程可知：p(LS)p[(Ly)S]0y其中pgh00L得pp[()1]py00Lyyyh0由于yL，上式可近似为pp[(1)1]p(11)pgh。对y000LLLC状态研究水银柱受到的回复力，回复力F即由高度差为2y的水银柱的重力、内外气体压力的合力提供，以位移y方向为正，即为：FpSpS2(m)g(pp)S2ySgy0y0h0gys2ysgLh0(gs2sg)yLh令0gssgk2得Fky，可知水银柱的微小振荡为一简谐运动，其周Lmhsh期为：T2222kh0h0gs2sg(2)gLL3、有一个两端开口、粗细均匀的U型玻璃细管，放置在竖直平面内，处在压强为p0的大气中，两个竖直支管的高度均为h，水平管的长度为2h，玻璃细管的半径为r,r«h，今将水平管内灌满密度为ρ的水银，如图24-54（a）所示。1．如将U型管两个竖直支管的开口分别封闭起来，使其管内空气压强均等于大气压强，问当U型管向右作匀加速移动时，加速度应多大才能使水平管内水银柱长度稳\n5定为h。32．如将其中一个竖直支管的开口封闭起来，使其管内气体压强为1atm，问当U型管绕以另一个竖直支管（开口的）为轴作匀速转动时，转数n应为多大才能使水平管5内水银柱长度稳定为h。3（U型管作以上运动时，均不考虑管内水银液面的倾斜）解：1、当U型管向右加速移动时，水平管内的水银柱将向左边的竖直支管中移动，其稳定的位置是留在水平管内的水银柱所受的水平方向的合力等于使其以恒定加速度a向右运动时所需的力。由于竖直支管内空气在膨胀或压缩前后的温度相等，根据气态方程有4右管：p0hSp1hS32左管：p0hSp2hS31S为管的截面积，图中，A、B两处压强分别为：pAp2gh3pBp15而留在水平管内的水银柱质量mhS3其运动方程为(pApB)Sma由以上各式可得a(9p04gh)/(20h)2．当U型管以开口的竖直支管为轴转动时，水平管内h/3的水银柱将向封闭的竖直支管中移动，其稳定位置是水平BA管内的水银柱所受的水平方向的合力，正好等于这段水银柱作匀速圆周运动所需的向心力。由于封闭竖直支管内空2气在压缩前后的温度相等，根据气态方程有p0hShS31S为管的截面积。图中A、B两处的压强分别为pApgh3pBp05留在水平管内的水银柱的质量mhS3222其运动方程为(pp)SmR4nmRAB7其中Rh6\n1由以上各式可得22n(9p6gh)/(140h)204、在大气压下用电流加热1个绝热金属片，使其以恒定的功率P获取电热，发现在一定的温度范围内金属绝对温度T随时间t的增长关系为1/4T(t)T[1a(tt)]。其中T0、a、t0均为常量。求该金属片的热容量CP随温度T00变化的关系。Pt解：由热容量定义C，而pT11TT[1at(tt)]44T[1att()]0000tt1311T{[1att()]4[1att()]4at[1att()]}400004t3Ta04[1att()]04TaT003[]4T4P3故CTp3aT05、如图所示，截面均匀，下端A封闭的细长试管AB竖直放置，管下端A内封有长为L0的空气，管中间是长为4L0的水银柱，管上端B有长为L0的空气。管中间有长为L=4L0的水银柱管上端B有长为L0的空气。开始时，管上端B与大气连通，大气压强为p0=2ρgL，其中ρ为水银密度。（1）如果先将B端封闭，再将试管缓慢转过180°，试问管中A端空气柱长度LA与B端空气柱长度LB各为多少？（2）如果B端始终与大气连通，不封闭，先将试管缓慢倒转180°，再缓慢回转180°复原。试问最后管中A端空气柱长度L与B端空气柱长度AL各为多少L0？B设倒转过程均在大气环境下进行，温度不变。解：（1）倒转前后，对于A、B气体有pALAp0gLL0,pBLBp0L0pAgLLB而LALB2L0,p02gL,L4L0所以求得LA1.37L0,LB0.63L0.\n（2）设倒转后水银不外泄，对于A端空气柱有p0gLL0p0gLLA求得LA3L0说明水银外泄一部分。设倒转后，剩下水银柱长度为L，A端长度为LA，则有p0gLL0p0gLLA,LAL2L0L6L0，解得LA2.61L0,L3.39L0。回转过程中，有pgLLpgLLpgLL,LLL，000A0ABAA求得L1.05L,L1.55L。A0B06、如图所示，有一个直立的气缸，气缸底到气缸口的距离为L0cm，用一厚度和质量均可忽略不计的刚性活塞A，把一定质量的空气封在气缸内，活塞与气缸间的摩擦可忽略。平衡时活塞上表面与气缸口的距离很小（计算时可忽略不计），周围大气的压强为H0cmHg。现把盛有水银的一个瓶子放在活塞上（瓶子的质量可忽略），平衡时活塞到气缸底的距离为Lcm。若不是把这瓶水银放在活塞上，而是把瓶内水银缓缓不断地倒在活塞上方，这时活塞向下移，压缩气体，直到活塞不再下移，求此时活塞在气缸内可能的位置以及与之相对应的条件（即题中给出量之间应满足的关系），设气体的温度不变。解一：设整瓶水银放在活塞上后，使气缸内气体增加的压强为hcmHg；由玻意耳定律H0L0(H0h)LH(LL)00得h（1）L式中L为此时活塞所在位置与缸底距离，h的大小反映了水银质量的大小。当水银注入后，活塞不再下移时，设活塞上水银的深度为Hcm，活塞下移的距离为xcm，则由玻意耳定律H0L0(H0H)(L0x)H0解得Hx（2）Lx0可能发生两种情况：（1）水银比较少，瓶内水银全部注入后，尚未灌满或刚好灌满活塞上方的气缸，这时有Hh（3）\n而且有Hx由（1）（2）（3）式得xL0L活塞到气缸底的距离LL0xLH0Hxxlx0所以LH0若LH0，则有LL（2）瓶内水银比较多，当活塞上方的气缸灌满水银时，瓶内还剩有一定量的水银，这时Hx（4）Hh（5）由（2）（4）式得xL0H0则活塞到气缸底的距离LL0xH0由（1）（4）（5）式得LH0可见，若LH0，则LH0解二：设整瓶水银放在活塞上后，使气缸内气体增加的压强为hcmHg，由玻意耳定律得H0L0(H0h)LH(LL)00hL这也是全部水银倒在活塞上而无溢出时水银柱的高度。当将水银缓缓倒向活塞直到活塞不再下移时，对应着水银能全部倒在活塞上而无溢出和只有部分水银倒在了活塞上水银就开始溢出两种可能情况。下面对这两种情况分别讨论：H(LL)h(LL)00LLLH（1）当0，即0时，得0，瓶中水银可全部倒L入而无溢出。此种情况与将整瓶水银放在活塞上等效，故活塞到缸底的距离L=L。H(LL)（2）当h(LL)，即00LL，得LH，瓶中水银只有部分倒在000L活塞上就开始溢出。设此时活塞到缸底的距离为L，由玻意耳定律有H0L0(H0L0L)L即此时水银高度只有(L0L)，此时压强为p0(L0L)LH求得0由此可以得出：当LH0时，LL；当LH0时，LH0\n高中物理竞赛热学模拟试题答案1、解：（1）以混入气压计内气体为研究对象，因温度不变，有p0V0P1V1，p076706(cmHg)V0(10070)S30S，V1(10068)S32S30则P165.6(cmHg)32实际气压pp16873.6(cmHg)（2）因体积不变，有p0/T0P2/T2，T027327300(K)T22733270(K)，p06cmHg则P26270/3005.4(cmHg)实际气压PP27075.4(cmHg)2、解：右端封闭后，随着水银柱的振荡，被封闭的空气经历绝热膨胀或绝热压缩过程；封闭端的空气与外界空气对水银柱压强差提供水银柱作微小振动的回复力，本题关注回复力的构成及所循规律。如图所示，A、B、C分别表示水银柱处于平衡位置，达到振幅位置时和有一任意小位移y时的3个状态。建立如图坐标，设水银柱位移为y时，封闭气体的压强为，pyU形管横截面积为S，水银柱的总质量为m，水银的密度为。对被封闭气体的A、C状态由泊松方程可知：p(LS)p[(Ly)S]0y其中pgh00L得pp[()1]py00Lyyyh0由于yL，上式可近似为pp[(1)1]p(11)pgh。对y000LLLC状态研究水银柱受到的回复力，回复力F即由高度差为2y的水银柱的重力、内外气\n体压力的合力提供，以位移y方向为正，即为：FpSpS2(m)g(pp)S2ySgy0y0h0gys2ysgLh0(gs2sg)yLh令0gssgk2得Fky，可知水银柱的微小振荡为一简谐运动，其周Lmhsh期为：T2222kh0h0gs2sg(2)gLL3、解：1、当U型管向右加速移动时，水平管内的水银柱将向左边的竖直支管中移动，其稳定的位置是留在水平管内的水银柱所受的水平方向的合力等于使其以恒定加速度a向右运动时所需的力。由于竖直支管内空气在膨胀或压缩前后的温度相等，根据气态方程有4右管：p0hSp1hS32左管：p0hSp2hS31S为管的截面积，图中，A、B两处压强分别为：pAp2gh3pBp15而留在水平管内的水银柱质量mhS3其运动方程为(pApB)Sma由以上各式可得a(9p04gh)/(20h)2．当U型管以开口的竖直支管为轴转动时，水平管内h/3的水银柱将向封闭的竖直支管中移动，其稳定位置是水平BA管内的水银柱所受的水平方向的合力，正好等于这段水银柱作匀速圆周运动所需的向心力。由于封闭竖直支管内空气在压缩前后的温度相等，根据气态方程有B1S为管的截面积。图中A、B两处的压强分别为pApgh3pBp0\n5留在水平管内的水银柱的质量mhS3其运动方程为7其中Rh61由以上各式可得22n(9p6gh)/(140h)20Pt4、解：由热容量定义C，而pT11TT[1at(tt)]44T[1att()]0000tt1311T{[1att()]4[1att()]4at[1att()]}400004t3Ta04[1att()]04TaT003[]4T4P3故CTp3aT05、解：（1）倒转前后，对于A、B气体有pALAp0gLL0,pBLBp0L0pAgLLB而LALB2L0,p02gL,L4L0所以求得LA1.37L0,LB0.63L0.（2）设倒转后水银不外泄，对于A端空气柱有p0gLL0p0gLLA求得LA3L0说明水银外泄一部分。设倒转后，剩下水银柱长度为L，A端长度为LA，则有p0gLL0p0gLLA,LAL2L0L6L0，解得LA2.61L0,L3.39L0。回转过程中，有pgLLpgLLpgLL,LLL，000A0ABAA\n求得L1.05L,L1.55L。A0B06、解一：设整瓶水银放在活塞上后，使气缸内气体增加的压强为hcmHg；由玻意耳定律H0L0(H0h)LH(LL)00得h（1）L式中L为此时活塞所在位置与缸底距离，h的大小反映了水银质量的大小。当水银注入后，活塞不再下移时，设活塞上水银的深度为Hcm，活塞下移的距离为xcm，则由玻意耳定律H0L0(H0H)(L0x)H0解得Hx（2）Lx0可能发生两种情况：（1）水银比较少，瓶内水银全部注入后，尚未灌满或刚好灌满活塞上方的气缸，这时有Hh（3）而且有Hx由（1）（2）（3）式得xL0L活塞到气缸底的距离LL0xLH0Hxxlx0所以LH0若LH0，则有LL（2）瓶内水银比较多，当活塞上方的气缸灌满水银时，瓶内还剩有一定量的水银，这时Hx（4）Hh（5）由（2）（4）式得xL0H0则活塞到气缸底的距离LL0xH0由（1）（4）（5）式得LH0可见，若LH0，则LH0解二：设整瓶水银放在活塞上后，使气缸内气体增加的压强为hcmHg，由玻意耳定律得H0L0(H0h)LH(LL)00hL这也是全部水银倒在活塞上而无溢出时水银柱的高度。当将水银缓缓倒向活塞直到活塞不再下移时，对应着水银能全部倒在活塞上而无\n溢出和只有部分水银倒在了活塞上水银就开始溢出两种可能情况。下面对这两种情况分别讨论：H(LL)h(LL)00LLLH（1）当0，即0时，得0，瓶中水银可全部倒L入而无溢出。此种情况与将整瓶水银放在活塞上等效，故活塞到缸底的距离L=L。H(LL)（2）当h(LL)，即00LL，得LH，瓶中水银只有部分倒在000L活塞上就开始溢出。设此时活塞到缸底的距离为L，由玻意耳定律有H0L0(H0L0L)L即此时水银高度只有(L0L)，此时压强为p0(L0L)求得LH0由此可以得出：当LH0时，LL；当LH0时，LH0