- 1001.50 KB
- 2022-07-25 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
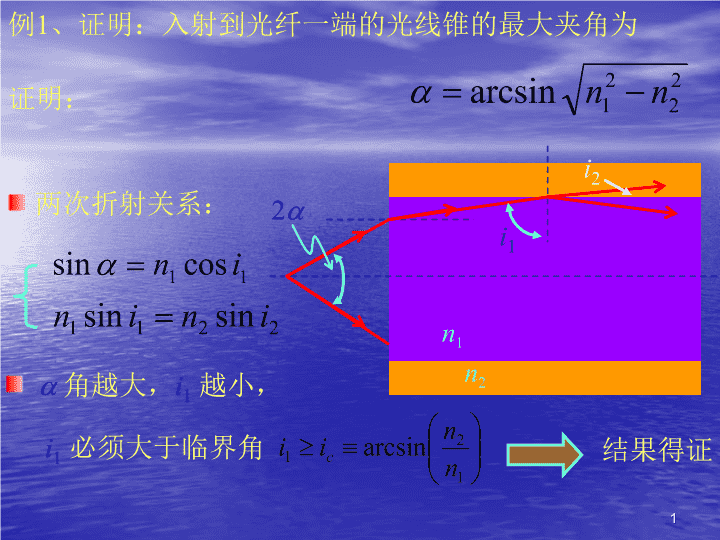
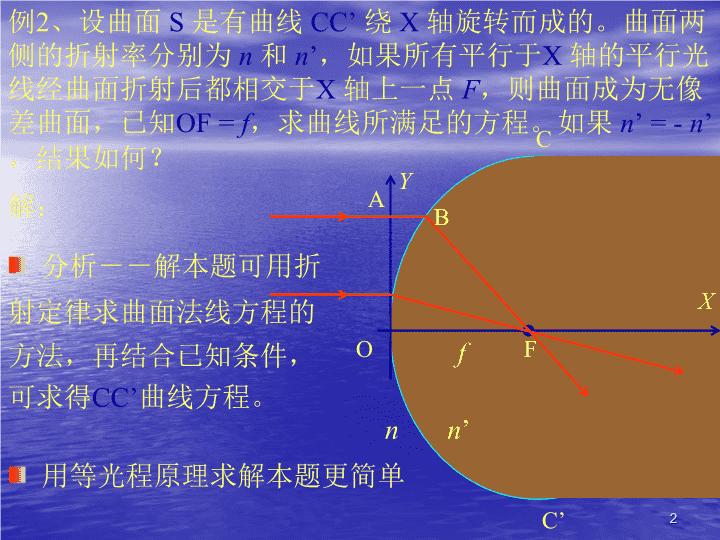
例1、证明:入射到光纤一端的光线锥的最大夹角为2an1n2证明:i1i2两次折射关系:a角越大,i1越小,i1必须大于临界角结果得证1\n例2、设曲面S是有曲线CC’绕X轴旋转而成的。曲面两侧的折射率分别为n和n’,如果所有平行于X轴的平行光线经曲面折射后都相交于X轴上一点F,则曲面成为无像差曲面,已知OF=f,求曲线所满足的方程。如果n’=-n’,结果如何?C’COXY解:FfAB分析--解本题可用折射定律求曲面法线方程的方法,再结合已知条件,可求得CC’曲线方程。用等光程原理求解本题更简单nn’2\nC’COXYFfAB(x,y)选取一条入射光线AB和一条沿X轴入射的光线;nn’等光程:几何关系:CC’曲线方程:n’=-n’时:椭圆方程抛物型反射镜3\n例1有一半导体发光管,发光区为半径为r的圆盘,发光面上覆盖一折射率为n、半径为R的半球型介质,如图所示。问:要使发光区发出的全部光线在球面上不发生全反射,介质半球的半径R至少应多大?(第11届全国中学生物理竞赛题)R发光区Onr解:第一步:全反射条件4\nOAPB第二步:反射光的几何性质考察任意一点A发出的光线在球面上任意一点P反射后的光线因此反射光线一定在APO平面内,与发光面交点B在AO延长线上,即AO所在的直径上P’RB’RP点的法线沿PO方向反射线、折射线、法线三者共面A点发出的其它光线反射后都与AO所在的直径相交5\n第二步:数学推导EFROnrPEO区内E点光线的入射角iE最大,同样FO区内F点的光线的入射角iF最大;iEiF求F点光线的最大入射角不发生全反射:如果P点在右半边,则有iF>iE,P点在左边,则反之;6\n例2图示一个盛有折射率为n的一体的槽,槽中的中部扣着一个对称屋脊形的薄璧透明罩ADB,顶角为2q,罩内为空气,整个罩子浸没在液体中,槽底AB的中点有一亮点C。试求出:位于液体上方图示平面内的眼睛从侧面观察可看到亮点的条件(液槽有足够的宽度;罩璧极薄,可不计它对光线产生折射的影响)(第13届全国中学生物理竞赛予赛题)解:ABDn’=1nCq在液面上折射时,所有光线都发生全反射时,则光线出不来。7\nABDn’=1nCqabg全反射条件:EF三角几何关系E点和F点法线的夹角=DB和水平方向的夹角:只要g的最小值小于临界角,则总会有光线出来g最小b最大C点发出光线CD的a最大8\n例3:一块平行平板,其厚度为d,光线从O点垂直入射,若平板折射率按变化,q为常数,并在A点以a角出射,求光线轨迹、A点的位置和平板的厚度。AaOXYd解:折射定律决定光线在每一点的方向,从而确定光线的轨迹;介质折射率连续变化,可将平板沿X方向切成一系列薄片,对每层薄片应用折射定律。折射定律的级联形式:bx9\nAaOXYdbxP(x,y)P点光线的方向由bx决定:P点光线的切线斜率kp:曲线y=f(x)与斜率kp:A点的条件:和光线轨迹方程:结论:和10\n例4、一个透明光学材料,折射率在y方向向两侧对称地降低:,在xoy平面内有一光线以入射角qo=30o射向O点,求此光线能到达离X轴最远的距离。OXY解:q0从上题可知,光线进入折射率非均匀介质后弯曲,而且是倾向于向折射率大的方向偏折。从图可知:光线X轴最远点为切线在水平方向时的切点处。沿Y方向分割成一系列薄层,应用折射定律。由初始条件求出a0:aa011\n例5、图示三棱镜的顶角a=60o,在三棱镜两侧对称位置放置焦距均为f=30cm的两个完全相同的凸透镜L1和L2,若在L1的前焦面上距主光轴下方y=14.3cm处放一单色点光源S,已知其像S’与S对该光学系统时左右对称的,试求该三棱镜的折射率。(第19届全国中学生物理预赛题)FfySS’L1L2解:分析:光路系统及物像左右对称,考虑到光线的可逆性原理,因此在棱镜内部分的光线一定是平行于棱镜底边an=?12\nFfySS’L1L2选取一条特征光线--通过透镜光心的光线i1i4i3i2a几何关系:bn=?计算得:13\n例7、两透镜组合系统如图,已知一个物经整个系统成像位置和大小如图中所示。试用作图法求物经L1成像位置与大小,作出L1及透镜组合系统的焦点位置(画出物方或像方中的一个即可),说明L1和L2的凹凸性。L1L2解:物P像P’物点P发出的光线1通过L1光心;通过像点P’并经过L2光心的光线2’;12’光线1经过L2后的光线1’的延长线通过像点P’;1’2在L2上对应于2’的入射光线为2;1和2交点是物点P经L1所成的中间像点;P”14\nL1L2物像12’1’2物点P发出的水平光线经L1后与P”相交确定L1的焦点F1’F’313’F’出射光线3’通过P’与光轴相交于F’L1为负透镜,L2为正透镜15\n例8、有一半径为R=0.128m的玻璃半球,过球心O并与其平面部分相垂直的直线为其主轴,在主轴上沿主轴方向放置一细条形发光体A1A2(如图示),其长度为l=0.020m。若人眼在主轴附近对着平面部分向半球望去,可以看到条形发光体的两个不很亮的像(此外可能还有亮度更暗的像不必考虑),当条形发光体在主轴上前后移动时,这两个像也在主轴上跟着移动。现在调整条形发光体的位置,使得它的两个像恰好头尾相接,连在一起,此时条形发光体的近端A2距球心O的距离为a2=0.020m,试利用以上数据求出此玻璃球的折射率n(计算时只考虑近轴光线)。OA1A2a2解:分析--两个像一为平面反射的像;另一个为经过平面折射球面反射平面折射nR16\nOA1A2a2求光轴上一点A(在O左方a处)的A经过三次所成的像,R注意点:半球的r=-Rn计算可得,最后的像A’在O右边s’A处:显然s’As’A2A’1A’2A”2A”1A经平面反射的像A”在O右边a处,两条形像头尾相接,A1’与A2”重合l17\n例9、一块玻璃台板厚度为d,折射率为n,看到压在台板下的报纸上的字相对于真实位置要上移一个距离l,试求l。SS’ndlO1O2解:S”S相对于O1的物距为s其像S”相对于O1的像距例如n=1.5,l=d/3分析--利用公式求解两次成像过程中间像S”相对于O2的物距为S’相对于O2的像距:S’相对于O1的像距:18\n例10、长度为h=4mm的物体由图示的光学系统成像。光学系统由一个直角棱镜、一个会聚透镜和一个发散透镜组成,各有关参数和几何尺寸均标于图中。求:1)像的位置;2)像的大小,并作图说明是实像还是虚像,是正立还是倒立的。(第13届全国物理竞赛复赛题)AB6cm10cm5cmL1L245o6cmn=1.5f1=20cmf2=10cm解:分析--棱镜不仅起反射作用,两个直角面上的折射也必须考虑;AB经过棱境全反射后,再分别经L1和L2成像;棱镜反射相当于反射镜,两次折射等效于平板玻璃的作用。19\n6cmA’B’平板折射像A’B’AB6cm10cm5cmL1L245o6cmn=1.5f1=20cmf2=10cm全反射条件:近轴成像棱镜的等效成像:A’B’与AB等高,在AB右侧lAB反射像6cm最后的像成在L2的焦点上,即L2左侧10cm处,像高2mm20\nA’B’L1L2作图F1F’2A”B”21\n例11、在图示的费涅尔双棱镜实验中,已知狭缝光源S的波长为l、棱镜折射率为n、棱角a很小,设光源S到棱镜的距离为L1,(1)求距棱镜L1处的屏上条纹的间距。(2)若用折射率为n’的肥皂膜遮住棱镜的一半,发现条纹上下移动了a,求肥皂膜的厚度。SS2S1解:SS2S1L1L2屏an分析--采用等效的虚光源后,有类似于扬氏干涉的干涉条纹;DxX22\nt(2)肥皂膜厚度t:求等效光源S1和S2的间距d:SS2S1L1L2屏anOd棱镜角a很小q偏向角X(1)条纹间距Dx:Dxa光程差的变化23\n例12、一块玻璃平板放置在边长为2cm的玻璃立方体上,两者之间有一层平行的空气隙。波长在0.4mm到1.15um之间的电磁波初值垂直入射到平板上,经空气隙两边表面反射而发生干涉。在此波段只有两种波长获得极大增强,其一是l1=0.4mm。求空气隙的厚度。(第3届国际奥林匹克题)解:下表面反射的光要比上表面反射的光多走2d的光程d在玻璃表面反射时,有180o的相位改变(半波损失)干涉增强条件:和可筛选出k1和k2的可能值:k1=2和k2=1l2=0.667mm24\n例13、沿着肥皂膜法线成45o角的方向观察时,膜显绿色(l1=500nm)。设肥皂膜折射率为1.33,求:(1)肥皂膜的最薄厚度。(2)如改为垂直观察,膜是何种颜色?解:dn=1.33i=45oq(1)干涉极大条件膜最薄(2)垂直入射:i=0o,q=0o可见光范围k只能取025\n例14、两平板玻璃间构成劈形空气膜,波长为500nm的单色光正入射时,观测到膜上的干涉条纹间距为1mm,求劈角a。a解:分析--XDx光程差主要决定于厚度,形成等厚条纹;正入射时,q≈0,光程差光程差改变一个波长,条纹变化一个周期26\n??条纹条纹图示:平板平整度的检测条纹亮条纹位置例14的讨论:27\n例15、一个由暗盒组成的针孔照相机,其小孔直径小孔直径为d,暗盒中像成在小孔厚距离为D的感光胶片上,物体位于小孔前L处,所用照明波长为l。(1)估计成像清清晰时小孔半径的大小;(提示:函数,对于x>0,时,y最小)(2)若使用(1)中算出的小孔,试问物体上两点间的最小距离多少时,两点的像是可分辨的?针孔成像AdDL解:分析--28\n分析--小孔成像利用光的直线传播小孔越小越好;AdDLa’几何投影像的直径小孔衍射使得像点成为像斑小孔越小越好;a”/2衍射效应增加的直径A的像的总直径a=a’+a”29\n(1)像最清晰时的小孔直径:aAdDL时,最小(2)可分辨的两物点最小间距bABbA’B’瑞利判据30\n例16、可见光垂直入射到一个每毫米有250条狭缝的衍射光栅上,在衍射角30o处会出现什么波长的光?解:q0级+1级+2级-2级-1级利用光栅方程其中:d=(1/250)毫米,q=30o31