高中物理竞赛——磁场 36页

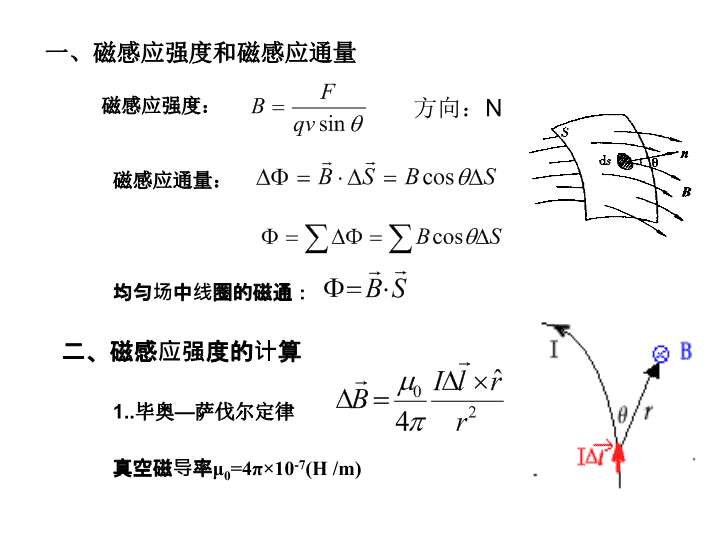
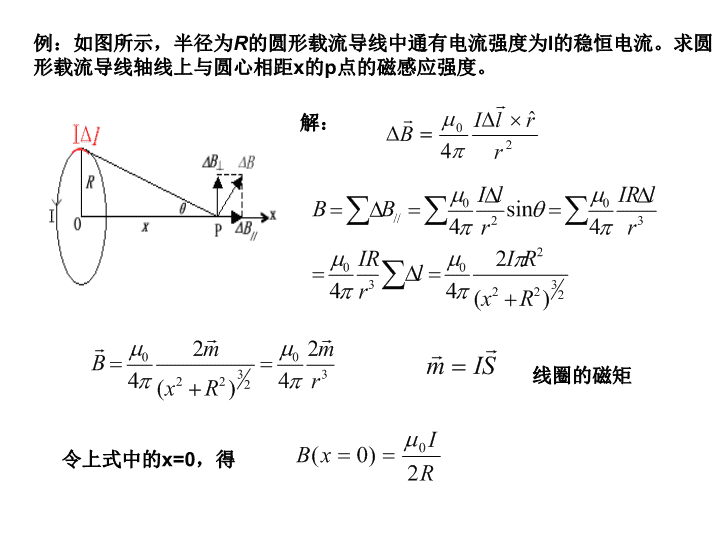
一、磁感应强度和磁感应通量二、磁感应强度的计算三、安培力载流导体受安培力运动四、洛仑兹力电荷受电磁场力的运动五、霍耳效应磁场\n一、磁感应强度和磁感应通量磁感应强度：方向：N磁感应通量：二、磁感应强度的计算1..毕奥—萨伐尔定律均匀场中线圈的磁通：真空磁导率μ0=4π×10-7(H/m)\n例：如图所示，半径为R的圆形载流导线中通有电流强度为I的稳恒电流。求圆形载流导线轴线上与圆心相距x的p点的磁感应强度。解：令上式中的x=0，得线圈的磁矩\n例：电流强度I的直线电流外的磁感应强度。B的方向如图所示，B的大小为解：取图示电流元，由毕奥—萨伐尔定律得则注：\n2.安培环路定律：几种典型电流分布的磁感应强度公式★无限长直线电流I的磁感应强度★无限长载流圆柱体的磁感应强度\n\n★细长密绕通电螺线管内轴线上的磁感应强度式中n是螺线管单位长度上线圈的匝数.密绕通电螺绕环内的磁感应强度式中n是螺线管单位长度上线圈的匝数.电流面密度为JS的无限大均匀载流平面的磁感应强度\n三、安培力载流导体受安培力运动安培力公式：载流导体受安培力运动取Δl2例载流线圈在磁场中安培力：（均匀场中）（非均匀场中）\n均匀场中曲线电流受的力等于连接曲线两端的直线电流受的力+例例\n非均匀场中载流线圈受力与运动例\n\n例：求线框(b>a)所受力和力矩、线框平衡时的θ的值，并判定平衡的稳定性。解：\n合力大小为\n合力方向(f与OI1的夹角Ψ)：求力矩：\n\n对左环电路ADCFA有关系故有因回路ADCEA所围的面积为故对该回路有解得例因\n方向向右左环所受的合力大小为同理，可求出右环所受的合力大小和方向。故\n四、洛仑兹力电荷受电磁场力的运动洛仑兹力：电荷受电磁场力运动的运动方程：\n例：电子的速率由加速电压U0决定\n设，则例解\n当即时T取最小值要摆线不松弛，必须保证，即要求\n如图示，光滑水平面上有一长为的空心细管，在管内端有一质量为，电量为的带电小球，在管的端外侧则有一不带电的小球。开始时，管静止，管带着以垂直于管长度方向的速度在平面内向右运动，小球则以速度左运动。整个装置放在垂直于水平面向下的均匀磁场．如果小球从管的端离开后，最终能与相碰，试求满足此要求的的可能取值。（内壁光滑中，其磁感应强度为例相对向在管中运动对管的压力忽略不计。）解因，小球受指向N端的洛伦兹力：其沿MN方向的加速度为：\n到达N端时，其沿MN方向的速度和所需时间分别为小球到达N端的合速度为：\n离开管N端所受洛伦兹力合其作圆周运动，回旋半径和周期分别为和在图示圆轨道上相遇，故转过的圆心角和所需时间分别为两小球相遇时运动的时间和经过的路程分别为为\n\n例如图所示，长方形磁极的长度L远大于两极间距。除边缘外，两极间的磁场是均匀磁场，磁感应强度为B0，边缘部分磁感应线弯曲(如图)。取如图所示o-xyz坐标系。电量为q(>0)的带电粒子从x=x0处以平行于z轴的初始动量p0(p0>>qB0L)从磁极左侧射入场区。试求：粒子通过场区后，在YZ平面上的小偏转角θy；试证明粒子通过场区后，在XZ平面上的小偏转角近似为（3）在X轴上取一段直线初始动量均为P0）从此段直线上各点出发射向场区。忽略粒子间的相互作用。试证明这些粒子将会聚在Z轴的某点处，该点与磁极右侧面的间距称为焦距f，试导出f的表达式。，设有一束粒子（电量均为q、；\n解（1）设粒子的质量为m，初速度为v0，则因为故粒子的动量在磁场中变化很小，偏转很小，粒子在磁场中的运动可视为速率为v0的园弧运动，圆半径为不计边缘效应，则即很小，故近似有\n（2）粒子到达磁极右侧面时，y正方向的速度分量为因磁场弯曲，边缘磁场有分量，则粒子受X方向的洛伦兹力，，为负；为负时，为正。洛伦兹力的大小为:粒子在X方向的加速度为:粒子在dt时间内，在X方向的分速度增量为:粒子在Z方向的位移是:为正时代入\n设磁极右侧面的Z坐标为Z0，则为计算这一积分，取一足够长的矩形回路L（abcda)，则由环路定律得求得\n（3）由上式知：，则，粒子向下偏转；，则，粒子向上偏转，粒子会聚。粒子会聚点与电极右侧面的距离为即焦路，所以\n例:如图1所示，分布在全空间均匀电场E的方向与+y轴平行，分布在0≤y≤L区间的均匀磁场B的方向与+Z轴平行。今有一质量为m，电量为q(q>0)的质点在x=0、y=-h、z=0的p点静止释放。设h≥0。（1）为使带电质点的运动规道恰好与y=L的平面相切，求h应满足的条件。（2）若h=0，且带电粒子的运动不走出磁场区，试写出质点x、y分量的运动方程。图1解：（1）求质点到达o点的速度（沿+y方向）\n设粒子在电场、磁场区任一点的速度分量为则即在坐标原点o：则在y=L点o：两式联列得：\n（2）质点在电磁场区作变速率曲线运动。在o点处给质点加两个大小相等图2方向相反（x方向和负x方向）的速度v（见图2），不影响粒子的运动。选择v，使则粒子在x方向作匀速直线运动。负x方向的v使质受洛伦兹力作圆周运动（图2），则由得\n(1)(2)(3)解例\n在图平而内\n五、霍耳效应如图所示，一厚为d，宽为b的载流导体薄板放在磁场B中，如果磁场与薄板板面垂直，则板的两侧A、A’间会出现电势差，这一现象叫霍耳效．A、A’间的电势差叫霍耳电势差（或霍耳电压）．若导体板中电子的浓度为n，电流为I，则霍耳电势差为:式中叫霍耳系数。