高中-物理竞赛(运动学) 13页

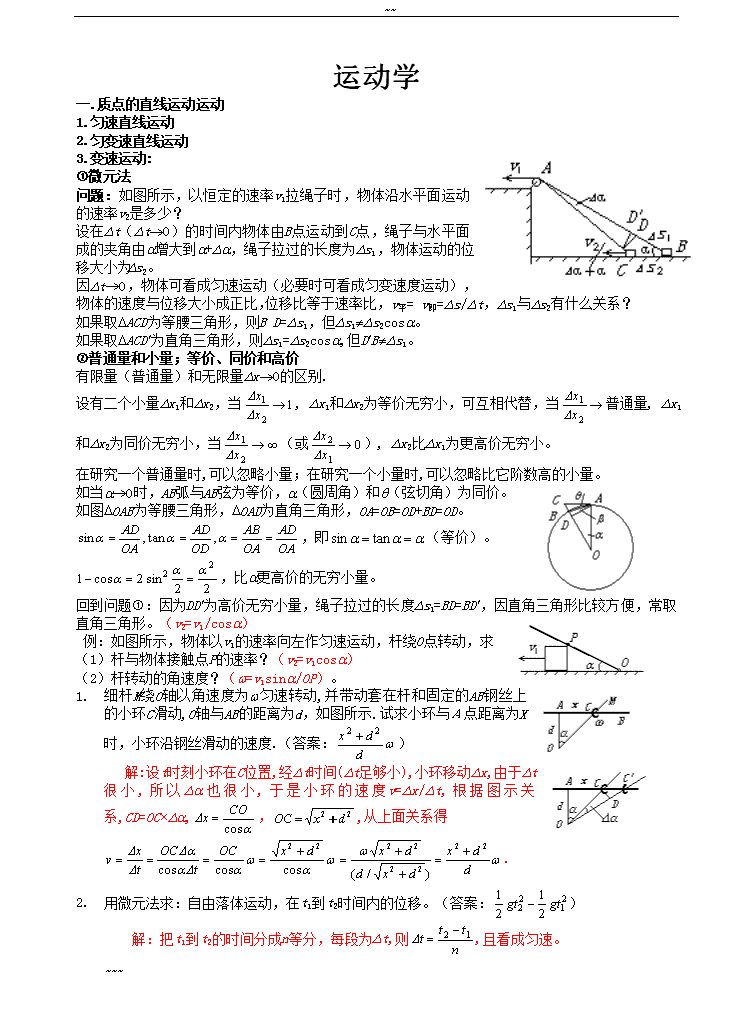
~~运动学一.质点的直线运动运动1.匀速直线运动2.匀变速直线运动3.变速运动:微元法问题：如图所示，以恒定的速率v1拉绳子时，物体沿水平面运动的速率v2是多少？设在Dt（Dt®0）的时间内物体由B点运动到C点，绳子与水平面成的夹角由a增大到a+Da，绳子拉过的长度为Ds1，物体运动的位移大小为Ds2。因Dt®0，物体可看成匀速运动（必要时可看成匀变速度运动），物体的速度与位移大小成正比，位移比等于速率比，v平=v即=Ds/Dt，Ds1与Ds2有什么关系？如果取DACD为等腰三角形，则BD=Ds1，但Ds1¹Ds2cosa。如果取DACD¢为直角三角形，则Ds1=Ds2cosa,但D¢B¹Ds1。普通量和小量；等价、同价和高价有限量（普通量）和无限量Dx®0的区别.设有二个小量Dx1和Dx2，当,Dx1和Dx2为等价无穷小，可互相代替，当普通量,Dx1和Dx2为同价无穷小，当（或）,Dx2比Dx1为更高价无穷小。在研究一个普通量时,可以忽略小量；在研究一个小量时,可以忽略比它阶数高的小量。如当a®0时，AB弧与AB弦为等价，a（圆周角）和q（弦切角）为同价。如图DOAB为等腰三角形，DOAD为直角三角形，OA=OB=OD+BD=OD。，即（等价）。，比a更高价的无穷小量。回到问题：因为DD¢为高价无穷小量，绳子拉过的长度Ds1=BD=BD¢，因直角三角形比较方便，常取直角三角形。（v2=v1/cosa）例：如图所示，物体以v1的速率向左作匀速运动，杆绕O点转动，求（1）杆与物体接触点P的速率？（v2=v1cosa）（2）杆转动的角速度？（w=v1sina/OP）。1.细杆M绕O轴以角速度为w匀速转动,并带动套在杆和固定的AB钢丝上的小环C滑动,O轴与AB的距离为d，如图所示.试求小环与Ａ点距离为X时，小环沿钢丝滑动的速度.（答案：）解:设t时刻小环在C位置,经Dt时间(Dt足够小),小环移动Dx,由于Dt很小,所以Da也很小,于是小环的速度v=Dx/Dt,根据图示关系,CD=OC´Da,，,从上面关系得.2.用微元法求：自由落体运动，在t1到t2时间内的位移。（答案：）解：把t1到t2的时间分成n等分，每段为Dt,则,且看成匀速。~~~\n~~则v1=gt1+gDt,Ds1=(gt1+gDt)Dt,v2=gt1+2gDt,Ds2=(gt1+2gDt)Dt,×××××××××vn=gt1+ngDt,Dsn=(gt1+ngDt)Dt,s=Ds1+Ds2×××××××+Dsn=.若v1=gt1,Ds1=gt1Dt,v2=gt1+gDt,Ds2=(gt1+gDt)Dt,×××××××××vn=gt1+（n-1）gDt,Dsn=[gt1+（n-1）gDt]Dt,s=Ds1+Ds2×××××××+Dsn=也可用图象法求解。1.蚂蚁离开巢沿直线爬行,它的速度与到蚁巢中心的距离成反比,当蚂蚁爬到距巢中心L1=1m的A点处时,速度是v1=2cm/s.试问蚂蚁从A点爬到距巢中心L2=2m的B点所需的时间为多少?（答案：75s）解法1:将蚁巢中心定为坐标原点O,OA连线即为x轴正方向,则坐标x处蚂蚁的速度可表示为.将AB连线分成n等份,每等份.当n很大时,每小段的运动可看成是匀速运动.每小段对应的速度为，，××××××。s解法2：各种图象的意义？因蚂蚁在任一位置时的速度,即，1/v-x的图象如图所示。蚂蚁运动的时间t为如图梯形的面积，t==75s.二.运动的合成与分解1.相对运动2.某汽艇以恒定的速率沿着河逆流航行,在某一地点丢失一个救生圈,经过t时间才发现丢失,汽艇立即调头航行,并在丢失点下游s距离处追上救生圈,则水流的速度大小为.（答案：s/2t）以地为参照物,水速为v1,船速为v2,船调头后追上救生圈的时间为t¢,对船(v2+v1)t¢=(v2-v1)+v1(t¢+t)t，得t¢=t,所以v1=s/2t.或以水为参照物,则救生圈静止,t¢=t,所以v1=s/2t3.在空间某点,向三维空间的各个方向以大小相同的速度v0射出很多的小球,问(1)这些小球在空间下落时会不会相碰?(2)经t时间这些小球中离得最远的二个小球间的距离是多少?（答案：不会相碰；2v0t）解(1)选取在小球射出的同时开始点作自由下落作参照系,则小球都以v0的速度作匀速直线运动,小球始终在以抛出点为圆心的球面上,所以小球不会相碰.(2)这些小球中离得最远的二个小球间的距离等于球面的直径,即d=2v0t.4.一只气球以10m/s的速度匀速上升,某时刻在气球正下方距气球为10m的地方有一个石子以v0的初速度竖直上抛(取g=10m/s2),石子要击中气球,则v0应满足什么条件?~~~\n~~（答案：m/s）解法1:设气球的速度为v,开始相距为h,当石子与气球的速度相等时追上,石子要击中气球,否则石子不能击中气球,速度相等时所用的时间t=(v0-v)/a---(1),则好击中时的位移关系为v0t-gt22=vt+h---(2)解得石子的初速度至少m/s.解法2:以气球为参照物,则初速度v1=v0-v,未速度v2=0,所以(v0-v)2=2gh,解得石子的初速度至少m/s.2.物体系的相关速度：杆、绳上各点在同一时刻具有相同的沿杆、绳的分速度（即两质点间的距离的改变只取决于沿它们连线方向分运动，而它们相对方们位改变只取决于垂直连线方向的分运动）。求下列各图中v1和v2的关系.答案依次是：A:v1=v2cosa;B:v1=v2cosa;C:v1cosq=v2cosa;D:v2=vtana;1.如图所示，AB杆的A端以匀速v沿水平地面向右运动，在运动时杆恒与一半圆周相切，半圆周的半径为R，当杆与水平线的交角为q时，求此时：（1）杆上与半圆周相切点C的速度大小。（2）杆转动的角速度。（3）杆上AC中点的速度大小。（4）杆与半圆周相切的切点的速度大小。[答案：（1）；（2）；（3）；；（4）]解：把A的速度分解成沿杆的速度，和垂直杆方向速度。（1）沿同一杆的速度相等，所以杆上与半圆周相切点C的速度大小。（2）A点对C点的转动速度为，所以杆转动的角速度为。（3）（4）在相同时间内，杆转过的角度与切点转过的角度相同，所以切点转动的角速度也为，杆与半圆周相切的切点的速度大小。2.如图所示，杆长为，可绕过点的水平轴在竖直平面内转动，其端点系着一跨过定滑轮、的不可伸长的轻绳，绳的另一端系一物块，滑轮的半径可忽略，在的正上方，之间的距离为。某一时刻，当绳的段与之间的夹角为时，杆的角速度为，求此时物块的速率。解：，沿绳的分量~~~\n~~由正弦定理知由图看出由以上各式得3.运动的合成与分解:在船渡河中，。推广1.当骑自行车的人向正东方向以5m/s的速度行驶时,感觉风从正北方向吹来,当骑自行车的人的速度增加到10m/s时,感觉风从正东北方向吹来.求风对地的速度及的方向.（答案：m/s，方向正东南）V风对地=V风对人+V人对地，得V风对地=m/s，方向正东南2.如图所示,质点P1以v1的速度由A向B作匀速直线运动,同时质点P2以v2的速度由B向C作匀速直线运动,AB=L,ÐABC=a,且为锐角,试确定何时刻t,P1、P2的间距d最短,为多少?（答案：；）解:以A为参照物,vBA=vB地+v地A。B相对A的运动方向和速度的大小如图所示.则B相对A的速度为有正弦定理，当B运动到D时(AD垂直AB)P1、P2的间距d最短,.所需的时间.3.一半径为R的半圆柱体沿水平方向向右以速率为v做匀速运动.在半圆柱体上搁置一根竖直杆,杆与半圆柱体接触为点P，此杆只能沿竖直方向运动,如图所示.求当OP与柱心的连线与竖直方向的夹角为a时,竖直杆运动的速度和加速度.（答案：vtana；）解:(1)取半圆柱体作为参照系.在此参照系中P点做圆周运动,v杆柱的方向沿着圆上P点的切线方向,v杆地的方向竖直向上,因为,矢量图如图a所示.得v杆地=vtana。也可用微元法求.(2)有,因a柱地=0,所以a杆地=a杆柱,而a杆地的方向竖直向下,又a杆柱可分解成切线方向at和法线方向an,矢量图如图b所示,~~~\n~~,所以得到.问题：若圆柱体的加速度为a，则a杆地=？，，a杆地的方向仍在竖直方向上。三．抛体运动1.竖直上抛运动:v=v0-gt,s=v0t-gt2/2.如初速v0=20m/s竖直向上抛出,取g=10m/s2.求经t=3s物体的位移.可用分段解,也可用s=v0t-gt2/2直接求解(15m,方向向下)1.在地面上的同一点分别以v1和v2的初速度先后竖直向上抛出两个可视作质点的小球,第二个小球抛出后经过Dt时间与第一个小球相遇,改变两球抛出的时间间隔,便可改变Dt的值,已知v1