- 534.00 KB
- 2022-07-26 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
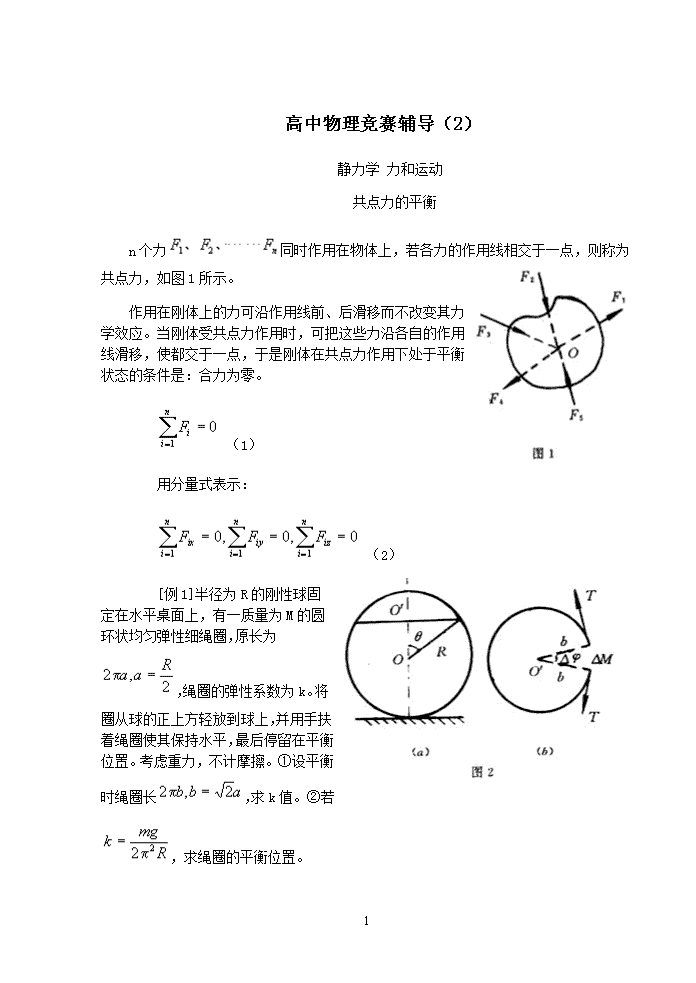
高中物理竞赛辅导(2) 静力学力和运动 共点力的平衡n个力同时作用在物体上,若各力的作用线相交于一点,则称为共点力,如图1所示。作用在刚体上的力可沿作用线前、后滑移而不改变其力学效应。当刚体受共点力作用时,可把这些力沿各自的作用线滑移,使都交于一点,于是刚体在共点力作用下处于平衡状态的条件是:合力为零。 (1) 用分量式表示: (2) [例1]半径为R的刚性球固定在水平桌面上,有一质量为M的圆环状均匀弹性细绳圈,原长为,绳圈的弹性系数为k。将圈从球的正上方轻放到球上,并用手扶着绳圈使其保持水平,最后停留在平衡位置。考虑重力,不计摩擦。①设平衡时绳圈长,求k值。②若,求绳圈的平衡位置。14\n 分析:设平衡时绳圈位于球面上相应于θ角的纬线上。在绳圈上任取一小元段,长为,质量为,今将这元段作为隔离体,侧视图和俯视图分别由图示(a)和(b)表示。 元段受到三个力作用:重力方向竖直向下;球面的支力N方向沿半径R指向球外;两端张力,张力的合力为位于绳圈平面内,指向绳圈中心。这三个力都在经线所在平面内,如图示(c)所示。将它们沿经线的切向和法向分解,则切向力决定绳圈沿球面的运动。 解:(1)由力图(c)知:合张力沿经线切向分力为: 重力沿径线切向分力为: (2-2) 当绳圈在球面上平衡时,即切向合力为零。 (2-3) 由以上三式得 (2-4)14\n 式中 由题设:。把这些数据代入(2-4)式得。于是。 (2)若时,C=2,而。此时(2-4)式变成 tgθ=2sinθ-1,即sinθ+cosθ=sin2θ,平方后得。在的范围内,上式无解,即此时在球面上不存在平衡位置。这时由于k值太小,绳圈在重力作用下,套过球体落在桌面上。 [例2]四个相同的球静止在光滑的球形碗内,它们的中心同在一水平面内,今以另一相同的球放以四球之上。若碗的半径大于球的半径k倍时,则四球将互相分离。试求k值。 分析:设每个球的质量为m,半径为r,下面四个球的相互作用力为N,如图示(a)所示。 又设球形碗的半径为R,O'为球形碗的球心,过下面四球的球心联成的正方形的一条对角线AB作铅直剖面。如图3(b)所示。当系统平衡时,每个球所受的合力为零。由于所有的接触都是光滑的,所以作用在每一个球上的力必通过该球球心。14\n 上面的一个球在平衡时,其重力与下面四个球对它的支力相平衡。由于分布是对称的,它们之间的相互作用力N,大小相等以表示,方向均与铅垂线成角。 下面四个球,由于分布的对称性,每个球受另外两个球的合作用力是一个水平力,方向垂直于碗的轴线。除水平力外,还有重力mg,碗对球的支力,上球的压力,这四个力都通过该球球心,并位于同一平面内,如图3(b)所示。 解:以A球为隔离体,把它所受的力分解为水平分量和垂直分量。 以上球为隔离体 联立以上三式解出:。 当下面四球之间的相互作用为零,即N=0,得。如时,下面四球将互相分离。又 由图形(b)看出。 代入(2-4)式得。 此时下面的四个球互相分离,。 2.共面力的平衡14\n 作用在刚体上的所有力都位于同一平面,这些力就叫做共面力。设共面力所在的平面是xy平面,刚体在平面力作用下平衡的条件是:合力为零和对任一点所有力矩之和为零,即 (3) [例3]有6个完全相同的刚性长薄片,其两端下方各有一个小突起,薄片及突起的质量忽略不。将此6个薄片架在一只水平的碗上,使每个薄片一端的小突起恰好落在碗口上,另一端小突起位于其下方薄片的正中,由正上方俯视如图表(a)所示。若将一质量为m的质点放置在薄片上一点,这一点与此薄片中点的距离等于它与小突起的距离。求:薄片中点所受的(由另一薄片的小突起所施的)压力。 分析:设对中点所施的压力为P,方向向下;将为隔离体,以为支点,可看出所受的压力为;同理将为隔离体,以为支点可得所受的压力考虑薄片,以为支点得所受的压力是。14\n 解:考虑薄片,以为支点的力矩平衡方程, 解出:。 [例4]一锁链由2n个相同的链环组成,每两个链环间的接触是光滑的,锁链两端分别在一不光滑的水平铁丝上滑动,它们的摩擦系数μ。证明:当锁链在铁丝上相对静止时,末个链环与铅垂线交角为, 分析:如图5(a)所示,由于对称性,锁链两端与铁丝接触点0,O'的垂直作用力N=nmg,m是每个链环的质量。铁丝对锁链端点的摩擦力。 解:设链环的长为l,重心在其中心,取右端第一个链环为隔离体,当它平衡时对通过A点垂直于纸面的轴的合力矩为零,以N、f之值代入,即可解得:。 3、物体平衡的种类 下面讨论物体在重力和支力作用下所处的各种平衡状态,图6表示放在凹 面底端、凸面顶端和平面上的小球,它们所受的重力和支力等值反向,都处在平衡位置。14\n 由于某种因素,小球稍稍偏离平衡位置,在凹面底部的小球重心升高,重力势能增大,重力mg和支力N不再保持平衡,合力指向原来的平衡位置,小球会恢复平衡,这种平衡叫做稳定平衡。位于凸面端的小球稍微偏离平衡位置后,重心降低,重力势能减少,重力和支力也不再平衡,合力指向远离原来平衡位置的方向,这种平衡叫做不稳定平衡。平面上的小球偏离原来位置后,重心的高度和重力势能不变,小球仍保持平衡,这种平衡叫做随遇平衡。 [例5]任意横截面的柱体A静止在固定柱体A'上面,如图7(a)所示。G是A的重心,G到接触点的距离是h,D、D'是这两个截面接触点的曲率中心;P、P'是相应的曲率半径,求:h、p、p'满足什么关系时,A处于稳定平衡状态?并加以讨论。 分析:当A稍微偏离平衡位置,接触点相对于D'转过角度,而DG与DD'相交θ角,如图7(b)所示,和θ都是很小的角度,显然PQ=P'Q'。设A的质量为m,由图7(b)知质心G到D'的垂直距离H=(P+P')COS-(p-h)=COS(θ+)。若以D'为零势能的参考点,则当A稍微偏离平衡位置时,其重力势能为 (5-2) 当A在平衡位置时,重力势能是(5-3) 解:由于和θ是小量,因此,(5-2)可写作。 。(5-4)14\n 于是,势能增加,相应于稳定平衡;,势能减少,相应于不稳定平衡。 因此 即稳定平衡的条件为(5-5) 不稳定平衡条件为(5-6) 如果上面物体A的接触面为平面,于是稳定平衡条件为,否则是不稳定平衡。如果物体A放置在平面上,则,稳定平衡的条件为,否则就是不稳定平衡。 4、运动定律的应用 应用牛顿运动定律解决具体问题时,首先要明确讨论的是哪一个(或哪一些)物体的运动,画出隔离体力图。其次要讨论物体的运动情况特别要注意加速度,因为它起着将运动定律和运动学联结起来的作用。对隔离体分析了受力情况和运动情况后,就可列出矢量式,但要求出结果还必须建立坐标系,写出运动方程的分量式。 质点动力学问题大致分成两类:(1)已知质点的运动情况,求其它物体施于该质点的作用力;(2)已知其它物体施于质点的作用力,求质点运动情况。 [例6]图8(a)所示。两个木块A和B,质量分别为14\n,紧挨着并排放在水平桌面上,A、B间的接触面垂直于纸面且与水平成θ角,A、B间接触面是光滑的,但它们与桌面存在摩擦,静摩擦系数和滑动摩擦系数均为μ,开始时A、B都静止,现施一水平推力F于A,要使A、B向右加速运动且A、B之间不发生相对滑动。则(1)μ的数值应满足什么条件?(2)推力F的最大值不能超过多少?(只考虑平动)? 分析:A、B的受力图如图8(b)所示。由于A、B间接触面是光滑的,它们之间相互作用力N垂直于接触面。 解:(1)若A、B之间不发生相对滑动,则A在竖直方向的加速度为零,即。(6-1) B以加速度a>0向右运动 联立以上三式,解出: (2)在已满足(6-4)式的情况下,A、B的水平加速度均为a,于是 由A: 由B: 解出A、B间不发生相对滑动的 [例7]固定在粗糙桌面上的三棱柱C,质量千克,滑块A、B质量千克,14\n千克。定滑轮质量不计联接A、B的轻绳不可伸长。开始时使A、B、C都处于静止状态,且滑轮两边轻绳伸直,今以F=26.5牛的水平推力作用于C,同时释放A、B、C。若C沿桌面向左滑行,其加速度,B相对于桌面无水平方向位移(绳子一直是绷紧的)。求:C与桌面间的摩擦系数μ。已知:。 分析:这是一个具有相对运动的动力学问题,以桌面为静止参照物,三棱柱C为运动参照系,则滑块相对于桌面的加速度(绝对加速度)a,等于滑块相对于三棱柱的加速度(相对加速度)a'与三棱柱相对于桌面的加速度(牵连加速度)a0之和。 。 由题意:滑块B相对于桌面无水平方向位移,所以B的绝对加速度沿水平x方向的分量为零。 , 于是滑块的相对加速度的大小。 由于绳子不可伸长,又是绷紧的,所以A、B的相对加速度的数值是相等的但方向不同,由图9(b)所示。 滑块A的绝对加速度的两个分量: 滑块B的绝对加速度的两个分量:14\n 解:对于A、B、C组成的系统,在x方向受到外力是推力F和摩擦力f。于是:将有关数据代入,解出f=10牛。 系统在y方向受到的外力是:桌面作用于C的支持力N,方向+y;A、B、C所受的重力为,方向-y,所以 将有关数据代入,得N=93牛。 最后得摩擦系数。 习题 1.质量为m,半径为R的球放在竖直墙和板AB之间。A端用绞链固定在墙上,B端用水平细绳拉住,如图10所示。板长l,和墙夹角a。不计摩擦及板的质量。求:(1)绳的拉力T;(2)角a为何值时,T有最小值。 2.用一个水平放置的半径为R的圆柱形光滑槽面,其轴线通过O点,槽内放着两个半径均为r的光滑圆柱体A、B,如图11所示。质量分别为,且r=R/3,求:圆柱体A、B平衡时,OA线与竖直线间的夹角a是多少?14\n 3.一条轻绳跨过同一高度上的两轻滑轮。两端分别栓上质量为4千克和2千克的物体,滑轮间的一段绳上挂第三个物体M,如图12所示。试问:M的质量小于何值时,三个物体平衡将被破坏?不考虑滑轮大小和摩擦。(千克) 4.底边长为a,高度为b的长方形匀质的物块置于斜面上,斜面和物体之间的静摩擦系数为μ,斜面的倾角为θ,当θ足够小时,物块静止在斜面上(如图13)。如逐渐将倾角增大,当θ取某个临界值时,物块或将开始滑动,或将翻倒。试说明在什么条件下出现的是滑动;在什么条件下出现的是翻倒。 (当,木块滑动;,木块翻倒) 5.两个质量分别为的小环能沿着一轻绳光滑地滑动,绳的两端固定于直杆的两端,杆与水平线成角度θ。在此杆上又套一轻小环,绳穿过轻环并使在其两边(如图14)。设环与直杆的接触是光滑的,当系统平衡时,直杆与轻环两边的绳夹角。试证: 。14\n 6.在互相垂直的斜面上放置一匀质杆AB,如图15示。设各接触面的摩擦角均为,求平衡时杆AB与与斜面AO的交角θ。已知斜面BO和水平面交角a。 7.两个相同的等腰楔子,质量均为M,顶角为2a,把它们的底面靠在一起,放置于粗糙水平桌面上,底面与桌面之间的静摩擦系数为μ,底面边长为l,把一个质量为m,半径为r的光滑球放置其间。由图16所示。试证:平衡的必要条件是:。 8.一个熟鸡蛋的圆、尖两端的曲率半径分别为a、b,且长轴的长度为c,证明:蛋尖的一端可以在不光滑的水平面上稳定直立。如图17所示。并求碗的半径r。 9.A、B、C三物体,质量分别为,A、B叠放在光滑的水平桌面上(如图18),A、B之间的静摩擦系数为μ,不计绳与滑轮之间的摩擦及质量。整个系统由静止释放。讨论:A与B不发生相对运动的条件。 10.如图19所示,在水平光滑的平面上,质量分别为14\n的两个质点,用轻质弹簧联在一起,并以长为的细线拴在轴O上,均以角速度ω绕轴O作匀速圆周运动。两球间的距离。如将线烧断。求:在线刚烧断的瞬间,的加速度。 14