No.31全国高中数学联合竞赛模拟试题 13页

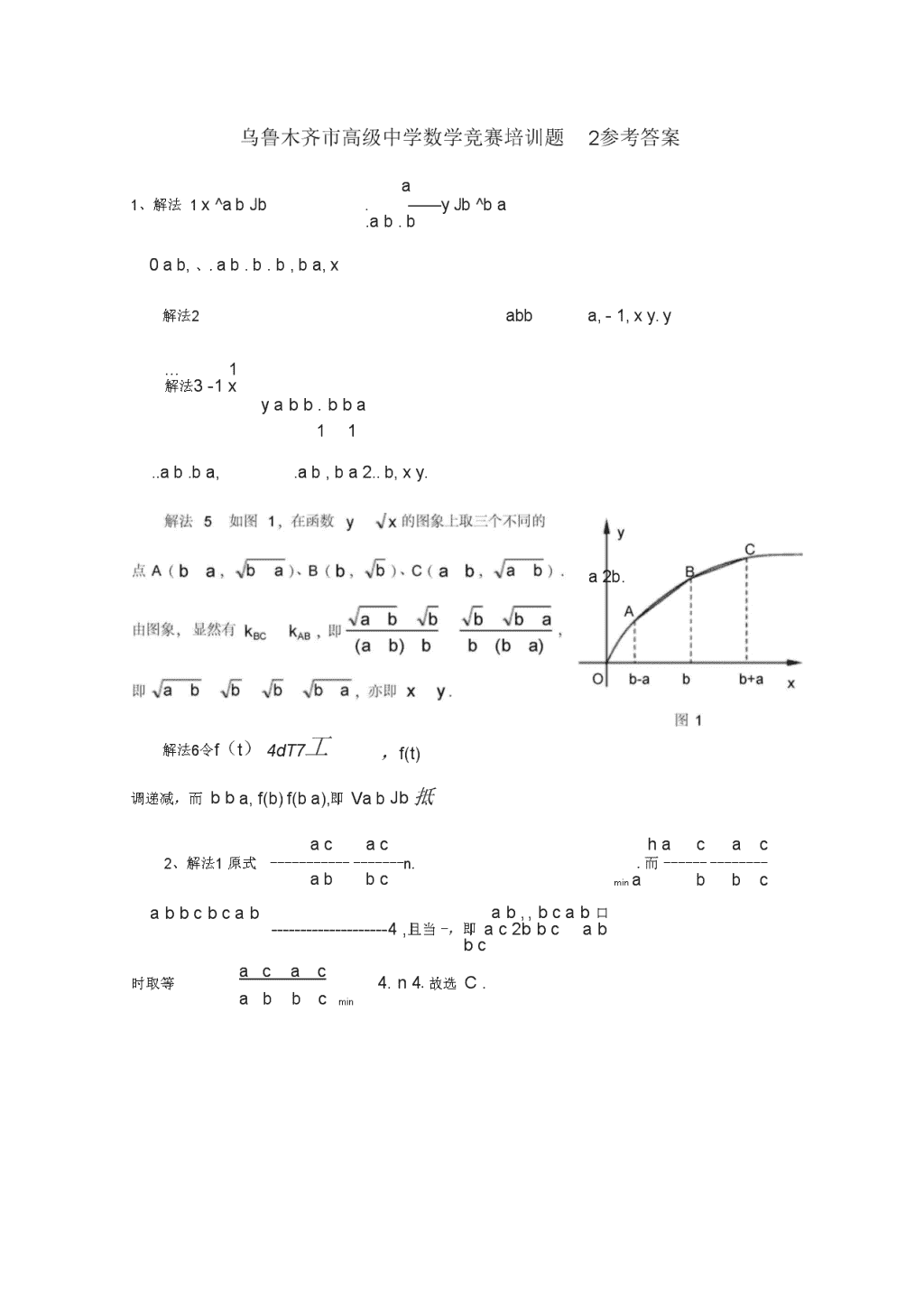
No.31高中数学联赛模拟试卷1、已知0ab,xJabbb,ybbbb—a,则x,y的大小关系是.11n2、设abc,nN,且恒成立，则n的取大值为abbcac，_.,23、对于m1的一切实数m,使不等式2x1m（x1）都成立的实数x的取值范围是sincos4、已知fx10gsinx,0,一，设af,bfvsincos22cf,那么a、b、c的大小关系是sincos2000_5、不等式v4x22V3x的解集是^1999.x22x2.一,，6、函数fxx1的最小值为2x2_.117、若a,b,nR,且abn,则1一1-的取小值是ab8、若3x2xy3y220,贝U8x223y2的最大值是.9、设nN,求|n1949||n19501|n2001|的最小值.1,，―一八f--，则s的整数部分10,,11,10、求s1—pl^L11、圆周上写着红蓝两色的数。已知，每个红色数等于两侧相邻数之和，每个蓝色数等于两侧相邻数之和的一半。证明，所有红色数之和等于0。（俄罗斯）12、设a,b,cR,求证:b2\n（第二届友谊杯”国际数学竞赛题）\n乌鲁木齐市高级中学数学竞赛培训题2参考答案a1、解法1x^abJb.——yJb^ba.ab.b0ab,、.ab.b.b,ba,x解法2abba,-1,xy.y…1yabb.bba解法3-1xa2b.11解法6令f（t）4dT7工..ab.ba,.ab,ba2..b,xy.，f(t)调递减，而bba,f(b)f(ba),即VabJb抵hacac.而minabbcacac2、解法1原式n.abbcbcababbcab,,bcab口4,且当，即ac2bbcabbc时取等acacabbcmin4.n4.故选C.\n解法2abc,ab0,bc0,ac0,已知不等式化为2ac2abbc4,即min故由已知得n4,0,b0,ac0解法44,4,由题意,4.故选minc,0,bc已知不等式可变形为解法53、解法1题设等价于102x1或x212x解法2已知不等式即等式恒成立，由题意,4.故选C.0,—0.于bc4,、r4-^—•比较得ac102x1或x210，所以1x0x211时,4.故选2或＜3m2x102x1或x212x，令f(m)f(m)是m的一次函数，因为2xx211,2).2x1所以f(m)在1,1上的图象恒在m轴的下方1时不\nf(1)f(1)又当2x12x12x11时,f(m)2x2x适合题意,2x2x故x的取值范围是＜32.4、解法1设sincosq.1时，f(m)1x2(x1).3不合题意.x是减函数,f0,则.anan1aan〈ananan1aan$an1d(n2,n,d是公差）.由此,得s1121,3_1_,106、3.3—2_12106.106.21又知s评析.106,3..1061998.、2,106一106111,1061106v1061.1061999...10610611998s1999,1998,1，-6s显然是数列的刖10项的和,直接求和，无法可依.能否用裂项相消法将每项拆成异号的两项之和呢？考虑到--nn11…1、，于是将」变为再放大为这是一道用放缩法”求解不等式问题的好题目。但用放缩法”解题，必须把握好放缩的度”就以此题为例，若将11••213L-161021.12-2-2106,-106:0.106J0612[10J106V1061]2000,就彳导1998s2000,这样就没法确定s到底是1998还是1999了.若做到这里，我们便应考虑到题中的1不作变形，问题就会得到解决.此题来源于高中代数下册（必修）P132第33题：用数学归纳法证明\njn,n1.1992年全国高考三南”试题：证明不等式:1___——2、.n,nN.这两个结论合起来就有■,nJn1I」3L1二2、,n、.nN.此结论就是而s2jn.11、解:将所有红数的和记为SH，所有蓝数白和记为SL,对任意两个a,b,c都有a+c=b或2b(视b为红数还是蓝数而定)。将所有这些等式全部求和，从等式的左边看：每个数都被加被加了两次，所以总和为了两次，所以总和为2(0+Sl)；从等式的右边看：每个红数都被加了一次，每个蓝数都SH+2Sl,因此Sh+2sL=2(Sh+Sl),故Sh=0。12、证明设bcx,cay,ac1xyzx,y,z0.2.2,2.2①,ababaybx————0,xyxyxyxyabcabcabc，即xyz2abc20,0,xy.xy解法4原问题等价于比较JabJBF与2